Квадрат теңсіздік

Презентация қосу

Квадрат теңсіздік.
Квадрат теңсіздікті квадраттық
функцияның графигі арқылы шешу
• Сабақтың мақсаттары:
Білімділік: Квадрат теңсіздік ұғымымен
таныстыру,квадрат теңсіздіктерді графиктік тәсілмен
шешуді үйрету.
• Дамытушылық:
• Ой - өрісін дамыту, ойлау қабілетін арттыру,
теориялық білімін практикада қолдана білу,өз
бетімен жұмыс жасай білу дағдысын қалыптастыру.
• Тәрбиелілік:
• Шапшаңдыққа, іздемпаздыққа, тиянақтылыққа,
ұқыптылыққа, ұжымдық ауызбіршілікке тәрбиелеу.
• Сабақтың міндеттері:
• квадраттық функцияның графигін
салуды,графиктердің орналасуын, квадраттық
функцияның қасиеттерін қайталау;
• квадраттық функцияның графигін схемалық түрде
салу білуін дамытуды жалғастыру;
• квадраттық теңсіздіктерді шеше білу алгоритмін
қалыптастыру;
• квадраттық теңсіздіктерді графиктік тәсілмен шешуге
дағдыландыру;
• материалды игеру деңгейін алғашқы тексеру;
• оқушылардың шығармашылық ойлау қабілетін
дамытуға,талдауға,жүйелеуге,өз ойын сауатты жеткізуге
ықпал ету;
• 1.Теориялық бөлім
• а) Квадраттық функцияның графигі
• Квадраттық функцияның графигі қандай қисық?
• Квадраттық функцияның графигі - парабола
• а>0 болғанда, парабола тармақтары қалай
бағытталады?
• а>0 болғанда, парабола тармақтары
жоғары бағытталады
• а<0 болғанда, парабола тармақтары қалай
бағытталады?
• а<0 болғанда, парабола тармақтары төмен
бағытталады.
• D>0 болғанда, параболаның абсцисса
осімен орналасуы туралы не айтуға
болады?
• D>0 болғанда, парабола абсцисса осімен
екі нүктеде қиылысады.
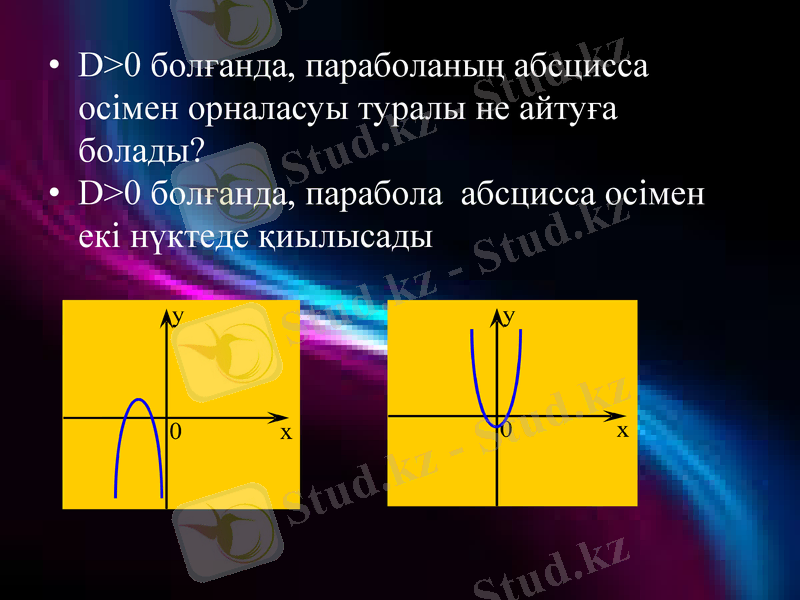
• D>0 болғанда, параболаның абсцисса
осімен орналасуы туралы не айтуға
болады?
• D>0 болғанда, парабола абсцисса осімен
екі нүктеде қиылысады
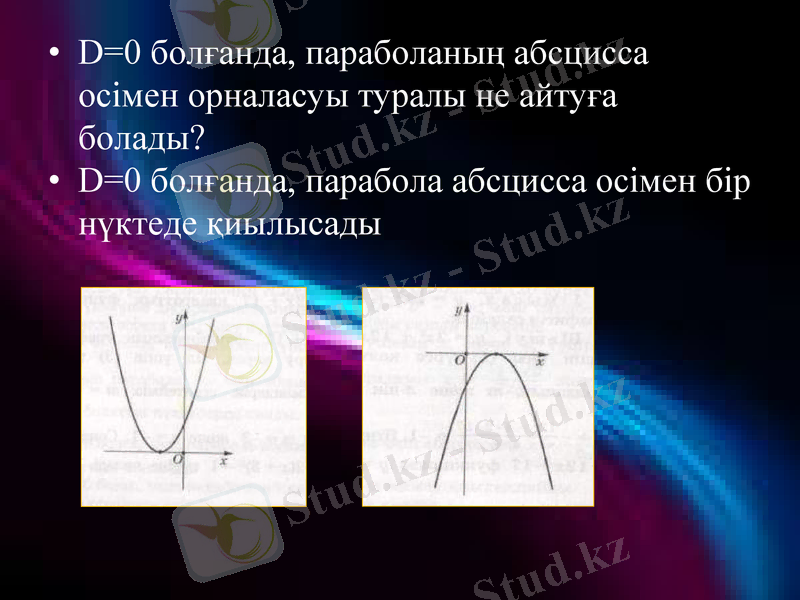
• D=0 болғанда, параболаның абсцисса
осімен орналасуы туралы не айтуға
болады?
• D=0 болғанда, парабола абсцисса осімен
бір нүктеде қиылысады
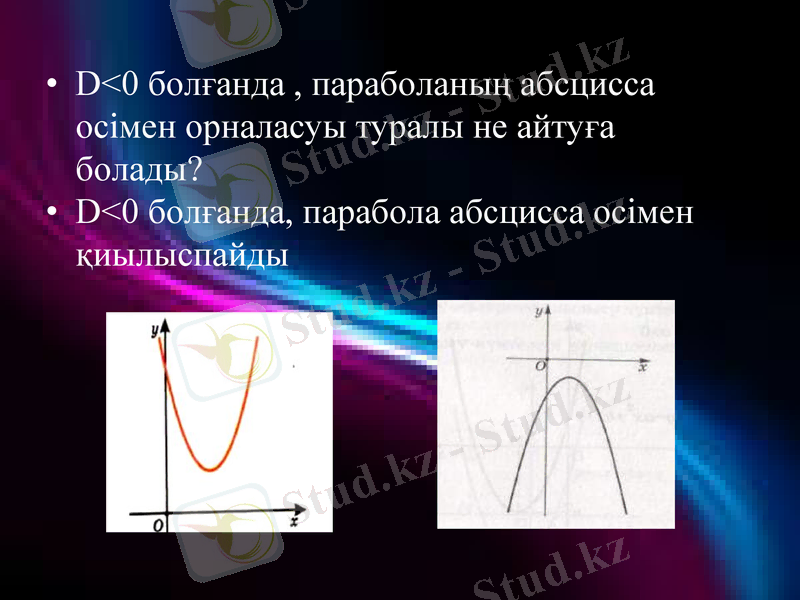
• D<0 болғанда , параболаның абсцисса
осімен орналасуы туралы не айтуға
болады?
• D<0 болғанда, парабола абсцисса осімен
қиылыспайды
квадраттық теңсіздіктерді шешу
алгоритмін қалыптастыру
•

мұнда a, b, c нақты сандар және а≠0 а>0 D>0
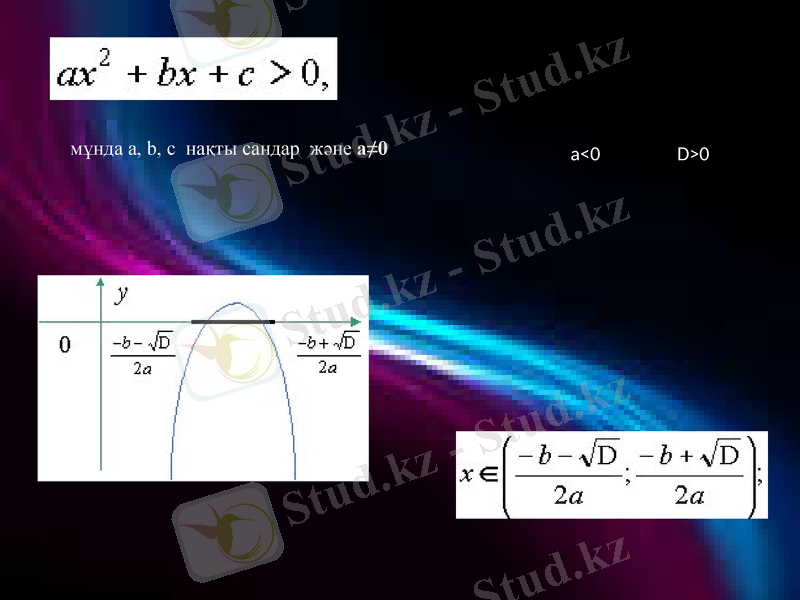
мұнда a, b, c нақты сандар және а≠0 а<0 D>0
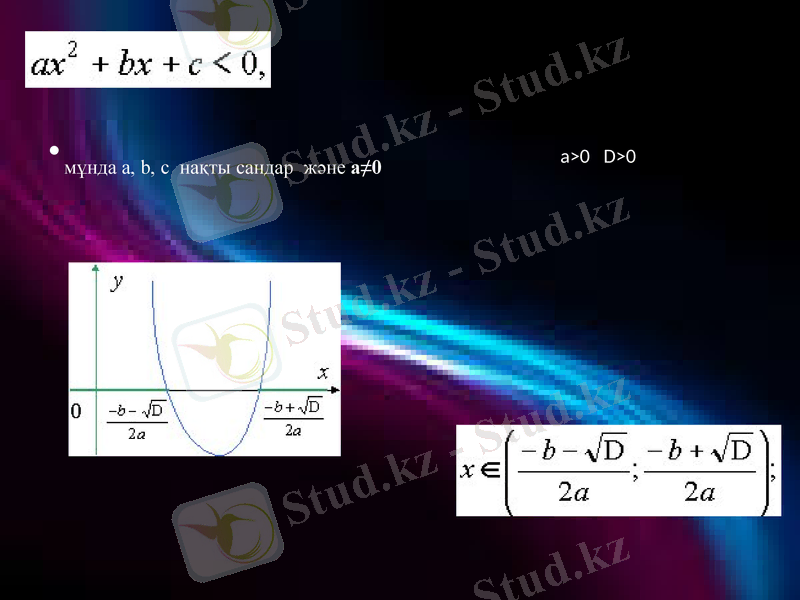
• мұнда a, b, c нақты сандар және а≠0 a>0 D>0
мұнда a, b, c нақты сандар және а≠0 а<0 D>0
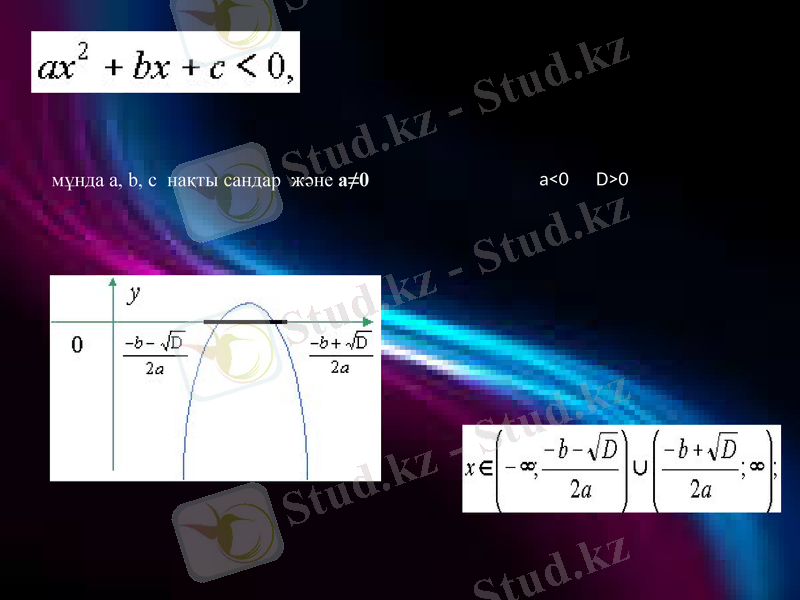
мұнда a, b, c нақты сандар және а≠0 а>0 D<0

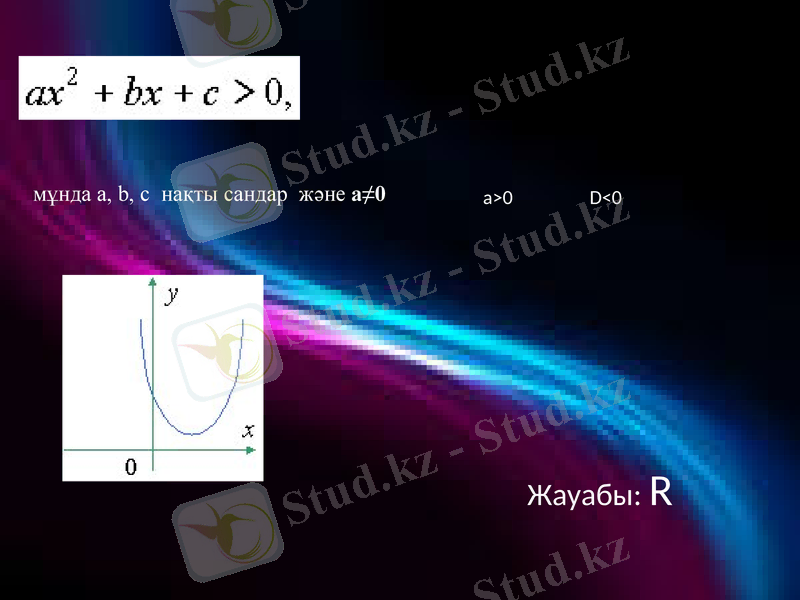
Жауабы: R
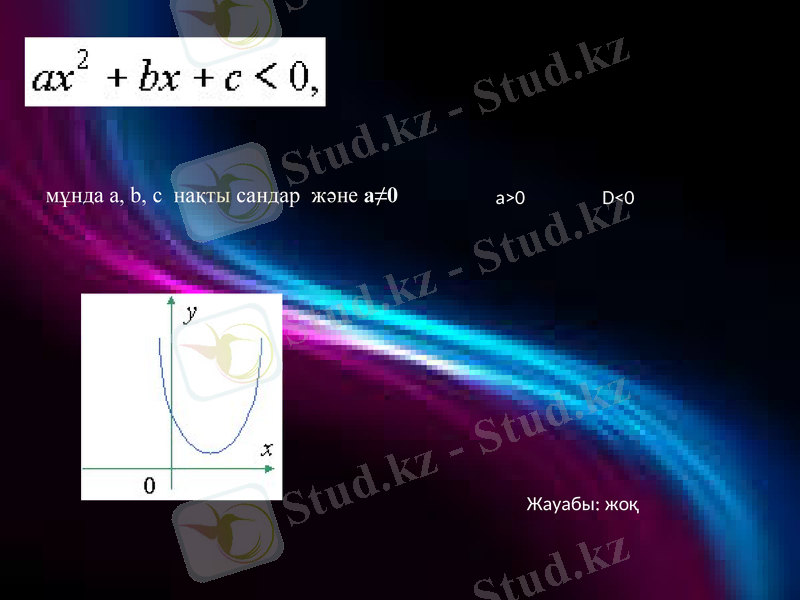
мұнда a, b, c нақты сандар және а≠0 а>0 D<0

Жауабы: жоқ
• квадрат теңсіздігін шешудің алгоритмі.
•
1) у= ах²+bх+с функциясын жазамыз .
2) Функцияның нөлдерін табамыз.
3) а санының таңбасына қарап функцияның
схемалық графигін саламыз.
4) График бойынша теңсіздікті
қанағаттандыратын аралықты анықтаймыз.
• Практикалық бөлім
• №42.
• 1)x2-5x+4<0
• x2-5x+4=0
• Х1=1 х2=4

Жауабы: ( 1;4)
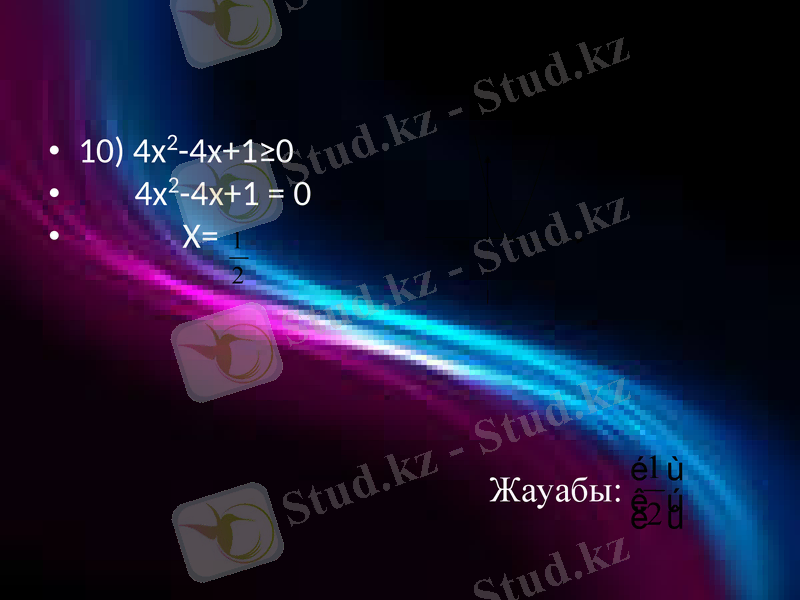
• 10) 4x2-4x+1≥0
• 4x2-4x+1 = 0
• Х=

Жауабы:
НАЗАРЛАРЫҢЫЗҒА
РАХМЕТ
Орындаған:

Ұқсас жұмыстар

Квадраттық функцияны интервалдар әдісімен шешу, әдістің мәнін түсіну

Мектеп математикасындағы квадраттық теңдеулерді шешу жолдары

Интервалдар әдісі

Модуль белгісімен алынған теңсіздіктер

Квадрат теңсіздіктер

Квадрат үшмүшені көбейткіштерге жіктеуге есептер шығару

Рационал теңсіздік

Грек математикасының Римдік дамуы

Тілді қалай өзгертем

Әлеуметтік теңсіздік көрсеткіштері

Пәндер