Математиканың қолданылуы: пішіндер, Пик теоремасы, есептер мен ПИСА/ҰБТ тапсырмалары



Аралас формулла

Мені қоршаған ортадағы математика

Математика-ең керемет сала. Өкінішке орай атын ұмытып тұрмын, бірақ сол адам былай депті: «Математиканың тілі бар, ол - Формула» деген.
Алла Тағала Жер бетін алты күнде жаратқан «Мен үшін Алла Жерді былай айтқанда есептеп жаратты десек артық кетпес. Жер планетасы-математикадан «Шар», яғни «сфера». Орбитаның өзі - «шеңбер».
Өз өмірімізге тоқталсақ, жан-жағымыз математика. мысалы параллелепипед тәрізді ғимараттар, шаршы тәріздес ғимараттар. Тік төртбұрышты телефон - смартфондар. Ғарышқа көз тастасақ, жұлдыз да коордианаталық түзулерге ұқсайды. Тіктөртбұрышты кітаптар, шар тәріздес доптар, шеңбер тәрізді обручтар, сақина, білезіктер.
Көп салалар математикамен байланысты және математикадан бастау алатыны да бар. Мысалы, биология, химия, тарих, география, биохимия, т. б математикамен байланысты, «математикасыз өмір сүре алмайды» деуге де болады. Ал арифметика, алгебра және де информатика тәріздес салалар математикадан бастау алады.
Математика - салалардың саласы.

Пик теоремасы
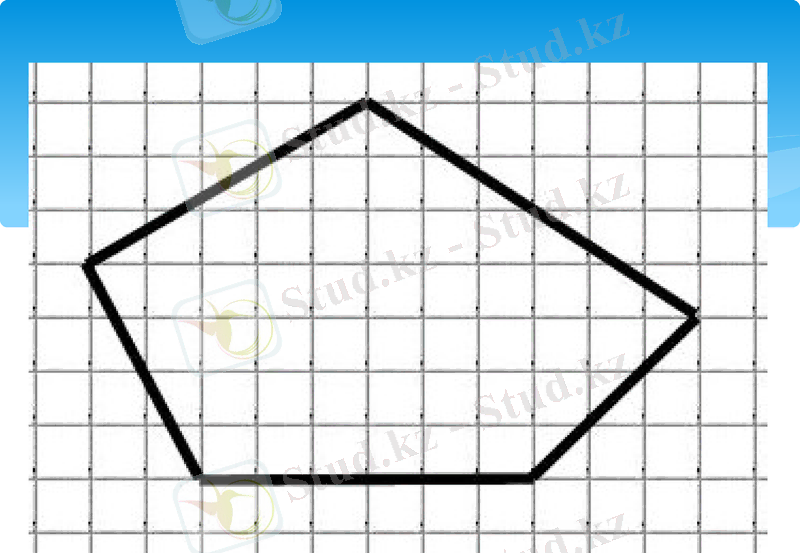
Пик теоремасы бойынша көпбұрыштың ауданы :
Г : 2 + В - 1-ге тең, мұндағы
Г - көпбұрыш шекарасындағы торкөздер түйінінің саны
В - көпбұрыштың ішіндегі торкөздер түйінінің саны
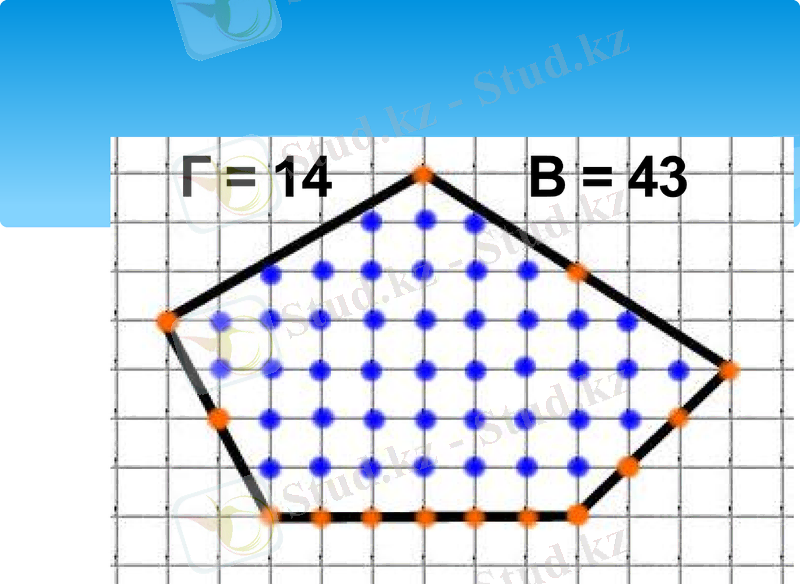

Пик теоремасы бойынша көпбұрыштың ауданы :
Г : 2 + В - 1-ге тең, мұндағы
Г - көпбұрыш шекарасындағы торкөздер түйінінің саны
В - көпбұрыштың ішіндегі торкөздер түйінінің саны
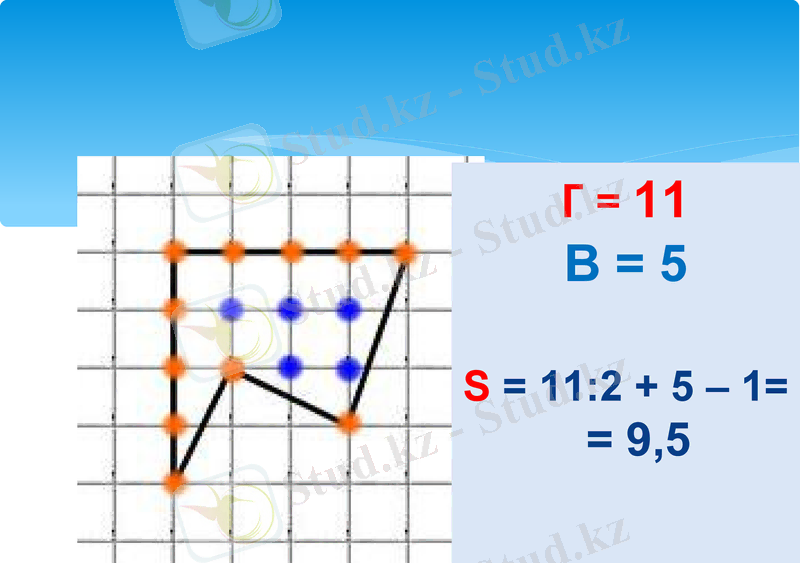
Г = 11
В = 5
S = 11:2 + 5 - 1= = 9, 5

Тірек сандар көмегімен тез көбейту тәсілі

48·53 -2 +3 48 53
50·(48+3) +(-2·3) =50·51-6=2550-6 =2544

Математикалық басқатырғылар мақсаты: жұмыстың нәтижесін көз алдымызға елестете отырып, нәтижеге тез қол жеткізу.

1 - тапсырма
Осы үшбұрышты
3 шеңберді қозғай отырып төңкеріп қою керек.
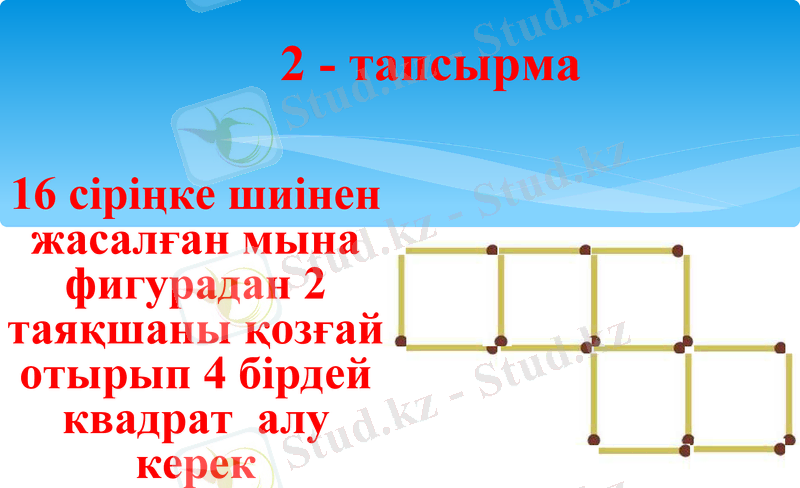
2 - тапсырма
16 сіріңке шиінен жасалған мына фигурадан 2 таяқшаны қозғай отырып 4 бірдей квадрат алу керек

3 - тапсырма
6 қарандаштан
4 бірдей үшбұрыш жасау керек.

PISA зерттеулеріндегі
математикалық сауаттылыққа
берілген есептер

АЛМА АҒАШТАР
Фермер бау-бақшада, суретте көрсетілгендегідей, төртбұрыш формасында алма отырғызады. Алмаларды желден сақтау үшін шет- шетінен қылқан жапырақты ағаштар (хвойные деревья) отырғызады.
Бірнеше п мағыналары үшін төмендегі суретте отырғызылған алма ағаштары мен қылқан жапырақгы ағаштардың сызбанұсқасы берілген,
n - отырғызылған алма ағаштары қатарларының мөлшері. Бұл тізбекті
n-ның кез-келген санына дейін жалғастыруға болады.

Сұрақ : АЛМА АҒАШТАР
Жоғарыда қарастырылған алма ағаштарының саны мен қылқан жапырақты ағаштар санының тізбегі төменде көрсетілген ретпен есептелінеді:
алма ағаштарының саны = n 2,
қылқан жапырақты ағаштар саны = 8 n,
n - алма ағаштары қатарының саны.
n -ның қай мәнінде алма ағаштарының саны шет-шетінен отырғызылған қылқан жапырақты ағаштардың санымен тең болады? Шешімін жазыңыз.

Сұрақ : АЛМА АҒАШТАР
Фермер өз аумағындағы алма ағаштарының қатарын ақырындап көбейтуді ойластыруда деп болжайық. Осы кезекге отырғызылған қай ағаштың саны тезірек кобейеді: алма ағаштардың ба әлде қылқан жапырақты ағаштардың ба?
Өз жауабыңыздың түсіндіріп жазыңыз.

ТҰРҒЫН ҮЙ
Суретте шатыры пирамида пішіндес тұрғын үй бейнеленген. Төменде оқушылар жасаған тұрғын үй шатырының моделі және кейбір кескіндердің ұзындығы көрсетілген.
Бұл модельде шатырдың етегі - АВСD квадрат. Шатыр сүйенетін тіреуіштер, ЕFGHKLMN тікбұрышты параллелепипедтің пішіні бар бетон блогының қабырғалары болып табылады. Е - АТ қабырғасының орта қыры, Ғ-ВТ қабырғасының ортасы, G - СТ қабырғасының ортасы, Н - DТ қабырғасының ортасы. Пирамданың барлық қырлары 12 м тең.
Сұрақ 25: ТҰРҒЫН ҮЙ
АВСD квадратының шатыр етегінің ауданын табыңыздар. АВСD квадратының шатыр етегінің ауданы =м2.
Сұрак 26: ТҰРҒЫН ҮЙ
ЕҒ-кескінінің ұзындығын бетон блогының келденең жағынан табыңдар.
ЕҒ-кескінінің ұзындығы = м.


ҰБТ - да тригонометриялық теңдеулер, теңсіздіктер және олардың жүйелерінің шешімдерін табудың тиімді тәсілдері
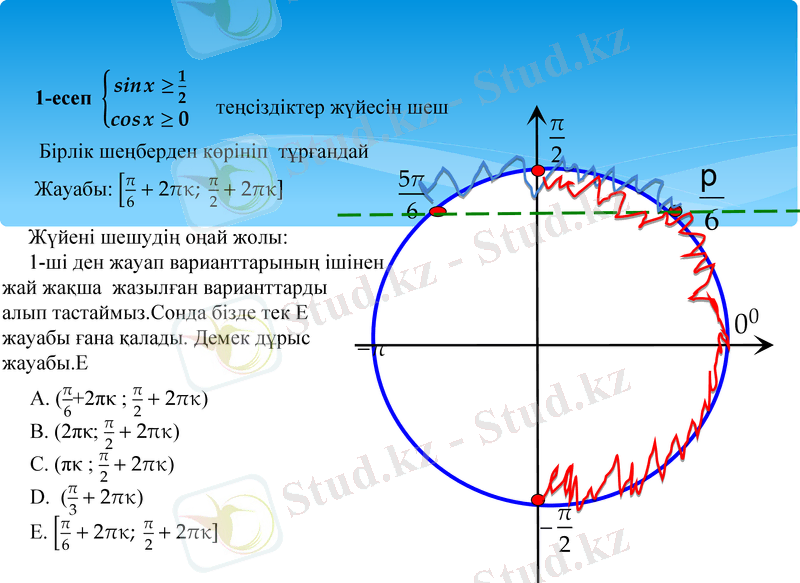
Жүйені шешудің оңай жолы:
1-ші ден жауап варианттарының ішінен
жай жақша жазылған варианттарды
алып тастаймыз. Сонда бізде тек Е
жауабы ғана қалады. Демек дұрыс
жауабы. Е
теңсіздіктер жүйесін шеш
Бірлік шеңберден көрініп тұрғандай
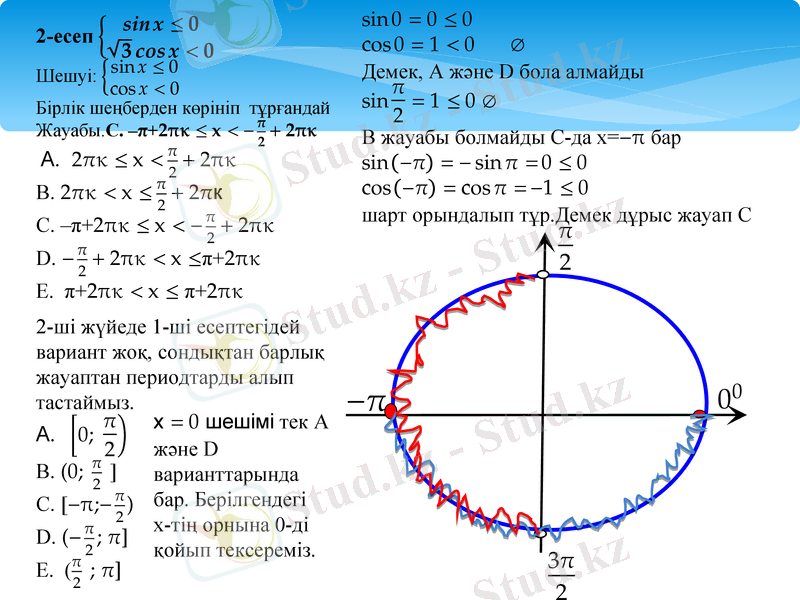
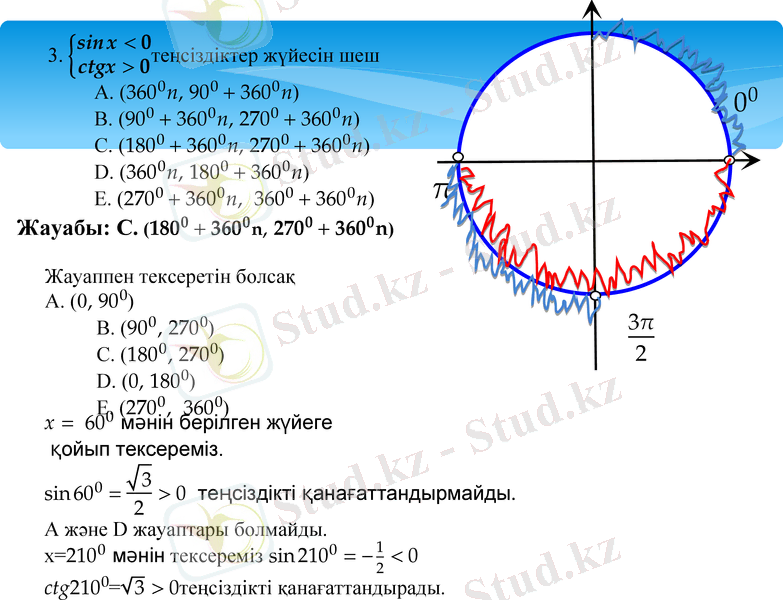



Шарттарын қанағаттандыратын шешімін табайық.
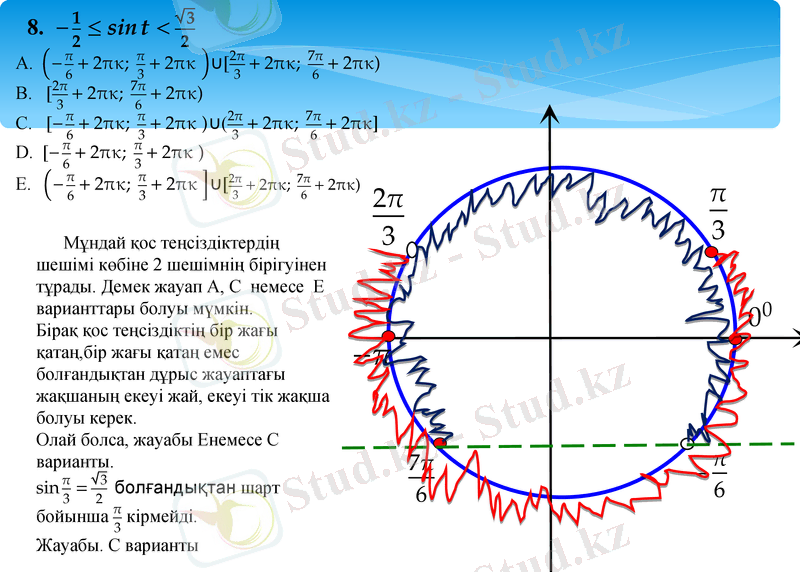

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz