Көпмүшені бірмүшеге бөлу

№202 орта мектеп

Пәні: Алгебра

Тақырыбы: Бірмүше және көпмүшеге

есептер шығару

Сыныбы: 7 “ә”

Пән мұғалімі: Нұрылдаева Райхан

2010-2011 оқу жылы

Сабақтың тақырыбы: Бірмүше және көпмүшеге

есептер шығару.

Білімділік: Оқушылардың бірмүше, бірмүшенің стандарт

түрі, көпмүше және оларға амалдар қолдану, көпмүшені

көбейткіштерге жіктеу жөнінде алған білімдерін тереңдету.

Дамытушылық:

Ой - өрісін дамыту, ойлау қабілетін арттыру, теориялық

білімін практикада қолдан білу дағдысын қалыптастыру.

Тәрбиелік: Шапшаңдыққа, ізденімпаздыққа, тиянақтылыққа,

ұқыптылыққа баулу, ұжымдық ауызбіршілікке тәрбиелеу.

Сабақтың түрі: Аралас сабақ.

Сабақтың әдісі: Топпен жұмыс,

Сабақтың көрнекілігі: Интерактивті тақта, электрондық

оқулық, компьютер, үлестірмелі топтамалар.

Сабақтың барысы:

І. Ұйымдастыру кезеңі:

Оқушылардың сабаққа қатысуын тексеру, үш топқа бөліп отырғызу, назарын сабаққа аудару, сабақтың мақсат, міндеттерін түсіндіру.

ІІ. Үй тапсырмасын тексеру.

ІІІ. Жаңа сабақ.

ІV. Қорытынды:

Бағалау.

Үйге тапсырма беру.

Бірмүше

Анықтама. Санды және әріпті көбейткіштер мен олардың дәрежелерінің көбейтіндісі бірмүше деп аталады.

Мысалы:

5, 9 санды көбейткіштері - бірмүшенің

коэффициенттері,

a, b, c, m, k әріпті өрнектері -

айнымалылар

Айнымалылардың барлық дәреже көрсеткіштерінің қосындысы бірмүшенің дәрежесі деп аталады.

Мысалы:

бірмүшесінің дәрежесі

2+3+1=6

бірмүшесінің дәрежесі

3+2=5

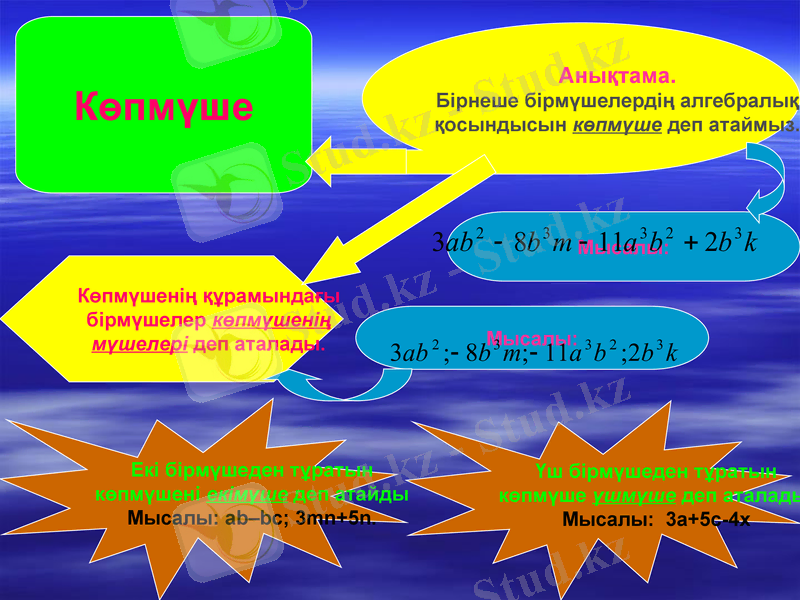
Көпмүше

Анықтама.

Бірнеше бірмүшелердің алгебралық

қосындысын көпмүше деп атаймыз.

Мысалы:

Көпмүшенің құрамындағы

бірмүшелер көпмүшенің

мүшелері деп аталады.

Мысалы:

Екі бірмүшеден тұратын

көпмүшені екімүше деп атайды

Мысалы: аb-bc; 3mn+5n.

Үш бірмүшеден тұратын

көпмүше үшмүше деп аталады.

Мысалы: 3а+5с-4х

Көпмүшеге амалдар қолдану.

Көпмүшелерді

қосу үшін

оның барлық

мүшелерін өз

таңбаларымен

тізбектеп

жазып, ұқсас

мүшелерді

біріктіру керек.

Көпмүшелерді қосу амалы:

Бір көпмүшеден

екінші көпмүшені

азайту үшін

азайғышқа

қарама-қарсы

таңбамен

алынған азайт-

қышты қосса

жеткілікті.

Көпмүшені

бірмүшеге көбейту

үшін бірмүшені

көпмүшенің әрбір

мүшесіне көбейтіп,

шыққан

көбейтінділерді

қосу керек.

Көпмүшені

бірмүшеге бөлу

үшін көпмүшенің

әрбір мүшесін

берілген

бірмүшеге

бөліп, шыққан

нәтижелерді

қосу керек.

Көпмүшелерді

азайту амалы:

Көпмүшелерді

көбейту амалы:

Көпмүшелерді

бөлу амалы:

Көпмүшені көбейткіштерге жіктеу

1. Ортақ көбейткішті

жақшаның сыртына шығару.

ортақ көбейткішті табу;

ортақ көбейткішті

жақшаның сыртына шығару.

Мысалы: 2ху - 3хz + px =

x ∙ (2y - 3z + p)

2. Топтау тәсілі:

1. көпмүшенің мүшелерін ортақ

көбейткіштері бірмүше

немесе көпмүше түрінде болатын

топтарға біріктіру;

2. ортақ көбейткішті

жақшаның алдына шығару.

Мысалы: 24mn+35p -20pn-42m =

(24mn-42m ) +(35p -20pn) =

6m(4n-7m) +5p(7m-4n) =

(4n-7m) (6m-5p)

3. Жаңа қосымша мүшелер енгізу тәсілі:

Бұл тәсілдің негізгі мақсаты-берілген

көпмүшені мүшелер саны

артық басқа көпмүшемен алмастыру.

Мұндай алмастыру шыққан көпмүшеге

топтау тәсілін қолдану үшін жасалады.

Мысалы: a +7a+12 =a +3a+4a+12=

a(a+3) +4(a+3) =(a+3) (a+4)

Бірмүшені стандарт түрінде жазу: ∙

Көбейтуді орындау: ∙

Дәрежеге келтіріп, мәнін табу:,

мұндағы х =, у = -1, z = 4

Бөлуді орындау: :

Теңдіктегі * орнына дұрыс теңдік шығу үшін, бірмүшені жазу:

І. Топ.

Ұқсас мүшелерді біріктіру:

2) Көпмүшелерді қосу:

3) Көпмүшелерді азайту:

4) Көпмүшелерді көбейту:

Көпмүшелерді бөлу: : (3х) + :

6) Көпмүшенің мәнін табу:,

мұндағы х = 2

ІІ. Топ.

Жақшаны ашу: 4ху

2) Теңдеуді шешу: ( х + 1 ) ( х + 4 ) - = 0

Көбейткішке жіктеу: + 7у - 45у - 15

Тиімді тәсілмен шешу: 0, 7 ∙ 2, 7 - 1, 4 ∙ 0, 7 + 0, 3 ∙

2, 7 - 1, 4 ∙ 0, 3

5) Көпмүшені бірмүшеге бөлу:

ІІІ. Топ.

Ұқсас жұмыстар

Гүлге қонған көбелек ойыны

“Бірмүше және көпмүше” тарауын қайталау

Көпмүшені түрлендіру

Критериалды бағалаудың маңызы

Бірмүшелер Теориядан қасиеті

Бүтін өрнекті көпмүшеге түрлендіру

Жоғары дәрежелі теңдеулерді шешу

Жоғары дәрежелі теңдеулер

Көпмүше және оның стандартты түрі

Көпмүшелерді қосу және азайту ережелері қанд

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz