Қарапайым тригонометриялық теңдеулерді шешу әдістері: деңгейлеп оқыту сабақ жоспары

№1 орта мектебі

Тақырыбы:

Тригонометриялық теңдеулерді

шешудің тәсілдірі

математика пән мұғалімі: Б. А. Кудинова

Мақсаты

Оқушылардың қарапайым тригонометриялық теңдеулердің түбірлерін анықтау механизмін түсінуін және оны меңгеруін қалыптастыру арқылы, алған біліктерін тригонометриялық теңдеулерді шешу барысында қолдана білу бейімділіктерін қалыптастыру.

Әдісі: Деңгейлеп оқыту технологиясы

Түрі: Біліктілік пен дағдыны игеру және қалыптастыру сабағы

Сабақ құрылымы:

І. Оқушылық деңгей;

ІІ. Алгоритімдік деңгей;

ІІІ. Эвристикалық деңгей;

IV. Шығармашылық деңгей.

І. Оқушылық деңгей (Ауызша сұрақ)

1. Тригонометриялық теңдеулерді шешуде не істейміз?

2. Нені білу керек?

3. Тригонометриялық теңдеулерді шешу үшін қандай

тәсілдерді қолданамыз?

Тақтада берілген теңдеулердің ішінен қайсысы мына тәсілдермен шығарылатынын көрсетіңдер:

а) Квадрат теңдеуге келтіріп шығаратын теңдеу (4, 10, 8)

ә) Біртекті теңдеулерге келтіріп шешу (1, 5, 9)

б) Дәрежені төмендету арқылы шығаратын теңдеу (2)

в) Тригонометриялық функциялардың көбейтіндісін қосындыға (айырмаға) келтіру арқылы шығарылатын есептер (6, 7)

г) Универсал (әртүрлі) тригонометриялық алмастыру арқылы шығару (11)

1) 7)

2) 8)

3) 9)

4) 10)

5) 11)

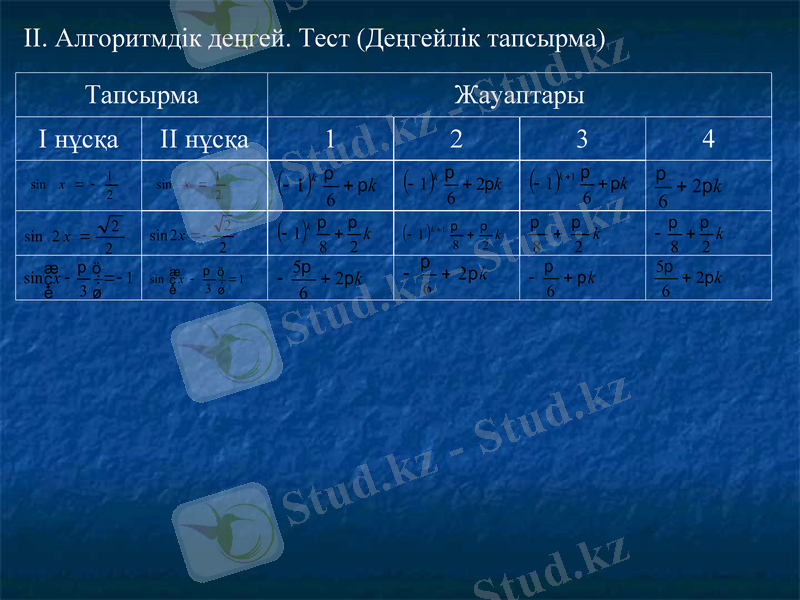
ІІ. Алгоритмдік деңгей. Тест (Деңгейлік тапсырма)

Тапсырма

Жауаптары

І нұсқа

ІІ нұсқа

ІІІ. Эвристикалық деңгей (Математикалық диктант)

І нұсқа

ІІ нұсқа

1. Анықтамасын тұжырымдаңдар

а) санның арксинусы

ә) санның арккатангисі

а) санның арккосинусы

ә) санның арктангесі

2. Теңдеулердің шешімдерінің жалпы түрінің формулаларын жазыңдар

3. Теңдеулердің шешімдерінің дербес түрлерінің формуласын жазыңдар

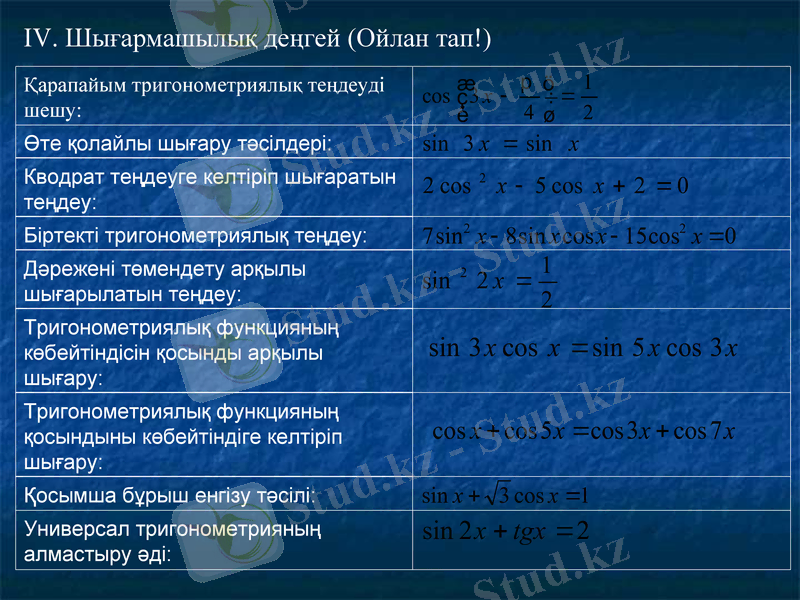
IV. Шығармашылық деңгей (Ойлан тап!)

Қарапайым тригонометриялық теңдеуді шешу:

Өте қолайлы шығару тәсілдері:

Кводрат теңдеуге келтіріп шығаратын теңдеу:

Біртекті тригонометриялық теңдеу:

Дәрежені төмендету арқылы шығарылатын теңдеу:

Тригонометриялық функцияның көбейтіндісін қосынды арқылы шығару:

Тригонометриялық функцияның қосындыны көбейтіндіге келтіріп шығару:

Қосымша бұрыш енгізу тәсілі:

Универсал тригонометрияның алмастыру әді:

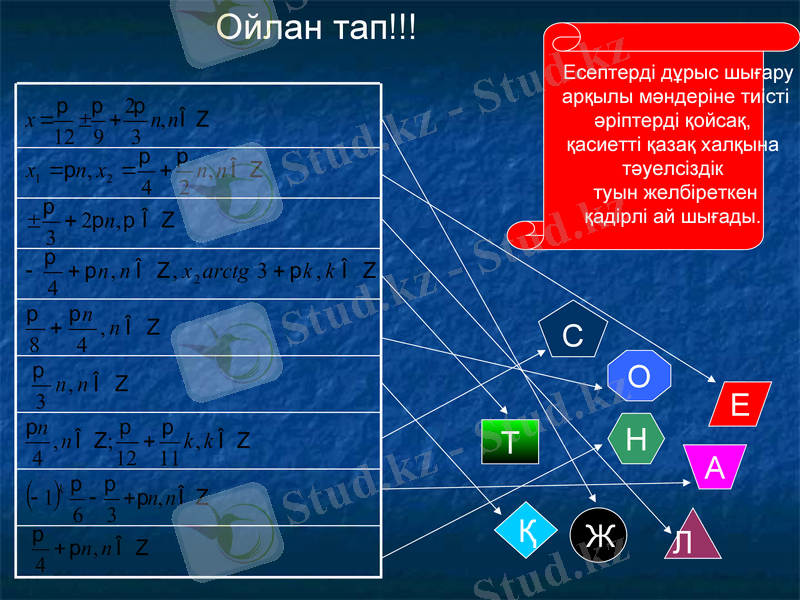
Ойлан тап!!!

Есептерді дұрыс шығару

арқылы мәндеріне тиісті

әріптерді қойсақ,

қасиетті қазақ халқына

тәуелсіздік

туын желбіреткен

қадірлі ай шығады.

Қарапайым тригонометриялық теңдеулер

шешімдерінің жалпы түрі

Шешімдердің дербес түрлері

Қорытынды

Бүгінгі сабақта біз тригонометриялық теңдеулерді шешудің әртүрлі тәсілдерін қолдану арқылы көптеген есептерді шығарып дағдылану нәтижесінде, тәжірибемен ғана келетінін көрдік.