Толымсыз квадраттық

Сабақ тақырыбы:

Квадраттық теңдеулерді формула бойынша шешу.

Алгебра. 8 сынып.

Сабақ мақсаты:

Біліктілік: Квадраттық теңдеулерді формула көмегімен шығаруды үйрету, толымсыз квадраттық теңдеулер туралы алған білімдерін бекіту.

Дамытушылық: Оқушылардың ақыл-ойын дамыту, ойлау қабілетін жетілдіру, есеп шығарудың жаңа түрлерін меңгерту және ойдан ой туындатуға, әр сөзді, айтылған ойды дәлелдеуге үйрету.

Тәрбиелік: Оқушылардың алгебра пәніне қызығушылығын арттыру, оқушыларды алғырлыққа, шапшандыққа тәрбиелеу.

Қайталау сұрақтары

Қандай теңдеуді квадраттық теңдеу деп атайды?

2. Квадраттық теңдеудегі a, b, c сандары қалай аталады?

3. Қандай теңдеуді толымсыз квадраттық теңдеу деп атайды?

4. Толымсыз квадраттық теңдеулердің неше түрі бар?

5. Толымсыз квадраттық теңдеудің әр түрінің неше түбірі бар болады?

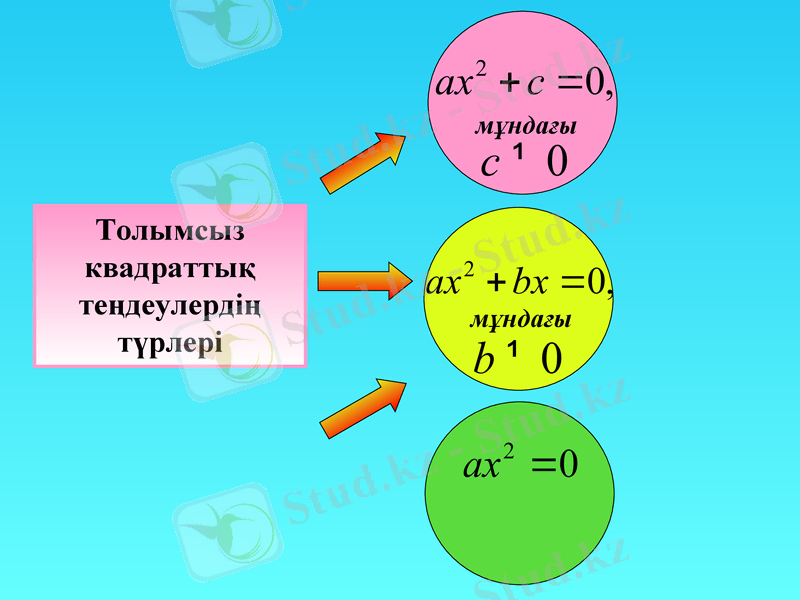
Толымсыз квадраттық теңдеулердің түрлері

Мысалы:

теңдеудің екі жағын да -ға бөліп, онымен мәндес болатын келтірілген квадраттық теңдеу шығарып аламыз

Осы теңдеуді түрлендірейік:

теңдеуі

теңдеуімен

мәндес. Мұның түбірлерінің саны

бөлшегінің

таңбасына тәуелді болады.

болғандықтан,

- оң сан болады, сондықтан бұл бөлшектің

таңбасы оның алымының, яғни өрнегінің таңбасымен

анықталады. Осы өрнекті квадраттық

теңдеуінің дискриминанты деп атайды. Мұны D әрпімен

белгілейді, яғни Енді екінші теңдеуді

мына түрде жазамыз:

-ға тәуелді мүмкін болатын әр түрлі жағдайларды қарастырайық.

Енді

1. Егер

болса, онда

Сонымен, бұл жағдайда теңдеуінің екі түбірі болады:

Қысқаша былай жазуға болады:

мұны квадраттық теңдеудің түбірлерінің формуласы деп атайды.

2. Егер болса, онда

Бұдан

Бұл жерде теңдеудің бір түбірі болады

3. Егер болса, онда бөлшегінің мәні теріс

болады, сондықтан

теңдеуінің түбірлері жоқ.

Онда теңдеудің де түбірлері жоқ болады.

Сонымен,

екі түбірі болады

бір түбір болады

түбірлері жоқ

1-мысал

2-мысал

3-мысал

Жауабы: түбірлері жоқ.

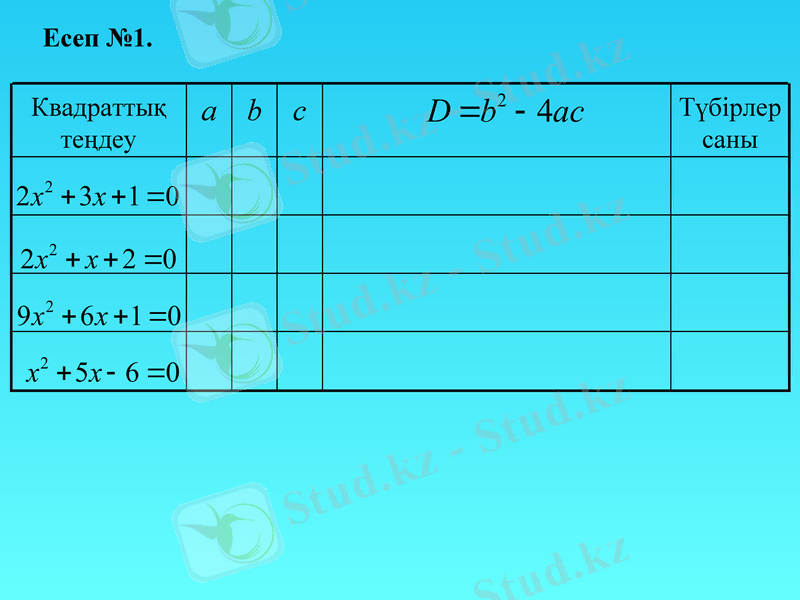
Есеп №1.

Квадраттық теңдеу

Түбірлер

саны

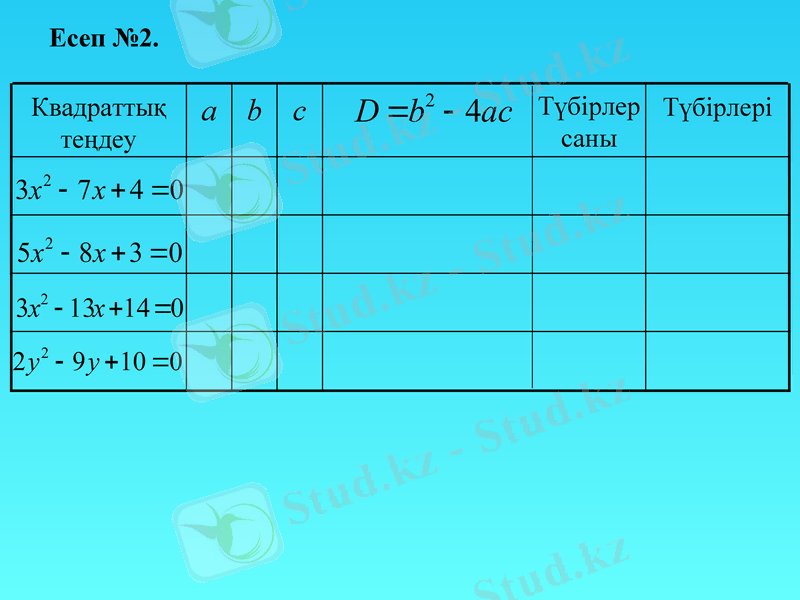
Есеп №2.

Квадраттық теңдеу

Түбірлері

Түбірлер

саны

Деңгейлік тапсырмалар

үшмүшесі 1-ге тең мән қабылдайды.

х-тің қандай мәндерінде

көпмүшелерінің мәндері тең болады.

және

Жалпы түрі:

Келтірілген квадраттық теңдеу

Теңдеудің шешімі жоқ

Егер a+b+c=0, онда х1 = 1, х2 = Егер a + c=b, онда х1 =-1, х2 =

Теңдеуді шешіңіз: х2 + 6х - 7= 0 Теңдеуді шешіңіз: 2х2 + 3х +1= 0

1 + 6 - 7 =0, онда х1=1, х2 = -7/1=-7. 2 - 3+1=0, онда х1= - 1, х2 = -1/2

Жауабы: х1=1, х2 =-7. Жауабы: х1=-1, х2 =-1/2.

Теңдеуді шешіңіз: 5х2 - 7х +2 =0 Теңдеуді шешіңіз: 5х2 - 7х -12 =0

11х2 +25х - 36=0 11х2 +25х +14=0

345х2 -137х -208=0 3х2 +5х +2=0

3х2 +5х - 8=0 5х2 + 4х - 1=0

5х2 + 4х - 9=0 х2 + 4х +3=0

Ауызша шешу жолдары

Тест тапсырмалары

1. Теңдеуді шешіңіз:

2. Теңдеуді шешіңіз:

3. Теңдеуді шешіңіз:

4. Теңдеуді шешіңіз:

5. Теңдеуді шешіңіз:

6. Теңдеуді шешіңіз:

Барлық рационал және иррационал сандардан тұратын сандар жиыны.

не болып табылады?

функциясының графигі.

түріндегі квадрат теңдеу қалай аталады?

формуласымен не табылады?

Сөзжұмбақты шешу

Үйге тапсырма:

№151, №155

Ұқсас жұмыстар

Толық квадрат Келтірілген квадрат

Квадрат теңдеудің түрлері

Квадраттық теңдеулерді формула бойынша шешу

Теңдеудің түбірін табыңдар

Шүкірлік негізгі мектебі

Квадраттық теңдеулерді формула арқылы шешу

Дискриминант және квадрат теңдеудің түбірлері

Квадрат теңдеу түбірлерінің формулалары

Толымсыз квадрат теңдеулерді шешу

Сабақтың мақсаттары

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz