Толық квадрат теңдеулерді шешу формулалары

Презентация қосу

Теңдеулер әлеміне саяхат!
8 “б” СЫНЫП.

Семей 2009-2010 оқу
жылы.
Семей қаласының Т.Ы.Аманов атындағы №16
орта мектептің математика пәні мұғалімі

Чултуков Нартай Советханұлы
Сабақтың мақсаты: оқушылардың
теңдеулерді шешу тақырыбы бойынша алған
білімдерін жүйелеу.
Сабақтың міндеті:
а) БІЛІМДІЛІК: Алған білімдерін яғни теңдеулерді
шешудің формулалары мен ережелерін өмірде,
математикалық есептеулерде, практикалық іс-
әрекеттерде қолдана білу ;
ә) ДАМЫТУШЫЛЫҚ: оқушылардың ойлау, логикалық
ойлау қабілеттерін, білік дағдыларын дамыта отырыпп,
интеллектуалдылығы мен ой ұшқырлығын
қалаптастыру;
б) ТӘРБИЕЛІК: Есеп шешімін іздеу, қиыншылықты жеңуге,
ұйымшылдыққа, дербестікке, дәлдәкке тәрбиелеу.
Теңдеулер әлемі әлі толық зерттелмеген. Сіздер теңдеулерді шешуді
ойға қонымсыз абстракциялы ұғым деп түсінбеңіздер, керісінше,
оны - кез келген оқиғаның ақиқат не жалған екендігіне көз жеткізу
деп біліңіз. Егер сіз шындыққа жаны құмар адам болсаңыз, онда
өмірдің сізге қойған сансыз сауалдарына жауап беруге тырысасыз.
Өмірдің біз білмейтін беймәлім сырлары біз білетіннен
гөрі миллион, миллиард, тіпті, триллион еседен де әлде
қайда көп. Ал сол тылсым дүниенің тұңғиығына үңілу
үшін: терең білім, темірдей төзім және түпкілікті сенім
керек.
Адамдар бір шаруаның шешімін таппағанда,
түсініксіз тығырыққа тірелгенде, бұл бір
ЖҰМБАҚ НӘРСЕ екен деп айтып жатады. Ал
математиканың жұмбағы –ТЕҢДЕУЛЕР.

МАТЕМАТИКА-дүниенің формуласы.
Г. Галилей.
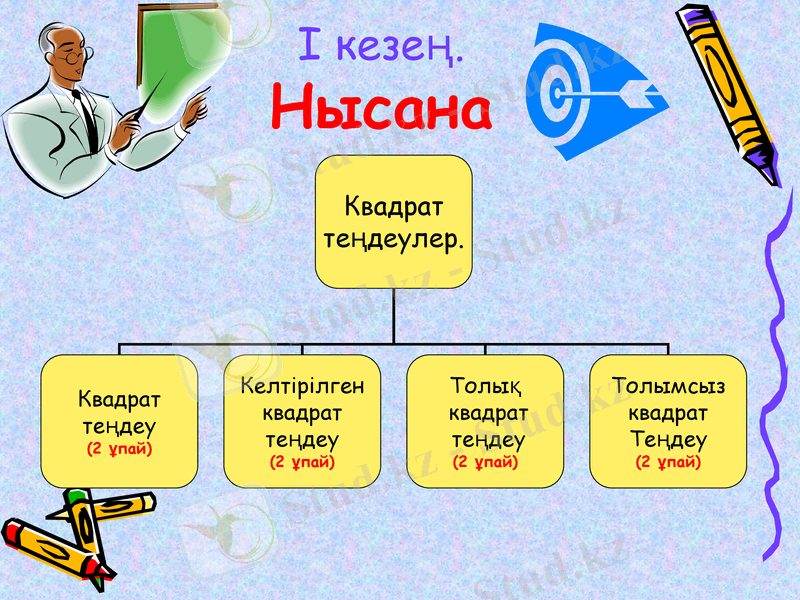
І кезең.
Нысана
Квадрат
теңдеулер.

Келтірілген Толық Толымсыз
Квадрат
квадрат квадрат квадрат
теңдеу
(2 ұпай) теңдеу теңдеу Теңдеу
(2 ұпай) (2 ұпай) (2 ұпай)
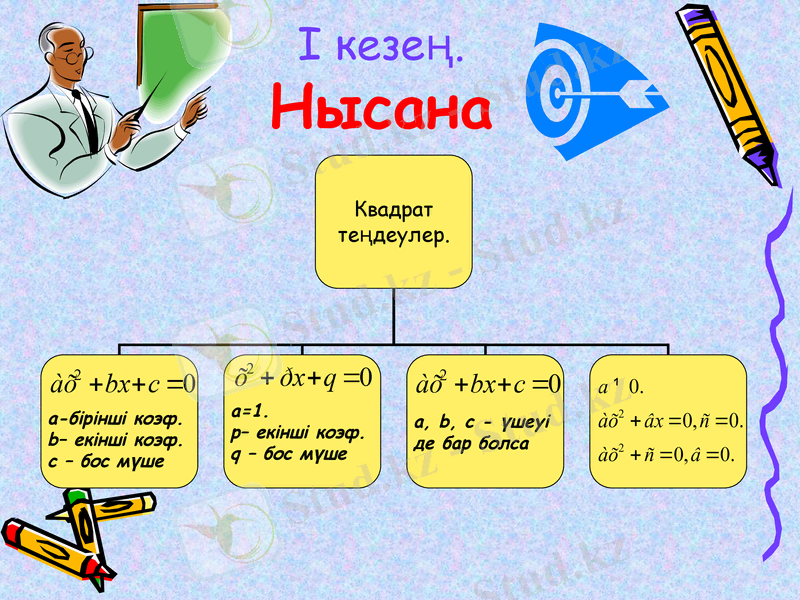
І кезең.
Нысана
Квадрат
теңдеулер.

àõ bx c 0 õ2 ðx q 0 àõ 2 bx c 0 a 0.
a=1.
а-бірінші коэф. a, b, с - үшеуі àõ2 âx 0, ñ 0.
b– екінші коэф. p– екінші коэф.
де бар болса
с – бос мүше q – бос мүше àõ2 ñ 0, â 0.
ІІ кезең.
Қорамсақ
1. Толық квадрат теңдеулерді шешу
формулалары. (әр формула 1 ұпай)
2. Дискриминант сөзінің мағынасы. (1 ұпай)
3. Толымсыз квадрат теңдеулерді шешу жолдары.
(әр түрі 1 ұпай)
4. Виет теоремасына кері теорема. (2 ұпай)
5. Рационал теңдедің анықтамасы. (1 ұпай)
6. Рационал теңдеуді шешу алгоритмі. (2 ұпай)
Егер квдрат теңдеу толық болса,
ax bx
түрінде болса, онда дискриминант c
табу 0
арқылы шешеміз:
D b 4ac
b D
1. D 0, x1 / 2
2a
b
2. D 0, x1 x 2
2a
3. D 0, (шешімі жоқ)
c
4. а+b+c=0 болса, x1 1, x2 .
a
онда
5. а+c=b болса, онда c
x1 1, x2 .
a
ІІІ кезең.
Жебе
Теңдеуді шеш: 2
x 14 õ 24
0 2 ұпай
x 4
õ 3 x 2 0 1 ұпай

3 x 5 x 2 0 1 ұпай
Теңдеуді шеш:
õ 12 x 13
0 2 ұпай
x 1
õ 2 x 24 0 1 ұпай

2 x x 3 0 1 ұпай
2
3x 4 x 20
• Теңдеуді шеш:
0 2 ұпай

x 4
9x 6 x 1 0 1 ұпай

õ 7 x 12 0 1 ұпай
2
• Теңдеуді шеш: 6x 5x 4
0 2 ұпай

5 x
4 x 12 x 9 0 1 ұпай

X 10 x 25 0 1 ұпай
• Теңдеуді шеш:
x 5 x 5
2 ұпай

x 5 x 5
X 6x 9 0 1 ұпай

9 x 24 x 16 0 1 ұпай
• Теңдеуді шеш: x 4 10 2 x
2 ұпай

2 x
2 x(5 x 7) 2 x 5 1 ұпай

2 2
( x 5) 3x x 14 1 ұпай
ІV кезең
Мерген.
Берілген түбірлер бойынша
квадрат теңдеу құрыңдар:

x1 3 , x2 5 x1 7, x 2 4 3

x1 2 3 , x 2 3 3 x1 2, x 2 5
Берілген түбірлер
бойынша квадрат теңдеу
құрыңдар:

1 5 1 5
1. және 2. 2 3 2 және
2 3 2
2 2
3 3

3. a b және a b
Жаңа жылдық сыйлық!
• Екінші коэффициенті -15, ал
түбірлерінің бірі екіншісінен екі
есе артық болатын квадрат
теңдеу құрыңыз.
x 2 15 x 50 0

Жауабы:
Жаңа жылдық сыйлық!
• Екінші коэффициенті -15, ал
түбірлерінің бірі екіншісінен екі
есе артық болатын квадрат
теңдеу құрыңыз. 3x 15
x1 x2 15 2
x1 x 2 15
x1 2 x2
x 2 5
x 1 x 2 50
x1 10

Жауабы: x 15 x 50 0
Тапқан – тапқандікі,
Көкпар -
тартқандікі.
Квадрат түбір анықтамасын қолданып,
теңдеулерді шешіңдер:

1 3 õ 2 õ 4 5 25 õ 2 4 õ 7 7
Х=-1 Х=2 Х=3 Х=4
9 2
1. ХV ғ. Самарқанд ғалымы, “Арифметика кілті” еңбегінің авторы?
2. Әріпті өрнекті енгізген ХVІ ғ фрацуздық көрнекті математик?
3. “Хисаб ал-джебр вал-мукабала” еңбегінің авторы, ІХ ғ. Орта
Азияның белгілі математигі?
4. Мектебіміздегі №15-і кабинет кімнің атымен аталған?
Қорытындылау:
• Кез келген квадрат теңдеуді шешуге
болады. Ол үшін:
1) жалпы жағдайда ДИСКРМИНАНТТЫ табу
формуласын біліуіміз қажет, оның үш
жағдайын. D>0. D=0. D<0;
2) Келтірілген квадрат теңдеу болғанда, оны Виет
теремасы арқылы шешу;
3) Дербес жағдайларды мұқият ескеру:
ñ
õ1 1, õ2
a+b+c=0 болғанда,
à
ñ
õ1 1, õ2
a+c=b болғанда,
à
4) Рационал теңдеулерді шешкенде ең бірінші
ММЖ-ны анықтап алу, БӨГДЕ түбірден сақ болу.

Үйге тапсырма: №182-184
есептер.
Таразылау.
ҰПАЙЛАРЫ
І ІІ ІІІ кезең ІV кезең ЖИЫНЫ
кезең кезең
1 ТОП

2 ТОП

3 ТОП

4 ТОП
Шығамын десең биік шыңның басына,
Адал досың – Біліміңді ал қасыңа.
Зула, топ жар! Бәйгеге түс, бекем
бол,
Тула, толқы, тебірен бірақ тасыма!

Назарларыңызға рахмет!

Ұқсас жұмыстар

Квадрат теңдеулерді шешу тәсілдері

Оқушы білімін тексеру

Мектеп математикасындағы квадраттық теңдеулерді шешу жолдары

Квадрат теңдеу түбірлерінің формулалары

Квадрат теңдеулерді шешудің әр түрлі тәсілдері

Квадрат теңдеулерді шешу

Квадрат теңдеудің түрлері

Жұп коэффициенті бар теңдеуді шешу

Анықталмаған интеграл

Квадрат теңдеулерге қайталап есеп шығару.Виет теоремасы

Пәндер