Презентациялар

Теңдеудің түбірін табыңдар

Квадрат теңдеу тарауын

қайталау.

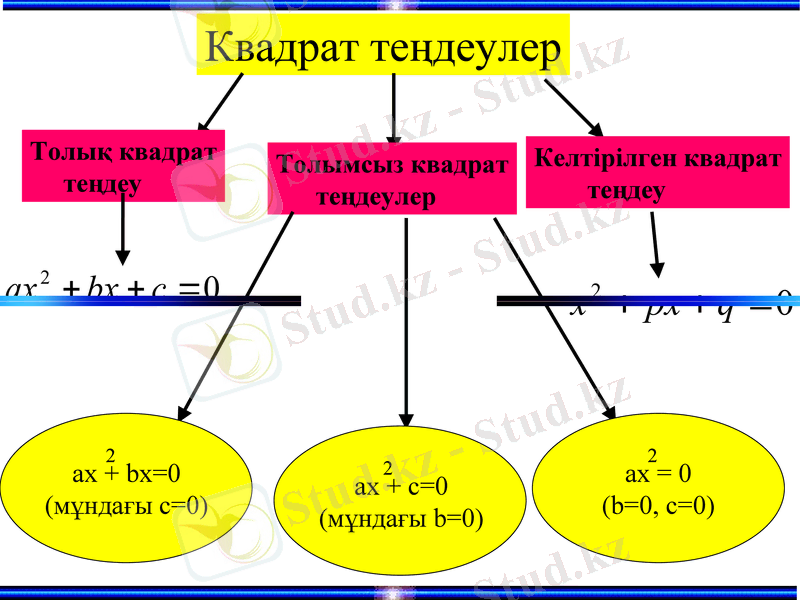
Квадрат теңдеулер

Толық квадрат

теңдеу

Толымсыз квадрат

теңдеулер

ax + bx=0

(мұндағы с=0)

ax + c=0

(мұндағы b=0)

ax = 0

(b=0, c=0)

Келтірілген квадрат

теңдеу

2

2

2

(b=0, c=0)

СҰРАҚ-ЖАУАП

aх2-bх+c=0 түріндегі теңдеу квадрат теңдеу деп аталады, мұндағы х - айнымалы, а, b және с - кез келген сандар және a≠0; а, в және с - сандары квадрат теңдеудің коэффициенттері

b немесе с, немесе b мен с нөлге тең

болатын дербес жағдайдағы квадраттық

теңдеу толымсыз квадрат теңдеу деп

аталады.

Егер толық квадрат теңдеудегі бірінші коэффициент 1 - ге тең (a=1) болса,

онда келтірілген квадрат теңдеу деп аталады.

Квадрат теңдеуді дұрыс теңдікке

айналдыратын айнымалының мәні

теңдеудің түбірі деп аталады.

Квадрат теңдеуді шешу дегеніміз - оның барлық түбірлерін табу немесе түбірлері жоқ екенін көрсету.

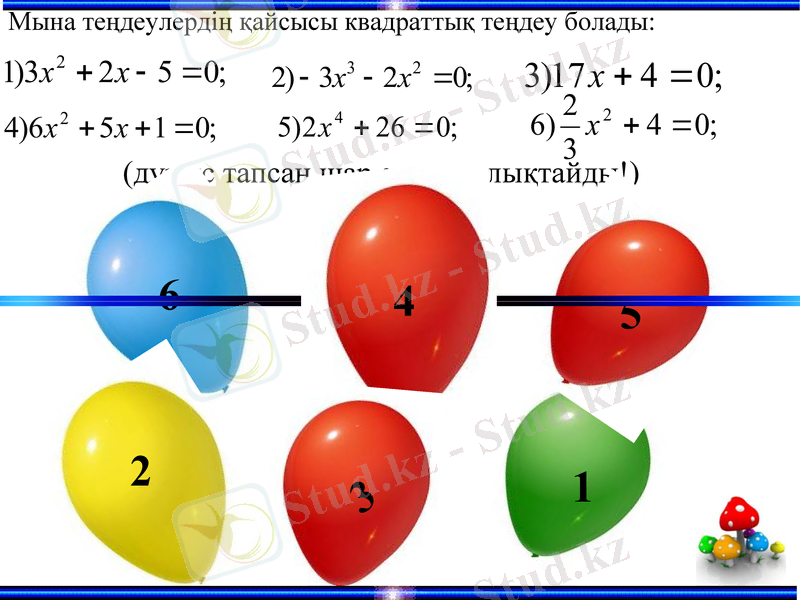
(дұрыс тапсаң шар әуеге қалықтайды!)

Мына теңдеулердің қайсысы квадраттық теңдеу болады:

Жалқаудың екі досы бар, бірі-ұйқы, бірі күлкі.

Отыз тістен шыққан сөз, отыз рулы елге тарайды.

Жеті жұрттың тілін біл, жеті түрлі білім біл.

Мақалдардың жалғасын тауып, астында берілген тапсырманы орында

толық

толық

толымсыз

толымсыз

толымсыз

келтірілген

келтірілген

келтірілген

Қандай квадрат теңдеу екенін ата

(дұрыс тапсаң құс әуеге қалықтайды!)

түрінде берілген

теңдеулер толық

квадрат теңдеулер

деп аталады.

болса,

онда ол келтірілген

Квадрат теңдеу деп

аталады.

түрінде

берілген теңдеу толымсыз

квадрат теңдеу деп аталады.

Қатесін тап

Толымсыз квадрат теңдеулер

1-ге тең болса келтірілген квадрат теңдеу деп аталады.

Толық квадрат теңдеу деп аталады.

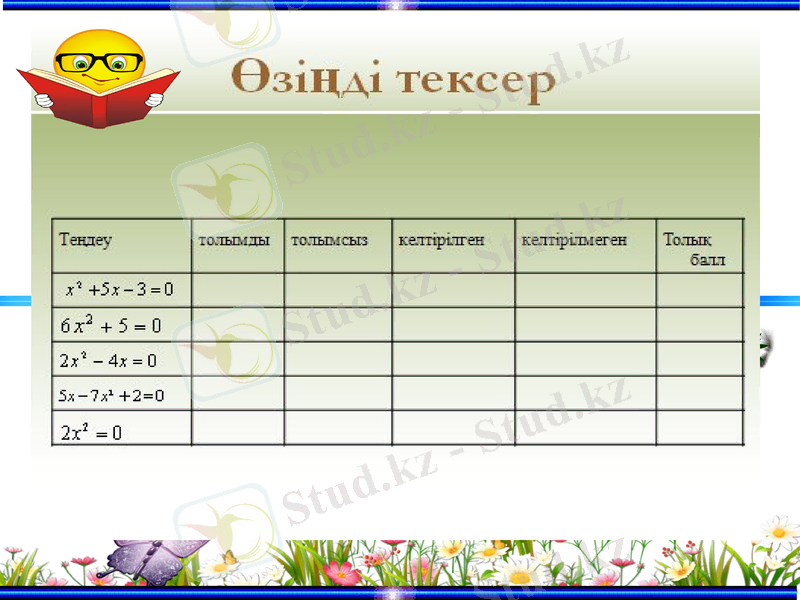
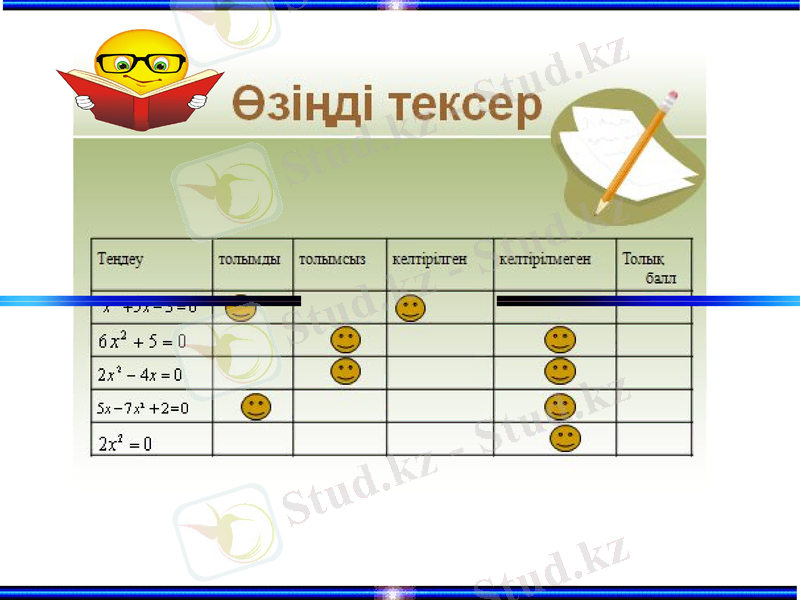
(дұрыс тапсаң құс әуеге қалықтайды!)

1-деңгей

Теңдеуді шешіңдер:

Теңдеудің түбірлерін табыңдар:

Квадраттық теңдеуді екімүшенің квадратын бөліп алу

Тәсілімен шешіңдер:

2-деңгей

Теңдеуді шешіңдер:

Теңдеудің түбірін табыңдар:

Теңдеудің түбірлерін табыңдар:

3-деңгей

Теңдеуді шешіңдер:

Теңдеудің түбірлерін табыңдар:

Теңдеуді шешіңдер:

Оқулықпен жұмыс:

№344 (1-3), 345 (1-3)

Үйге тапсырма:

№344 (2-4), 345 (2-4)

Ұқсас жұмыстар

“Бір айнымалысы бар сызықтың теңдеу”

Қызықты есептер

Теңдеудің түбірлерін табыңдар

Квадрат теңдеу түбірлерінің формулалары

Виет теоремасы туралы ақпарат

Келтірілген квадраттық теңдеуді көрсет

Виет теоремасы

Виет теоремасын үйрену

Квадарат теңдеу тарауын қорытындылау

Квадрат теңдеулерді шешу

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz