Квадрат үшмүшені көбейткіштерге жіктеуңдер

Квадрат үшмүшені көбейткіштерге жіктеу.

Пән мұғалімі: Булекбаева А.

2014-2015 оқу жылы

Ашық сабақ

Сабақтың мақсаты:

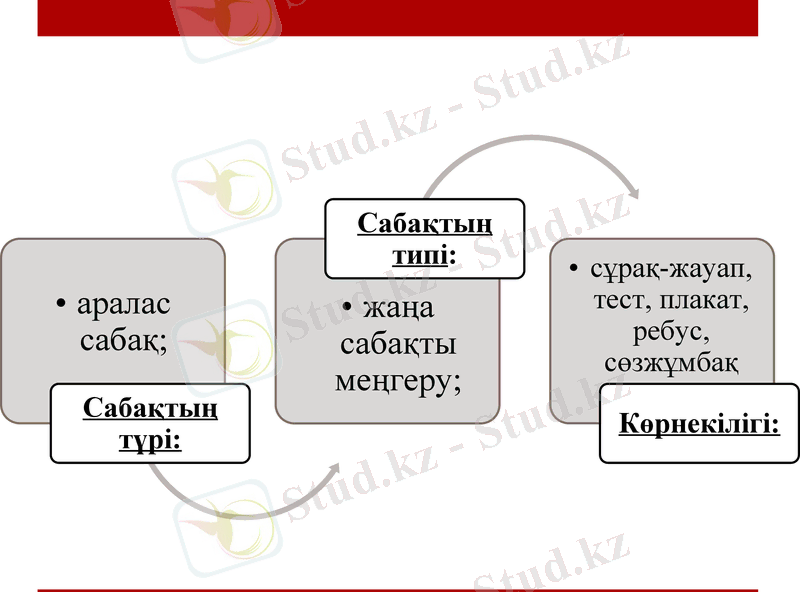
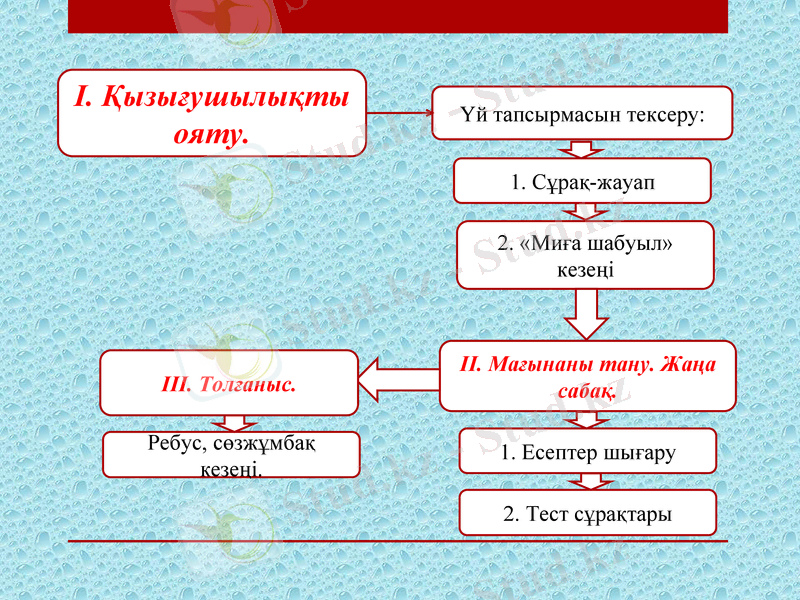
ІІ. Мағынаны тану. Жаңа сабақ.

І. Қызығушылықты ояту.

1. Сұрақ-жауап

2. «Миға шабуыл» кезеңі

Үй тапсырмасын тексеру:

ІІІ. Толғаныс.

1. Есептер шығару

2. Тест сұрақтары

Ребус, сөзжұмбақ кезеңі.

1. Сұрақ-жауап:

Төртінші дәрежелі теңдеуді шешу үшін не қолданамыз?

Квадрат теңдеу дегеніміз не?

Толымсыз квадрат теңдеу дегеніміз не?Жазылуы қандай?

Квадрат теңдеудің түрлерін ата?

Толымсыз квадрат теңдеу дегеніміз не?

Квадрат үшмүше дегеніміз не?

Квадрат теңдеу түрлері

2. «Миға шабуыл» кезеңі:

ІІ. Мағынаны тану. Жаңа сабақ

Алдымен х2+px+q келтірілген квадрат үшмүшесін көбейткіштерге жіктейік. Бұдан былай х2+px+q=0 квадрат теңдеуінің түбірлерін х2+px+q квадрат үшмүшесінің түбірлері деп атаймыз. Бұл квадрат үшмүшенің түбірлері х2+px+q=0 теңдеуінің түбірлерімен бірдей болғандықтан, -(х1+x2) =p, х1∙x2=q теңдіктері орындалады. Сонда

х2+px+q=х2-(х1+x2) х+х1∙x2=х2-х1х+х1x2=х(х-х1) -х2(х-х1) =(х-х1) (х-х2) теңдігін аламыз. Сонымен, егер х1 және х2 сандары х2+px+q квадрат үшмүшесінің түбірлері болса, онда х2+px+q=(х-х1) (х-х2) теңдігі орындалады.

Ал жалпы жағдайда, aх2+bx+c квадрат үшмүшесінің түбірлері aх2+bx+c=0 теңдеуінің немесе теңдеуінің түбірлерімен бірдей болады. Егер оның түбірлері х1, x2 болса, онда жоғарыдағы көрсетілгендей теңдігі орындалады. Сондықтан

Сонымен, егер х1 және x2 сандары aх2+bx+c квадрат үшмүшесінің түбірлері болса, онда

aх2+bx+c=а(х-х1) (х-х2) теңдігі орындалады.

1-мысал. х2-6x+8 квадрат үшмүшесін көбейткіштерге жіктейік. Оның түбірлері: х1=2, х2=4 болғандықтан, х26x+8=(х-2) (х-4) теңдігін аламыз.

2-мысал. 2х2-x-6 квадрат үшмүшесін көбейткіштерге жіктейік. Оның түбірлері: х1=-1, 5; х2=2 болғандықтан, 2х2-x-6=2(х-(-1, 5) ) (х-2) =2(х+1, 5)

(х-2) =(2х+3) (х-2) теңдігі орындалады.

1. Есептер шығару.

Деңгейлік тапсырмалар:

А тобы:

№326. Квадрат үшмүшені көбейткіштерге жіктеңдер:

1) х2-2x-48; 2) х2+9x-22;

В тобы:

№330. Квадрат үшмүшені көбейткіштерге жіктеуңдер:

1) ах2-(а+с) x+с; 2) 6х2+5mx+m2;

C тобы:

№341. Түбірлері бойынша теңдеулер құрастырып, оларды көпмүше түрінде жазыңдар. 1) -3; 8;

1. ах4+bx2+c=0, мұндағы а≠0 түрінде берілген теңдеу қандай теңдеу?

Биквадрат теңдеу

Квадрат теңдеу

Келтірілген квадрат теңдеу

келесі

2. Тест сұрақтары:

2. Квадрат теңдеудің неше түрі бар?

Төрт

Үш

Екі

келесі

3. 4х2-3x=0 қандай теңдеу?

Толымды квадрат теңдеу

Дұрыс жауап жоқ

Толымсыз квадрат теңдеу

келесі

4. Квадрат теңдеудің қанша түбірі болатынын қалай анықтауға болады?

Есептің берілуіне байланысты

Дискриминантқа

Өзгермейді

келесі

5. х2-8x+15=0 теңдеуінің түбірлерін Виет теоремасы арқылы жауабын жылдам тап?

2; 6

3; 5

3; 6

келесі

6. Егер 11 және -2 сандары кез-келген квадрат теңдеудің түбірлері болса, онда квадрат теңдеуді құрыңдар.

х2-10x+25=0

х2-9x-22=0

9х2-24x+16=0

келесі

7. ах2=0 (мұндағы b=0, с=0) . Бұл қандай теңдеудің жазылу түрі?

келесі

8. 2, 1х2+102, 3x+0, 8=0. Бұл қандай теңдеу, дұрысын анықта?

келесі

ІІІ. Толғаныс.

1. Ребус шешу кезеңі. Жауабы: КВАДРАТ

2. Сөзжұмбақ шешу кезеңі.

1. Квадрат теңдеудің неше түрі бар?

2. ах2+bx+c=0 түріндегі квадрат теңдеудегі а-қандай коэффициент деп аталады?

3. b мен c нөлге тең болатын дербес жағдайлардағы квадрат теңдеу қалай аталады?

4. Егер рационал теңдеудің екі жақ бөлігінде де бүтін өрнектер жазылса, онда оны қандай теңдеу деп атаймыз?

5. ах2+bx+c=0 түріндегі квадрат теңдеудегі b-қандай коэффициент деп аталады?

6. Келтірілген квадрат теңдеудің түбірлерінің қосындысы қарама-қарсы таңбамен алынған екінші коэффициентке, ал көбейтінділері бос мүшеге тең. Бұл қай теорема?