Квадрат теңдеулердің түбірлері мен дискриминант формуласы: сабақ жоспары және тапсырмалар



Қош
келдіңіздер!

« Ақтау қаласы №3 орта мектебі» мемлекеттік мекемесі .
Математика пәнінің мұғалімі
Кайрханова Айгүл
Сейсенайқызы

Сабағымыздың эпиграфы

Математика дәлдікке,
тәртіпке үйретеді
Логикалық ойды, ақылды кеңейтеді.

Оқушы білімін тексеру.
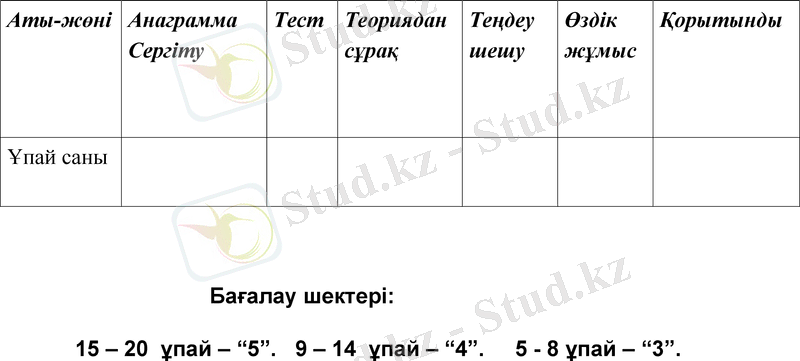
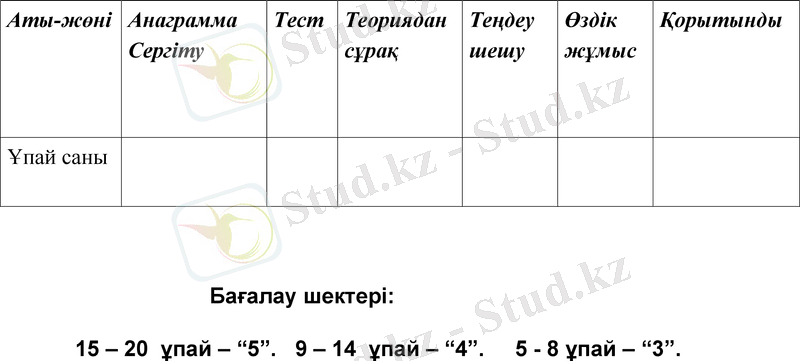
Аты-жөні
Анаграмма
Сергіту
Тест
Теориядан сұрақ
Теңдеу шешу
Өздік жұмыс
Қорытынды
Ұпай саны
Бағалау шектері:
15 - 20 ұпай - “5”. 9 - 14 ұпай - “4”. 5 - 8 ұпай - “3”.

Сергіту сәті

Анаграмма
Мына сөздерден математикалық термин құрастыр:
Ңеетду
Фэкоцинетиф
Үртіб

СҰРАҚ-ЖАУАП

aх2-bх+c=0 түріндегі теңдеу квадрат теңдеу деп аталады, мұндағы х - айнымалы, а, b және с - кез келген сандар және a≠0; а, в және с - сандары квадрат теңдеудің коэффициенттері

b немесе с, немесе b мен с нөлге тең
болатын дербес жағдайдағы квадраттық
теңдеу толымсыз квадрат теңдеу деп
аталады.

Егер толық квадрат теңдеудегі бірінші коэффициент 1 - ге тең (a=1) болса,
онда келтірілген квадрат теңдеу деп аталады.

Квадрат теңдеуді дұрыс теңдікке
айналдыратын айнымалының мәні
теңдеудің түбірі деп аталады.

Квадрат теңдеуді шешу дегеніміз - оның барлық түбірлерін табу немесе түбірлері жоқ екенін көрсету.

Шағын тест

28. 10. 2011
Сабақтың тақырыбы:
Квадрат теңдеу түбірлерінің формуласы

Білімділік:
Квадрат теңдеулерді шешуде формулаларды тиімді пайдалану дағдыларын қалыптастыру, дискриминант арқылы квадрат теңдеулерді шешу
Дамытушылық:
Алған білімдерін әр түрлі жағдайларда қолдана білуге дағдыландыру. Белсендігін көтеруге, ойлау қабілетін арттыруға, өз ойын жүйелеуге, тез шешім қабылдауға ұқсастықты, қарама-қайшылықты байқауғадағдыландыру
Тәрбиелік:
Оқушылардың білімге деген қызығушылығын арттыру. Ұжым намысын қорғай білетін, шығармашылық қабілеті дамыған тұлға тәрбиелеу. Алған білімдеріне жауапкершілікпен қарауға, өз мүмкіндігіне сенуге, үлкен жетістікке ұмтылуға үйрету
Сабақтың мақсаты.

ax2 + bx + c =0

Квадраттық теңдеудің түбірлері және дискриминант

Қосымша формулалар
Егер а-b+c=0
онда
Егер а+b+c=0
онда

Теңдеуді шешіңіздер:
2х2+3х-5=0
25х2-10х+1=0
9х2-3х+2=0
5х2-2х-7=0
а-в+с=0 5-(-2) +(-7) =0


А деңгей №128 Квадрат теңдеудің дискриминантын есептеу, қанша түбірі болатынын көрсетіңдер.
х2 - 5х - 8 = 0
3) х2 - 14х + 49 = 0

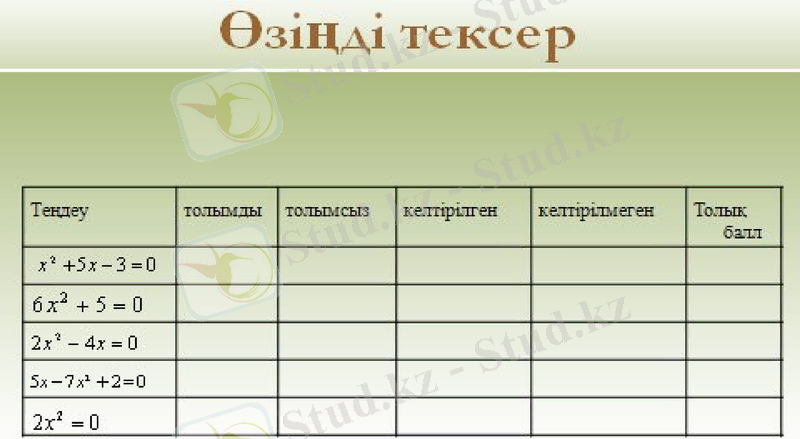
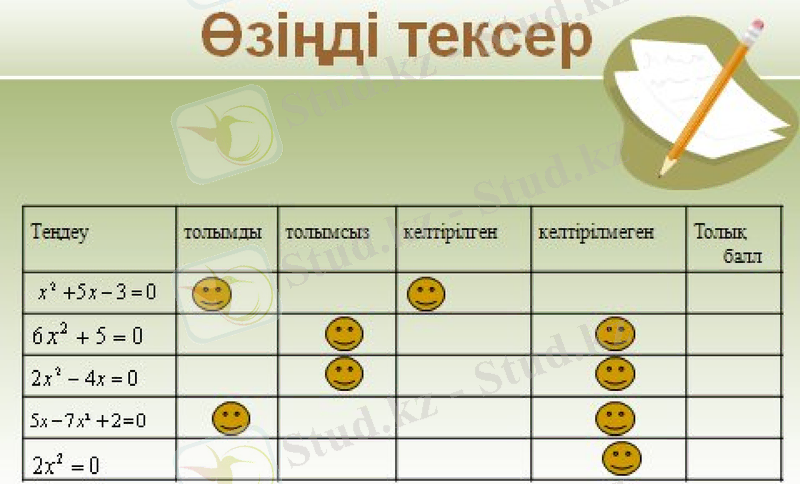
Егер квадрат теңдеу толық болса, түрінде болса, онда дискриминант табу арқылы шешеміз:
(шешімі жоқ)
а+b+c=0 болса, онда
4.
5.
а-c+b=0 болса, онда

В деңгей №134 Теңдеуді шешіңдер.
1) 2х(5х-7) = 2x2 - 5
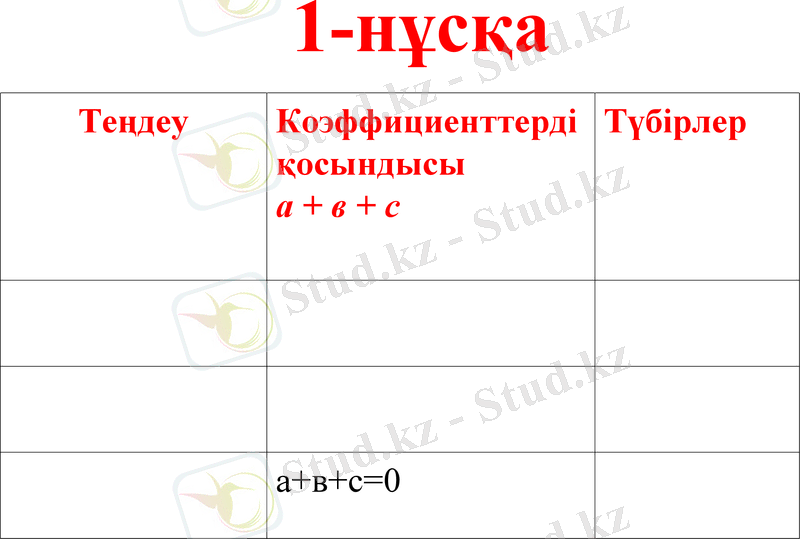
1-нұсқа
Теңдеу
Коэффициенттерді
қосындысы
а + в + с
Түбірлер
а+в+с=0
Теңдеу
а - в + с
Түбірлері
а-в+с=0
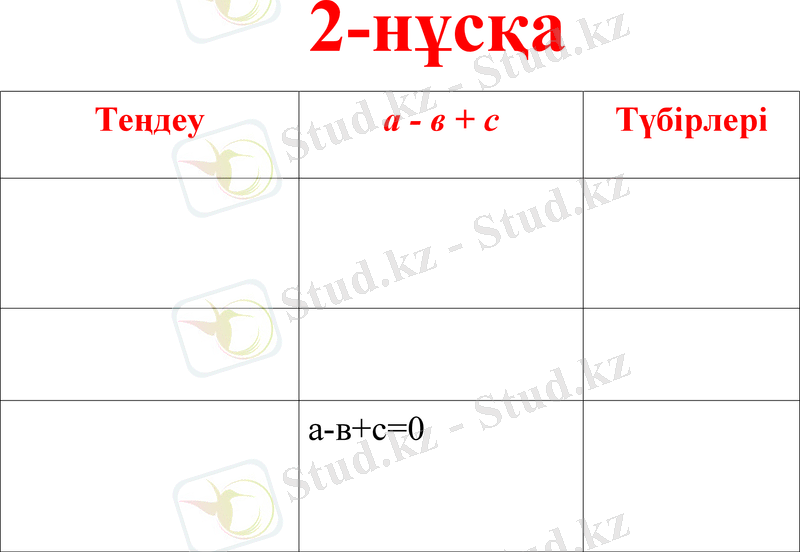
2-нұсқа

1-нұсқа
Теңдеу
Коэффициенттердің
қосындысы
а + в + с
Түбірлер
2 - 5 + 3 = 0
5 - 8 + 3 = 0
а + в + с = 0

Теңдеу
а - в + с
Түбірлері
1 - (- 2) +(- 3) = 0
1 - 3 + 2 = 0
а - в + с = 0
2-нұсқа
Аты-жөні
Анаграмма
Сергіту
Тест
Теориядан сұрақ
Теңдеу шешу
Өздік жұмыс
Қорытынды
Ұпай саны
Бағалау шектері:
15 - 20 ұпай - “5”. 9 - 14 ұпай - “4”. 5 - 8 ұпай - “3”.

VІ. Үй тапсырмасы:
“Квадрат теңдеуді шешу формулалары” тақырыбын оқу
2.
V. Оқушылар білімін бағалау

Кез келген квадрат теңдеуді шешуге болады.
Ол үшін:
Жалпы жағдайда ДИСКРМИНАНТТЫ табу формуласын біліуіміз қажет, оның үш жағдайын.
D>0. D=0. D<0;
2) Келтірілген квадрат теңдеу болғанда, оны Виет теремасы арқылы шешу;
3) Дербес жағдайларды мұқият ескеру:
a+b+c=0 болғанда,
a-c+b=0 болғанда,
Үйге тапсырма: №130 -№135 есептер.
Қорытындылау:

Жүректен-жүрекке жылы лебіз білдіру

- Мен білдім…
- Қызықтандым…
- Қиын болды …
- Мен түсіндім…
- Мен үйрендім…
- Мен шығара алдым…
- Мен өзім шығарып көрдім…

Шығамын десең биік шыңның басына,
Адал досың - Біліміңді ал қасыңа.
Зула, топ жар! Бәйгеге түс, бекем бол,
Тула, толқы, тебірен бірақ тасыма!

Тыңдағандарыңызға рахмет.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz