Герон формуласының дәлелдеу әдістері және қолданылуы

Қазақстан Республикасы Білім және ғылым министрлігі. №64 Ж. Аймауытов атындағы мектеп- гимназия

Ғылыми жұмыс

Тақырыбы: Герон формуласын дәлелдеу тәсілдері.

Дайындаған: 9 “А” сынып оқушысы

Даулетбай Бекарыс.

Пән мұғалімі: Ыдырысбаева Гүлнар

Жоспар: I. Кіріспе II. Негізгі бөлім а) Герон формуласын тригонометрия тәсілімен дәлелдеу ә) Герон формуласын Пифагор теоремасы арқылы дәлелдеу б) Герон формуласынан нені шығаруға болады? III. Қорытынды

Герон-

б. з. I ғасырында Александрияда өмір сүрген ежелгі грек инженері әрі ғалымы

Герон формуласы

Тригонометрия тәсілімен дәлелдеу

Теорема дәлелденді.

Катеттері 6 және 8 болатын тікбұрышты үшбұрыш ауданын тап.

Герон формуласы

Пифагор теоремасы

Пифагор теоремасы арқылы дәлелдеу

Теорема дәлелденді.

a=13, b=14, c=15 болса, онда үшбұрыштың ауданы қанша болғаны?

Герон формуласынан нені шығаруға болады

Тік бұрышты үшбұрыш үшін

Тең бүйірлі үшбұрыш үшін:

Тең қабырғалы үшбұрыш үшін:

Косинус теоремасы бойынша:

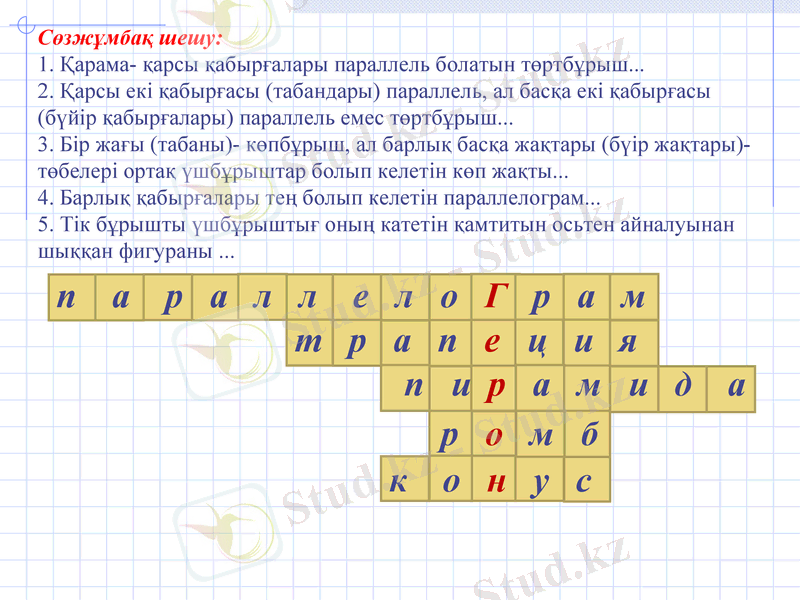
п а р а л л е л о Г р а м

т р а п е ц и я

п и р а м и д а

р о м б

к о н у с

Сөзжұмбақ шешу:

1. Қарама- қарсы қабырғалары параллель болатын төртбұрыш . . .

2. Қарсы екі қабырғасы (табандары) параллель, ал басқа екі қабырғасы (бүйір қабырғалары) параллель емес төртбұрыш . . .

3. Бір жағы (табаны) - көпбұрыш, ал барлық басқа жақтары (бүір жақтары) - төбелері ортақ үшбұрыштар болып келетін көп жақты . . .

4. Барлық қабырғалары тең болып келетін параллелограм . . .

5. Тік бұрышты үшбұрыштығ оның катетін қамтитын осьтен айналуынан шыққан фигураны . . .

Үшбұрыш ауданын үш қабырғасы бойынша есептеу формуласын Архимед (III ғ. б з. б. ) ашқан. Бірақ оның бұл еңбегі бізге жеткен жоқ. Бұл формула Герон Александрийскийдің «Метрикасында» болған (I ғ. б. з. ) және соның атымен аталып кеткен. Герон қабырғалары бүтін сан, сонымен қатар аудандары да бүтін үшбұрыштарды зерттеген. Бұндай үшбұрыштар герон үшбұрыштары деп аталады. Герондық ең қарапайым үшбұрыш - мысырлық үшбұрыш.

Қорытынды