10-сынып: Алгебра және анализ бастамалары - туынды мен дифференциалдау ережелері

Туындыны табу ережелері

Сабақтың басталу уақыты:

13. 01. 2010 жылы

сағат 11:00-де

Жезқазған қаласы

Алгебра және анализ бастамалары

10-сынып

Мырзахметова

Дариға

Өмірбайқызы

Жоғары санатты

математика пәнінің мұғалімі

Сабақтың мақсаты:

Дифференциалдау ережелерін меңгеру, туындыны есептеу ережелерін дәлелдеп, оларды практикада қолдана білу.

Қайталау сұрақтары

1. Аргументтің өсімшесі және функцияның өсімшесінің анықтамасы.

2. Туындының анықтамасы.

3. Функцияны дифференциалдау.

4. Туындыны табу алгоритмі.

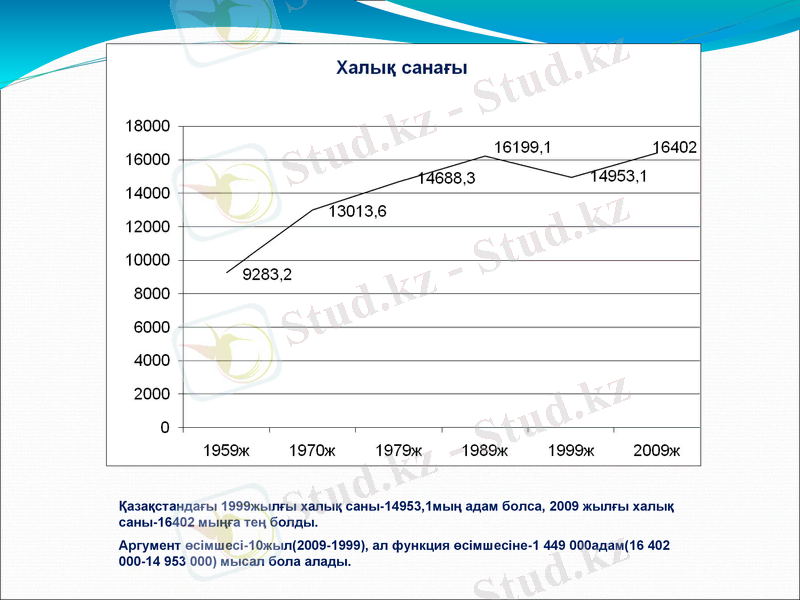
Қазақстандағы 1999жылғы халық саны-14953, 1мың адам болса, 2009 жылғы халық саны-16402 мыңға тең болды.

Аргумент өсімшесі-10жыл(2009-1999), ал функция өсімшесіне-1 449 000адам(16 402 000-14 953 000) мысал бола алады.

Қайталау сұрақтары

1. Аргументтің өсімшесі және функцияның өсімшесінің анықтамасы.

2. Туындының анықтамасы.

3. Функцияны дифференциалдау.

4. Туындыны табу алгоритмі.

Туындының анықтамасы

Функцияны дифференциалдау

lim

v0 жылдамдықпен жоғары қарай лақтырылған дененің лездік жылдамдығын(туындыны табу алгоритмі бойынша ) табу.

h (t) =v0t - gt2/2 бойынша табамыз.

h ∆t →0 болғанда -g ∆t /2→0

vлез(∆t) =v0-gt0

h‘(t) = vорт(t) = vлез(t)

Туындыны табу алгоритмі

1. Аргументке өсімшесін беру

өсімшеге сәйкес функция өсімшесін,

анықтау

3. Функция өсімшесінің аргумент өсімшесіне

қатынасын табу, яғни

4. Соңғы теңдіктен аргумент өсімшесі нөлге ұмтылғандағы шекті анықтау:

lim

∆ X

∆ y=f(x+∆ X) -f(x)

∆ X→0

Шегін табу

∆ X-ке бөлеміз

Туындыны табу алгоритмі

Функция

y=x3

y=x2

y=x

y=x8

Дәрежелі функцияның туындысын есептеу формуласы

1-ден үлкен кез келген N үшін y=xn дәрежелі функция туындысы

(xn) '=nxn-1

формуласымен есептелінеді

Туынды табу алгоритмі

(u+υ) '

∆ X

∆ y=f(x+∆ X) -f(x)

∆ X→0

Шегін табу

(u- υ) '

(u+υ-g) '

∆ X-ке бөлеміз

Қосындының туындысы (u+v) ’=u’+v’

u'+ υ '-g'

u '- υ'

u' + υ'

Туынды табу алгоритмі

(u· υ) '

Көбейтіндінің туындысы (u·v) ’=u’·v+u·v’

∆ y=f(x+∆ X) -f(x)

∆ X→0

Шегін табу

∆ X-ке бөлеміз

∆ X

u'υ +u υ'

Cu'

(Cu) '

с-тұрақты сан, С'=0

Туындыны табу ережелері тек берілген нүктеде немесе

берілген аралықта дифференциалданатын функцияға

қолданылады.

Жаңа сабақты бекіту (кітаппен жұмыс)

№175

a) f(x) =x2-3X+1; б) 7x8 -8X7

№176

а) f(x) =2x2+3X; б) x6 -X3 +1

№177

a) f(x) =3x2+8X+2 б) 3/2 x2+4X-1

А тобының есептері

№180

а)

ә) f(x) =

№181

f(x) функциясының берілген нүктедегі туындысының мәнін есептеңдер:

а) f(x) =3x-4x3, X=5;

б) f(x) =(1+2x) (2x-1), x=0. 5

№186

f(x) =(x2+5) (x2-4)

f(x) =x4-4, 5x2+2

№187

Үйге тапсырма:

Бөліндінің туындысын дәлелдеу.

(uvg) ' салдарын дәлелдеу.

№ 175-179 (ә, в), №181 (а, ә) .

Жеке оқушыға №186, 187 (б, в) .

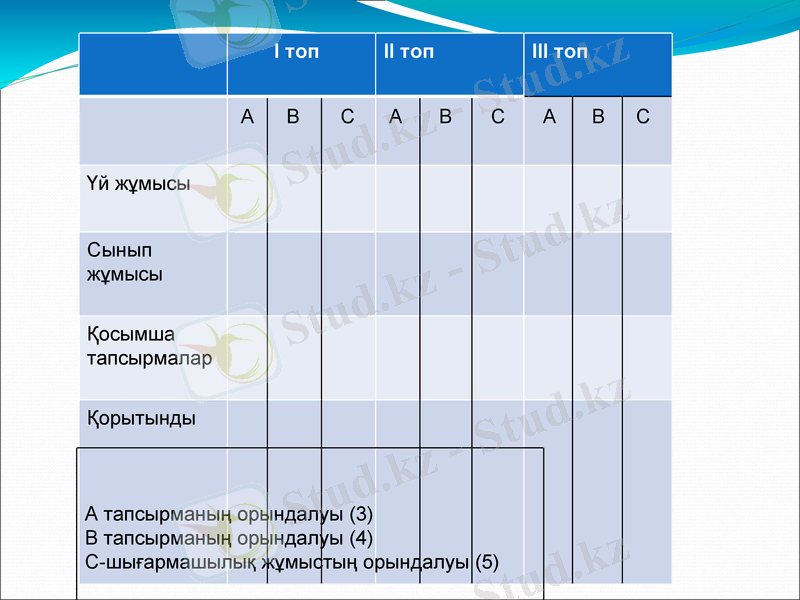
I топ

II топ

III топ

Үй жұмысы

Сынып жұмысы

Қосымша тапсырмалар

Қорытынды

А тапсырманың орындалуы (3)

В тапсырманың орындалуы (4)

С-шығармашылық жұмыстың орындалуы (5)

Ұқсас жұмыстар

Бір айнымалы функцияның дифференциалдық есептеулері: туынды, дифференциалдау ережелері, айқындалмаған функциялардың туындылары және жоғары реттік туындылар

Туынды табу ережелері мен күрделі және дербес туындыларды есептеу

Бірыңғай ұлттық тестке интерактивті дайындық ойыны: алгебра, тригонометрия, туынды, логарифмдер және геометрия

11-сынып алгебра: логарифмдік теңдеулерді қайталау және шешу әдістері

11-сынып алгебра: логарифмдік теңдеулерді шешу

9-сынып алгебра: Геометриялық прогрессия - сабақ жоспары мен тапсырмалары

10-сыныпқа арналған интерактивті бекіту сабағы мен тест: Туындыны есептеу ережелері

Функцияның туындысы (дифференциалдау): ережелер, есептер және сабақ жоспары

Объектіге бағытталған бағдарламалау: туынды кластар, кіру ережелері және полиморфизм

Ізденіс - шығармашылық бастауы: 7-10 сынып оқушыларына арналған интеллектуалдық сайыс және өткізу ережелері

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz