Квадраттық функциялар: дербес түрлері мен графиктерін салу

Квадраттық функция.

Квадраттық функцияның y= ax2+n

y= a(x-m) 2 дербес түрлерін қайталау

және белгілі графиктердің көмегімен

квадраттық фунцияның графиктерін

салудағы оқушылардың білімдерін бекіту

Сабақтың мақсаты:

Теориялық материалды қайталау

1. Қандай фукцияны

квадраттық функция

деп атайды?

у = ах2+bх+с түріндегі функцияны

квадраттық функция деп атайды

Мұндағы а, b, c - нақты сандар, а≠0,

х - тәуелсіз айнымалы.

у=5х2-6 4) у=4х2

2) у=7х-1 5) у=x3+x+1

3) у=-3х2+х+7 6) у=-9х2+4х

2. Берілген функциялардың қайсысы

квадраттық функция болады?

3. y=ax2

y= ax2+n

y= a(x-m) 2

функциялардағы а коэффициенті нені білдіреді?

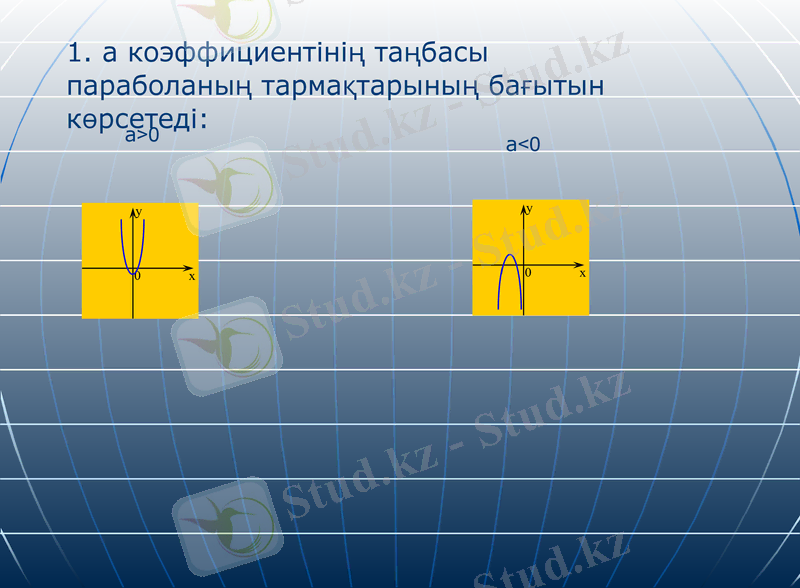
1. а коэффициентінің таңбасы параболаның тармақтарының бағытын көрсетеді:

а>0

а<0

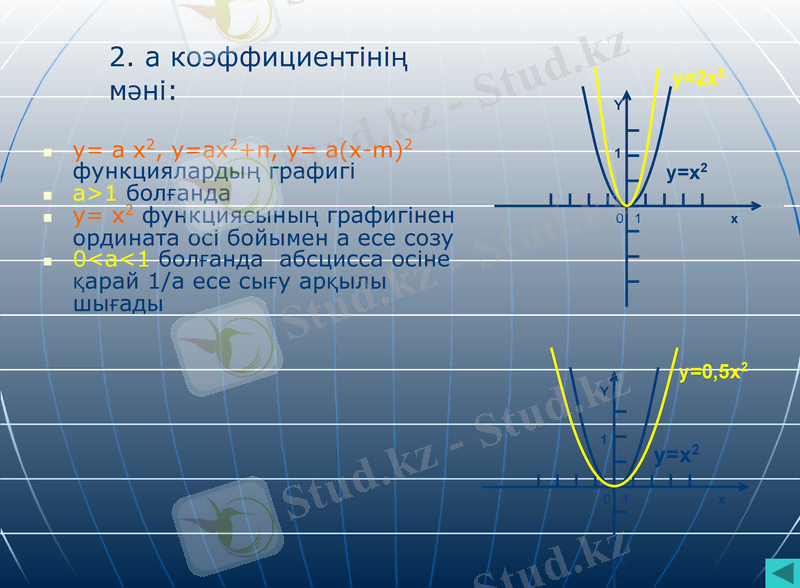
y= а х2, y=ах2+n, y= а(х-m) 2 функциялардың графигі

а>1 болғанда

y= х2 функциясының графигінен ордината осі бойымен а есе созу

0<а<1 болғанда абсцисса осіне қарай 1/а есе сығу арқылы шығады

0 1 x

y=x2

y=2x2

0 1 x

y=x2

y=0, 5x2

2. а коэффициентінің мәні:

4. y= ax2+n функциясының графигін

қалай салуға болады ?

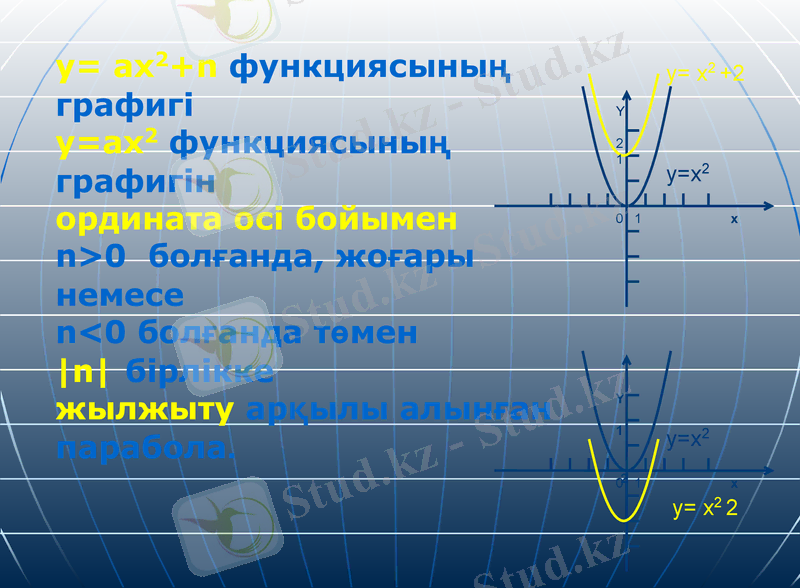
y= ax2+n функциясының графигі

y=ax2 функциясының графигін

ордината осі бойымен

n>0 болғанда, жоғары немесе

n<0 болғанда төмен

n бірлікке

жылжыту арқылы алынған парабола.

0 1 x

y= x2 +2

y=x2

0 1 x

y= x2 2

y=x2

-2

5. y= a(x-m) 2 функциясының

графигін

қалай салуға болады?

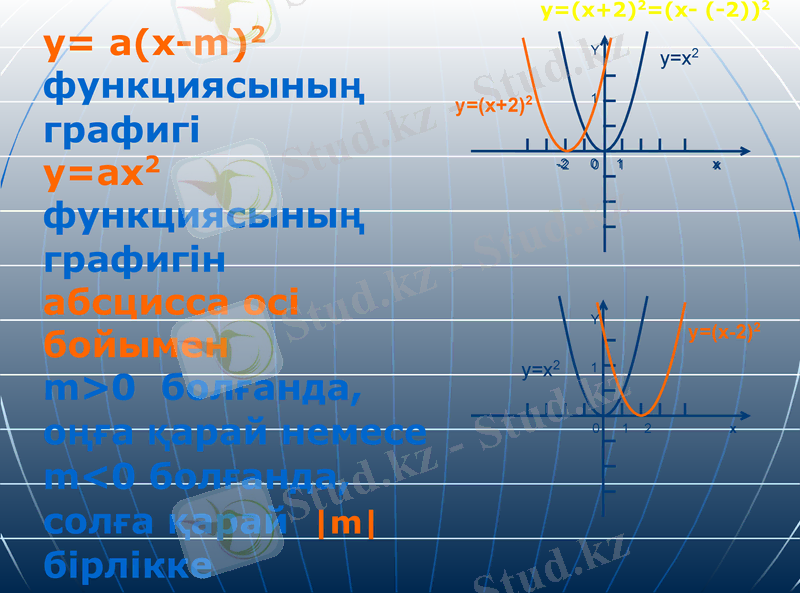
y= a(x-m) 2 функциясының графигі

y=ax2 функциясының графигін

абсцисса осі бойымен

m>0 болғанда,

оңға қарай немесе m<0 болғанда, солға қарай m бірлікке

жылжыту арқылы алынған парабола.

-2 0 1 x

y=x2

y=(x+2) 2

0 1 2 x

y=x2

y=(x-2) 2

y=(x+2) 2=(x- (-2) ) 2

-2 0 1 x

6. y= a(x-m) 2+n

функциясының графигін

қалай салуға болады ?

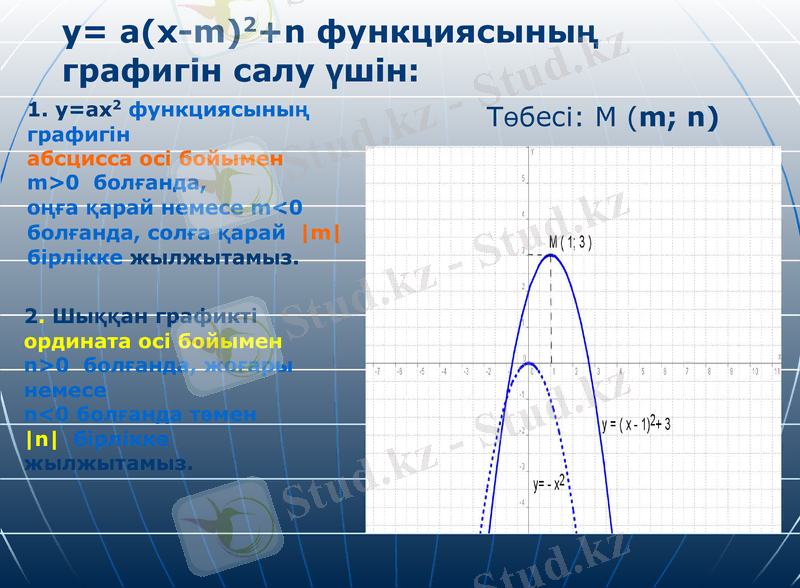
1. y=ax2 функциясының графигін

абсцисса осі бойымен

m>0 болғанда,

оңға қарай немесе m<0 болғанда, солға қарай m бірлікке жылжытамыз.

2. Шыққан графикті

ордината осі бойымен

n>0 болғанда, жоғары немесе

n<0 болғанда төмен

n бірлікке

жылжытамыз.

y= a(x-m) 2+n функциясының

графигін салу үшін:

Төбесі: М (m; n)

Ауызша есептер шығару

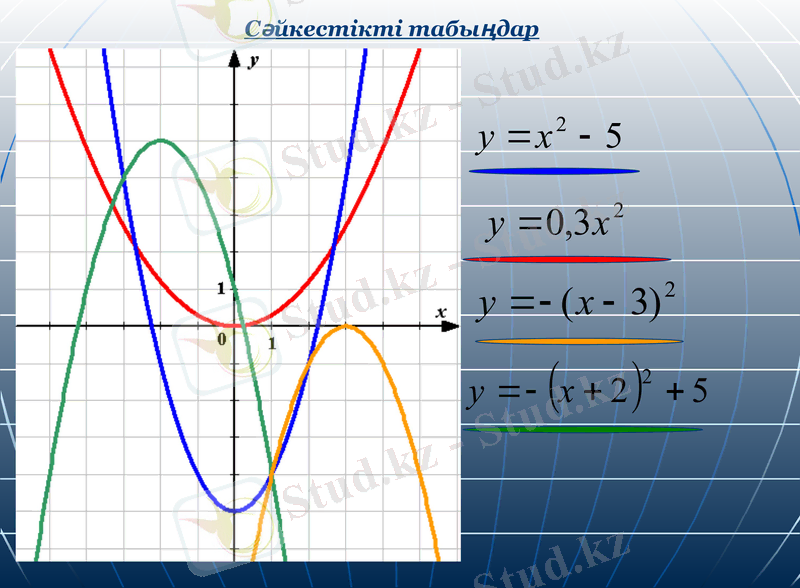
Сәйкестікті табыңдар

Квадраттық функция келесі формуламен берілген. Парабола төбесін анықтаңдар.

y = x2 -6

y = (x-5) 2

y = (x-7) 2 +4

y = (x+3) 2 -1

(0; -6)

(5; 0)

(7; 4)

(-3; -1)

y= 0, 5(x-1) 2+4 функциясының графигін

y=0, 5x2 функциясының графигінен

қалай алуға болады?

Aбсцисса осі бойымен 1бірлікке оңға жылжытамыз, өйткені m=1. Нәтижесінде 0, 5(х-1) 2 функциясының графигін аламыз.

Шыққан графикті ордината осі бойымен

4 бірлікке жоғары жылжытамыз, өйткені n=4

Шыққан парабола y= 0, 5(x-1) 2+4 функциясының графигі болады.

тапсырманы

тексеру

Шығармашылық

y= ‌ x2 - 2 ‌

функциясының

графигін

салу

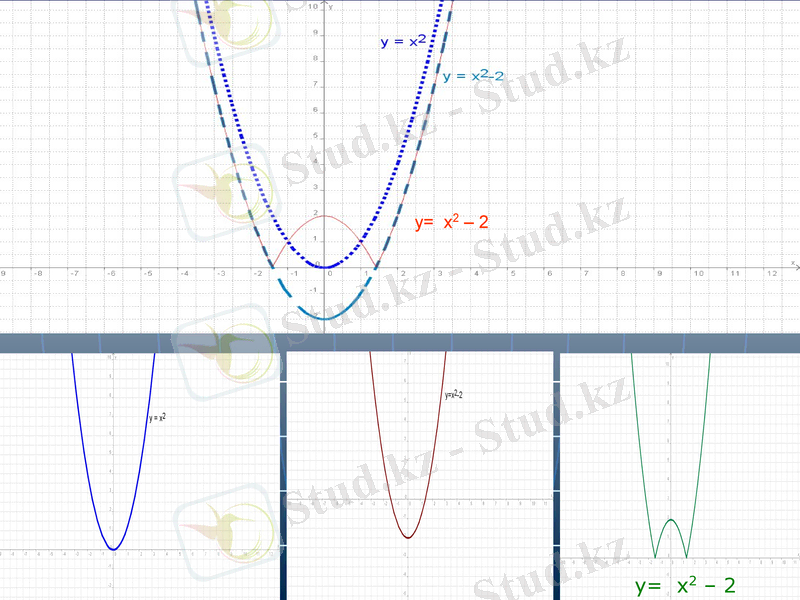
y= ‌ x2 - 2 ‌

y=-(x-3) 2+1

функциясының графигін салу

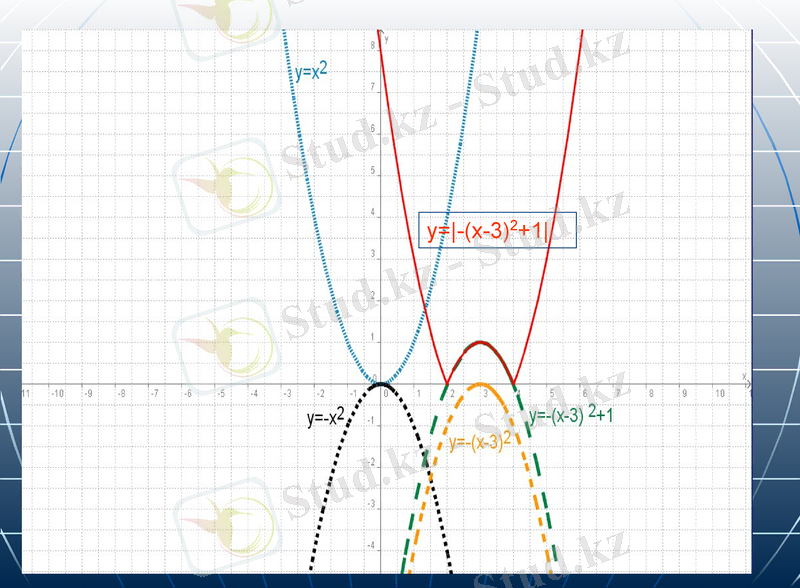
y=-(x-3) 2+1

Практикалық жұмыс

y=x2 үлгісінің көмегімен :

а) y=-x2-2 ә) y=-(х+1) 2 - 3

б) y=-х2 +3 графиктерін салыңдар?

2. Салуды орындамай-ақ, функцияның графигінің х осімен және у осіменен қиылысу нүктелерінің координаталарын табыңдар:

а) y=х2+2х ә) y=х2 +2х-8

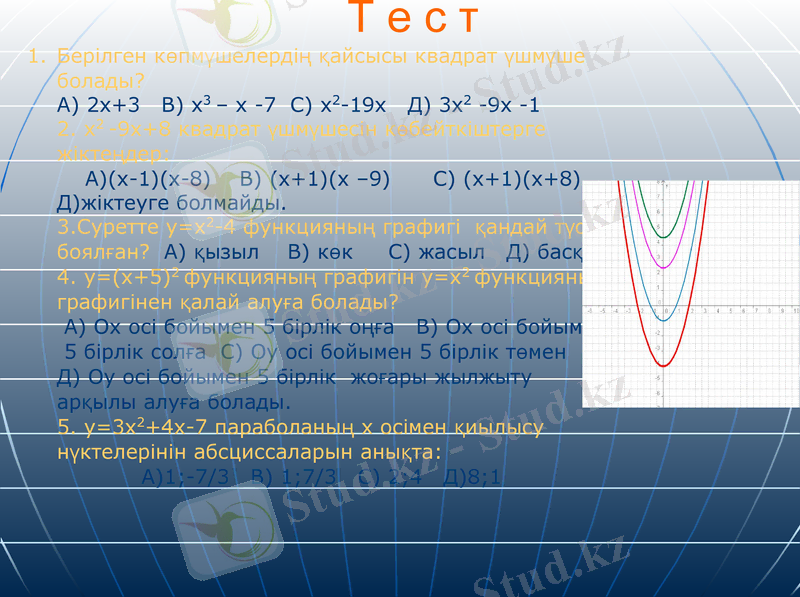
Т е с т

Берілген көпмүшелердің қайсысы квадрат үшмүше болады?

А) 2х+3 В) х3 - х -7 С) х2-19х Д) 3х2 -9х -1

2. х2 -9х+8 квадрат үшмүшесін көбейткіштерге жіктеңдер:

А) (х-1) (х-8) В) (х+1) (х -9) С) (х+1) (х+8) Д) жіктеуге болмайды.

3. Суретте y=x2-4 функцияның графигі қандай түске боялған? А) қызыл В) көк С) жасыл Д) басқа

4. y=(x+5) 2 функцияның графигін y=x2 функцияның графигінен қалай алуға болады?

А) Ох осі бойымен 5 бірлік оңға В) Ох осі бойымен

5 бірлік солға С) Оу осі бойымен 5 бірлік төмен

Д) Оу осі бойымен 5 бірлік жоғары жылжыту арқылы алуға болады.

5. y=3x2+4х-7 параболаның х осімен қиылысу нүктелерінін абсциссаларын анықта:

А) 1; -7/3 В) 1; 7/3 С) 2; 4 Д) 8; 1

Дұрыс жауаптар:

1. Д

2. А

3. А

4. В

5. А

Үйге деңгейлік тапсырма:

№ 253

№257

№262

Ұқсас жұмыстар

Функция графиктерін түрлендіру: параллель көшіру және салу алгоритмі

Квадраттық функциялар: парабола графигі, қасиеттері және тапсырмалар

Квадраттық функциялар: жіктеу, график трансформациялары және тесттік тапсырмалар

Квадраттық теңдеулер: анықтамалар, түрлері және есептер

Көп айнымалы функциялар: анықталу облысы, шегі мен үзіліссіздігі, дербес туындылар және толық пен жоғары ретті дифференциалдар

y = ax^2 және y = a(x - m)^2 функцияларының анықтамасы және графиктерін түрлендіру

Десмургия: таңғыштардың түрлері мен салу принциптері

Квадраттық теңсіздіктерді графиктік тәсілмен шешу

Десмургия: таңғыш материалдары, таңу түрлері мен салу әдістері

Десмургия: таңғыштар мен байламдардың түрлері және салу техникасы

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz