Теңдеулерді шешудің жалпы әдістері



Теңдеулер шешудің жалпы әдістері
Ақтөбе қаласы
Елек орта мектебі
11-класс
Математика пәні мұғалімі
Бижанов Б.
1

Сабақ мақсаты
Білімділік: теңдеудің түрлері, теңдеулер шешудің негізгі тәсілдері бойынша білімдерін жалпылау, “салдар-теңдеу” ұғымымен танысу
Тәрбиелік: ізденімпаздыққа, жаңашылдыққа тәрбиелеу
Дамытушылық: теңдеуді түрлендірудің, түбірлерін тексерудің дағдысын қалыптастырып, білім, біліктерін жетілдіру
2
3

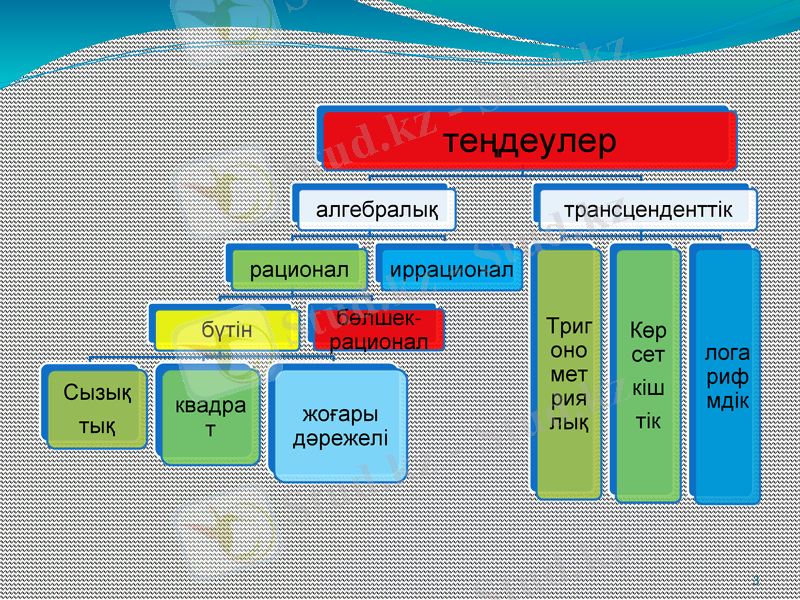
Салдар-теңдеу
Теңдеуді түрлендіргеннен кейін пайда болған теңдеу берілген теңдеуге қатысты салдар-теңдеу деп аталады.
4

Мысал. = х теңдеуін қарастырайық, оны түрлендіргеннен кейін х2+х-6=0 теңдеуін аламыз. Соңғы теңдеудің түбірлері -3 және 2. 2-бірінші теңдеудің түбірі болады. ал -3 түбірі емес, яғни бұл екі теңдеу нақты сандар жиынында мәндес емес.
Қорытынды: егер берілген теңдеу салдар-теңдеу арқылы шығарылса, онда салдар-теңдеудің барлық түбірі бастапқы теңдеудің түбірі болатынын тексеру керек.
5

Салдар-теңдеуге келтірілетін түрлендірулер
1. Теңдеуді натурал дәрежеге келтіру 2. Теңдеуді логарифмдеу және потенциалдау
3. Теңдеуді бөлімдерінен босату
4. Формулаларды қолдану
5. Бірнеше түрлендірулерді қолдану
6

1. Теңдеуді натурал дәрежеге келтіру = екі жағын да квадраттап, х2-7х+10=0 салдар-теңдеуін аламыз. Оның түбірлері 2 және 5. Тексерсек, 2- түбір бола алмайды, ал 5-түбір болады. Жауабы: 5
Қорытынды: егер теңдеуді тақ дәрежеге шығарсақ, оған мәндес салдар -теңдеу шығады.
Егер жұп дәрежеге шығарсақ, барлық жағдайда оған мәндес салдар-теңдеу шыға бермейді.
7

2. Теңдеуді логарифмдеу және потенциалдау
2-мысал. Log4 (х2-5х) = Log4 (х-9) теңдеуін шешейік.
Мүмкін мәндер жиыны - (9; ∞) . Енді берілген теңдеуді потенциалдасақ, х2-5х=х-9 салдар-теңдеуін аламыз. Оның түбірі х=3. Бұл түбір мүмкін мәндер жиынына тиісті емес. Сондықтан берілген теңдеудің түбірі болмайды.
Жауабы: түбірі жоқ.
Қорытынды: салдар-теңдеудің түбірлерінің
мүмкін мәндер жиынына тиістілігін тексеру керек.
8

3. Теңдеуді бөлімдерінен босату
3-мысал. =
Анықталу облысы х ≠ 1, х ≠-5.
Пропорция қасиетін қолданып, 2х2+7х-15=0
салдар-теңдеуін аламыз. Түбірлері 1, 5 және -5.
Жауабы: 1, 5
Қорытынды: салдар-теңдеудің түбірлерінің
анықталу облысына тиістілігін тексеру керек.
9

4. Формулаларды қолдану
4-мысал. Log5(3х2+4х-1)
5 = 2х2-4. Бұдан шығатын салдар-теңдеу х2+4х+3=0. Түбірлері -1 және -3.
Мүмкін мәндер жиынын ескерсек, -1 бөгде түбір.
Жауабы: -3
10

5. Бірнеше түрлендірулерді қолдану
= теңдеуін шешейік.
Теңдеудің екі жағын да квадраттап, ықшамдасақ,
= 6 теңдеуін аламыз, тағы да екі жағын квадраттап х2+7х-30=0 салдар-теңдеуін аламыз.
Оның түбірлері 3 және -10. Тексерсек, -10 бөгде түбір екенін көреміз.
Жауабы: 3
11

Түрлендіру кезінде түбірлердің жоғалуы
Мысал. 2х(х-1) = 5(х-1) теңдеуін шешейік.
1-жағдай. Теңдеудің екі жағын да ( х-1 ) -ге қысқартсақ, 2х=5. Бұдан х = 2, 5
2-жағдай. Жақшаны ашайық : 2х2-2х=5х-5, бұдан 2х2-7х+5=0 салдар-теңдеуі шығады.
Оның түбірлері 1 және 2, 5
Жауабы: 1 және 2, 5
Қорытынды: теңдеудің екі жақ бөлігін айнымалысы бар көбейткішке қысқарту түбірлердің жоғалуына әкелуі мүмкін.
12

Ауызша тапсырмалар
Теңдеудің түрін анықтап, түбірін тап.
1. 2х+6= 17. 2. =0. 3. (х-3) (х+5) =0.
4. х2-х-12=0. 5. 3х2-8х+5=0. 6. = х
Теңдеуді шешіп, х1+х2+х1х2 мәнін есепте:
1. х2+7х+12=0
2. 2х2-9х+7=0
13

Бекіту есептері
1) . 5 + = х ; 2) . ( ) =0;
3) . = ; 4) . = ;
5) . - =5 ; 6) . х∙Log3(Cos(π-х) ) =0;
7) . -1 = ; 8) . Logх(х2-2х+2) =1;
14

Бекіту есептері
Теңдеулерді шешіңдер:
9. (3Lgх+2) /(1-Lg2х) =1/(1-Lgх) ;
10. Log2(11-х) +1 = Log2182 -2Log2√(5-х) ;
15

Үй тапсырмасы
§20 № 330, 337
16

Назарларыңызға рахмет!
Сау болыңыздар!
17
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz