Теңдеулер жүйесін шешу

Презентация қосу

№ 84 Циолковский атындағы жалпы орта
мектеп

қолданбалы курс

Сабақтың тақырыбы: “Модуль
таңбасы бар теңдеулерді шешу”

Орындаған: Қарабалаева Салтанат
Шымкент
қаласы
ТҮСІНІК ХАТ

«Модуль таңбасы бар теңдеулерді шешу» -10 «б» сынып, қолданбалы курс

10-11 сыныптардағы жаратылыстану – математикалық бағыттағы математика курсында
қосымша түрде қолданбалы курсы қарастырылады. 10 «б» сыныбына математикадан
қолданбалы таңдау курсында санның модулі туралы ұғым және оның қасиеттерін пайдаланып
теңдеулер және теңсіздіктер шешуді таңдап алдық. Себебі, ҰБТ-да математикадан берілетін
есептердің ішінде модуль таңбасы бар теңдеулер және теңсіздіктерді шешу көптеп кездеседі.
Бірақ бұл тақырыптың есептерін шешуге мектеп бағдарламасында сағат бөлінбеген. Сондықтан
модуль таңбасы бар теңдеулер мен теңсіздіктерді шешудегі оқушылардың білімдері саяз
болғандықтан ондай есептерді шешуде қиындыққа кездеседі. Сол мақсатпен осы тақырыпты
таңдап алдым.
Таңдау курсына бағдарлама бойынша 34 сағат берілген. Бағдарлама төрт тараудан тұрады:
I тарау. Модуль таңбасы бар теңдеулерді шешу.
II тарау. Модуль таңбасы бар теңсіздіктерді шешу.
III тарау. Модуль таңбасы бар трансиденттік теңдеулерді және теңсіздіктерді шешу.
IV тарау. Модуль таңбасы бар функциялардың графиктерін салу.
Қолданбалы курстағы есептердің мазмұны, оқулықтағы және ҰБТ- дағы есептер. Есептердің
шығарылу жолдары алдымен әртүрлі тәсілдермен көрсетіліп, ал қалған есептерді
оқушылардың өздіктерінен тиімді тәсілді таңдап алуына баса назар аударту керек. Есептерді
шешуде олардың теориялық түсініктемелері басшылыққа алынып практикада толықтырылып
отыру керек.
Бұл таңдау курсының мақсаты мен міндеті жаратылыстану-математикалық бағыттағы оқитын
оқушылардың білімдерін кең түрде тереңдетіп жүйелі түрде өздіктерінен табысты нәтижелі
білім алуға бағыттау.

ТАҢДАУ КУРСЫНЫҢ МАҚСАТТАРЫ
МЕН МІНДЕТТЕРІ

Жаратылыстану – математикалық бағыттағы мектептердің жоғарғы
сатысында математиканы оқытудың мақсаттары мен міндеттері.
• оқушыларды модель құруға;
• қойылған мәселені шешу үшін қажетті алгоритмді құруға;
• ыңғайлы математикалық әдістерді таңдауға үйрету;
• эксперименттік жұмыстарды орынды жүргізу және есептеу, өлшеу;
• зерттеу нәтижелеріне математикалық тұрғыда баға бере білу;
• өз бетінше білім алу қабілеттерін дамыту;
• математикалық ойлауды тереңдету;
•оқушылардың математикалық қабілеттерін, іздену дағдыларын арттыру;
• ғылыми – көпшілік әдебиеттерді өз беттерімен пайдалана білуге үйрету;
•математиканы ғылым мен техникада, өмірде пайдалана білу тағы басқа
мақсаттарға жетуін көздейді.

КУРСТАН КҮТІЛЕТІН
НӘТИЖЕ
Ғылым мен техниканың жедел қарқынмен дамуы мектеп математика
курсын оқытуда көптеген жаңа сауалдар қойды. Ғылыми техниканы
математикаландыру кезеңінде, халық шаруашылығына математикадан
жан-жақты дайындалған қабілетті жастарды қажет етіп отыр. Осы
себепті оқушылардын математикаға қызуғушылығын арттыру
мақсатында жаратылыстану- математикалық бағыттағы оқитын
мектептердін жоғарғы сатысында математикадан қолданбалы таңдау
курсына қосымша сағат бөлінді. Бұл таңдау курсында оқу материалы
тереңдетіледі және кейбір тақырыптар кеңейтіледі, оқытылған
теориялардың практикалық қосымшаларымен таныстыру өрісі ұлғаяды.
Қиындығы жоғары мазмұндағы есептер көптеп шығарылады. Арнайы
оқулықтармен қатар қосымша әдебиеттер кеңінен қолданылады.
Қарапайым сыныптармен салыстырғанда таңдау курсы оқытылған
оқушылардың математиканы оқып үйренуде әр түрлі қосымша
әдебиеттерді пайдаланып өздіктерінен жұмыс істеуге талаптанып
дағдыланады, математикалық білім деңгейін арттыруға бағыттайды.
Таңдау курсына қойылған негізгі талап- оқушыларды қалаған
мамандықтарына сәйкес жоғарғы оқу орнына түсуге әзірлеу, ҰБТ-да
жоғары нәтижелер алуға білімдерін ұшқырлау.
«Модуль таңбасы бар теңдеулерді шешу»10 «б»
сынып қолданбалы курсттың тақырыптық
жоспары.
№ Сабақтың тақырыбы Сағат Мерзімі
саны
І І тарау. Модуль таңбалары бар теңдеулерді
шешу.
1 Санның модуліне анықтама және оны 1 01.09.10
пайдаланып өрнектердің мәнін шешу
2 Модуль және түбірі бар өрнектерді түрлендіру. 1 08. 09.10
3 Модуль таңбасы бар теңдеулерді 1 15. 09.10
геометриялық тәсілімен шешу.
4 Модуль таңбасы бар теңдеулерді квадраттау 1 22. 09.10
тәсілімен шешу.
5 Модуль таңбасы бар теңдеулерді модулдьдің 1 29. 09.10
анықтамасын пайдаланып шешу
6 Модуль таңбасы бар теңдеулерді интервалдар 1 06. 10.10
әдісімен шешу.
7 Модуль таңбасы бар теңдеулерді модульдің 1 13. 10 .10
негізгі қасиеттерін пайдаланып шешу
8 Модуль таңбасы бар теңдеулер жүйесін шешу 1 20. 10.10
9 Есептер шығару. I тарауды қайталау 1 27. 10.10
1 Сынақ алу №1 1 03. 11.10
0
№ Сабақтың тақырыбы Сағат Мерзімі
саны

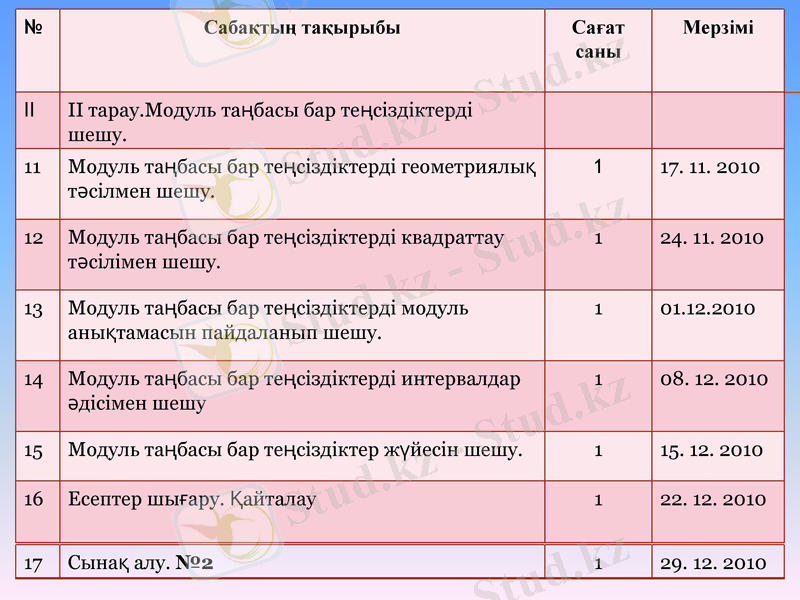
II II тарау.Модуль таңбасы бар теңсіздіктерді
шешу.
11 Модуль таңбасы бар теңсіздіктерді 1 17. 11.
геометриялық тәсілмен шешу. 2010

12 Модуль таңбасы бар теңсіздіктерді 1 24. 11.
квадраттау тәсілімен шешу. 2010

13 Модуль таңбасы бар теңсіздіктерді модуль 1 01.12.2010
анықтамасын пайдаланып шешу.

14 Модуль таңбасы бар теңсіздіктерді 1 08. 12.
интервалдар әдісімен шешу 2010

15 Модуль таңбасы бар теңсіздіктер жүйесін 1 15. 12.
шешу. 2010
16 Есептер шығару. Қайталау 1 22. 12.
2010

17 Сынақ алу. №2 1 29. 12.
2010
№ Сабақтың тақырыбы Сағат Мерзімі
саны
III III тарау. Модуль және трансиденттік
теңдеулерді, теңсіздіктерді шешу
18 Модульді пайдаланып иррационал 1 12. 01.11
теңдеулер шешу.
19 Есептер шығару. 1 19. 01.11
20 Модуль таңбасы бар тригонометриялық 1 26. 01.11
теңдеулерді шешу.
21 Есептер шығару. 1 02.02.11
22 Модуль таңбасы бар тригонометриялық 1 09. 02.11
теңсіздіктерді шешу.
23 Есептер шығару. 1 16. 02.11
24 Модуль таңбасы бар логарифм теңдеулерді 1 23. 02.11
шешу.
25 Модуль таңбасы бар логарифм 1 02.03.201
теңсіздіктерді шешу. 1
26 Есептер шығару. 1 09. 03.11
27 Сынақ алу . №3 1 16. 03.11
№ Сабақтың тақырыбы Сағат Мерзімі
саны
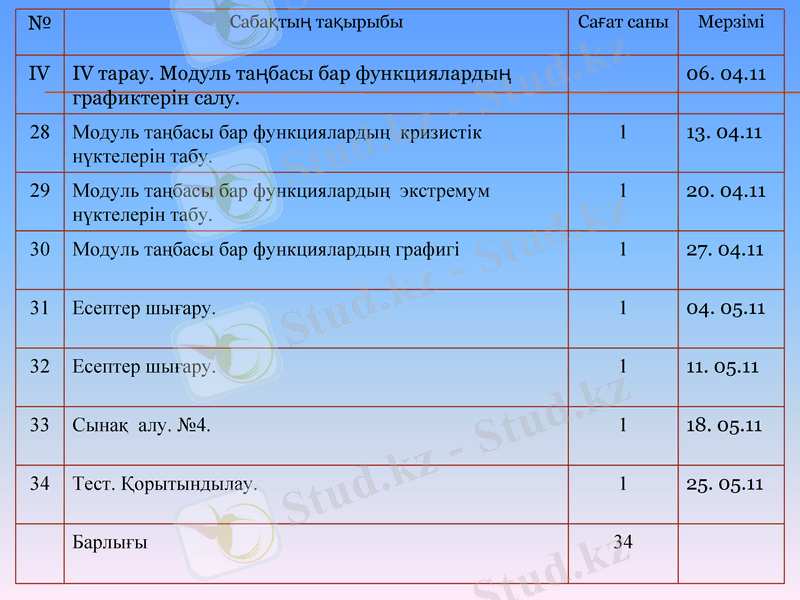
IV IV тарау. Модуль таңбасы бар 06.
функциялардың графиктерін салу. 04.11
28 Модуль таңбасы бар функциялардың кризистік 1 13.
нүктелерін табу. 04.11
29 Модуль таңбасы бар функциялардың экстремум 1 20.
нүктелерін табу. 04.11
30 Модуль таңбасы бар функциялардың графигі 1 27.
04.11
31 Есептер шығару. 1 04.
05.11

32 Есептер шығару. 1 11.
05.11

33 Сынақ алу. №4. 1 18.
05.11

34 Тест. Қорытындылау. 1 25.
05.11
Модуль таңбасы бар
теңдеулерді шешу тәсілдері
Айнымалысы модуль таңбасымен берілген теңдеулерді модуль таңбасы бар теңдеулер деп
аталады.Модуль таңбасы бар теңдеулерді шешудің бірнеше тәсілдері бар. Оларды мысалдар
арқылы қарастырайық. 1-мысал.|x -1|=2
Шешуі: 1-тәсіл. |x-1|=2(Геометриялық тәсіл).
|х-а|=2 өрнегінің геометриялық мағынасы – ол сан осіндегі х нүктесінен а нүктесіне дейінгі
қашықтықты білдіреді. Онда |х-1|=2 теңдеуінің геометриялық мағынасы х және 1 нүктелерінің ара
қашықтығы 2-ге тең болатындығында. Олай болса, х=-1 немесе х=3 болуы керек.

◦ • • • ◦ х Жауабы:-1; 3
-1 1 3
2-тәсіл. (Квадраттау тәсілі).Берілген теңдеудің екі жақ бөлігі де оң болғандықтан, оны
квадраттап, х2-2х+1=4 немесе x2-2х-3=0 квадрат теңдеуін аламыз. Оның түбірлері:x=-1 және
x=3.
3-тәсіл.(Анықтама тәсілі).Анықтама бойынша

a=

Нақты сандардың модулының анықтамасын және нақты сандар қасиетерін пайдаланып,
құрамында модулы бар теңдеулерді шешу модулы жоқ теңдеулерді шешуге келтіреді.
I. │f(x)│=a түріндегі теңдеулерді шешу. Модуль анықтамасы бойынша бұл
теңдеуді шешу келесі екі теңдеуді шешумен бірдей:

f(x) = [
Мұндағы, бірінші теңдеудің шешімдер жиыны {х1},екінші теңдеудің шешімдер
жиыны {х2} болса, берілген теңдеудің шешімдері осы екі жиының бірігуі болады :
{х}={х1} U{х2}
1-мысалдағы |х-1|=2 теңдеуін анықтама тәсілімен шешейік: x- 1=2 x -1=-2

х1=3 х2 = -1
Жауабы: -1; 3
II. f(|x|)=a түріндегі теңдеуді шешу.
Модуль анықтамасы бойынша берілген теңдеу екі аралас жүйеге
ажырайды:
немесе
f(|x|) функциясы жұп функция болғандықтан оның шешімдері жұптас
қарама-қарсы сандар болады, басқаша айтқанда, егер k берілген
теңдеудің шешімі болса - k де оның шешімі болады. Демек, осы
жүйелердің біреуін шешу жеткілікті.
2-мысал: |x|=2x2-1 Шешуі. немесе
Алғашқысын шешу жеткілікті х=1, демек х2 =-1 Жауабы:±1
3-мысал: х2-2|x|=0 Шешуі: немесе
Бірінші жүйені шешеміз.
x(x-2)=0 х1=0 және х2=2 түбірлерін алсақ, онда екінші
жүйенің шешімі
0 және -2 болғаны. Демек шешімдері:±2 және 0
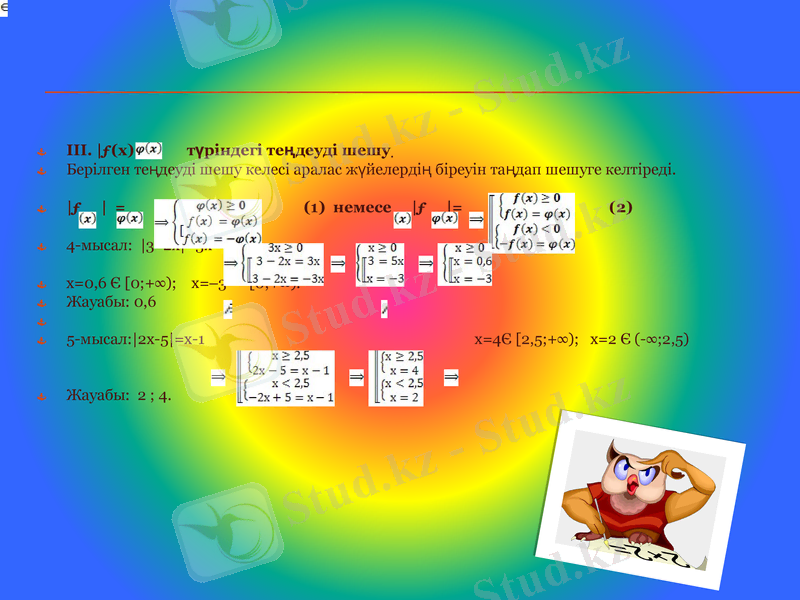
III. |ƒ(х) |= түріндегі теңдеуді шешу.
Берілген теңдеуді шешу келесі аралас жүйелердің біреуін таңдап шешуге келтіреді.

|ƒ | = (1) немесе |ƒ |=
(2)

4-мысал: |3‒2x|=3x

х=0,6 Є [0;+∞); x=‒3 [0;+∞).
Жауабы: 0,6

5-мысал:|2х-5|=x-1 х=4Є [2,5;+∞); х=2 Є (-
∞;2,5)

Жауабы: 2 ; 4.
IV. | k1x+b1|+|k.2x+b2|+..............|knх+bn|=a түріндегі теңдеуді шешу. (Аралықтар әдісі).
Теңдеудің сол жақ бөлігіндегі модуль астындағы өрнектерді нольге айналдыратын сандарды
табамыз. Оларды критикалық нүктелер деп атайды.
=- x₂= - xn = -

Айталық , ................... болсын.
Координаталық түзуді (‒ ,[ x₂;х3),.....,[ xn,+ ) аралықтарына бөлшектеп, аралықтар
әдісімен осы аралықтардағы бастапқы теңдеудің шешімдері бары жоқтығы анықталады.
(‒ бастапқы теңдеу f₁(x)=0 сызықтық теңдеуіне түрленеді. Мұның түбірі х=k₁
делік. Егер k₁(‒ болса, онда k₁ бастапқы теңдеудің шешімі болады. ал егер k₁ (‒
Жоғарыдағы сияқты [x1; x2) аралығында бастапқы теңдеу f2(x)=0 сызықтық теңдеуіне түрленеді.
Оның түбірі х=k2 туралы да осының алдындағы сияқты тұжырымдар жасай аламыз. Осылай
аралықтарды біртіндеп қарастырып, ақырында fn+1(x)=0 теңдеуі мен оның түбірі х=kn+1
табамыз.Бұның да шешімі не шешімі еместігі анықталады.
Бастапқы теңдеудің шешімдер жиыны осылайша дербес аралықтардағы шешімдер жиынынан
тұрады.
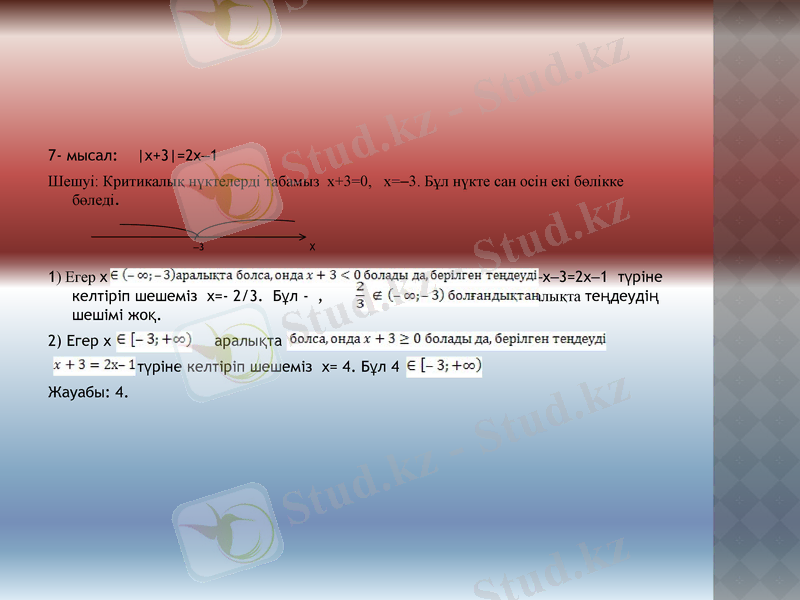
7- мысал: |x+3|=2x‒1
Шешуі: Критикалық нүктелерді табамыз x+3=0, x=‒3. Бұл нүкте сан осін екі бөлікке
бөледі.

‒3 Х

1) Егер x ‒x‒3=2x‒1
түріне келтіріп шешеміз x=- 2/3. Бұл - , бұл
аралықта теңдеудің шешімі жоқ.
2) Егер x аралықта
түріне келтіріп шешеміз x= 4. Бұл 4
Жауабы: 4.
ЕСЕПТЕР ШЫҒАРУ
I.Геометриялық тәсілмен шығарайық
№1. |х+4|=0 |х-(-4)|=0 х=-4+0=-4
Жауабы: - 4.

№2. |х-5|=3 х=5-3=2 х=5-(-3)=8
| • I х
2 5 8
Жауабы:(2;8)
№3. |х+5|=-3 |a| екенін
ескерсек, теңдеудің шешімі жоқ.
Жауабы:
№4. |х+1|=-3х |a| екенін ескерсек, х
х=-1-3х х=-1+3х
х=-0,25 х=0,5 шешімі
жоқ.
Жауабы: -0,25

№10. |х+2|=|х-1|
х= х=
2 х=-1 0•х

х=-0,5 х=
Жауабы: - 0,5
II. КВАДРАТТАУ ТӘСІЛІМЕН
ШЫҒАРАЙЫҚ

№11. |4-х|=|2х+1|
16-8х+х2=4х2+4х+1
3х2+12х-15=0 х2+4х-5=0
х1=-5; х2=1.
Жауабы: -5; 1.
№12. ||x|-2|=|x|
|х|2-4|х|+4=|х|2 ; 4|х|=4;
|х|=1; х= ± 1.
Жауабы: ± 1.
II. МОДУЛЬДІҢ АНЫҚТАМАСЫН
ПАЙДАЛАНЫП ТЕҢДЕУДІ ШЕШУ.

№15. ||x|–2|=4
|x|–2=4 |x|–2=–4
|x|=6 |x|=–2 шешімі жоқ
x=6 және x=–6
Жауабы:– 6;6

№20. |2х -

Жауабы:
IV. АРАЛЫҚТАР ӘДІСІМЕН
ШЕШУ.
№30. |х2-1|+|4+х2|= 5.
х2-1=0 , (х-1)(х+1)=0, х=1;
х=-1.
4+х2=0 , х2

1)
2)
3)

Жауабы: [-1;1].
V. МОДУЛЬДІҢ ҚАСИЕТТЕРІ.

№31.| 2х-7|+|х-3y+5|=0. Модулдің |a|
қасиетін пайдалансақ , онда берілген
теңдеу мына теңдеулер жүйесімен
мәндес болады.

Жауабы:
МОДУЛЬ ТАҢБАСЫ БАР
ЛОГАРИФМДІК ТЕҢДЕУЛЕР
ШЕШУ.
№ 42.| Анықталу облысы: х-
2>0 х>2
Берілген теңдеу төмендегі теңдеулер
жиынтығына мәндес:
|

Бұл түбірлер анықталу обылысына
тиісті. Жауабы:11; 2 .
МОДУЛЬ ТАҢБАСЫ БАР ТРИГОНОМЕТРИЯЛЫҚ ТЕҢДЕУЛЕРДІ ШЕШУ.

№ 53.

Екі түбірді біріктірсек х=
Жауабы:
МОДУЛЬДІ ПАЙДАЛАНЫП
ИРРАЦИОНАЛ ТЕҢДЕУЛЕРДІ ШЕШУ
№35 + =10

+ 10

Критикалық нүктелер х=4, х=0,5 · 0,5 ·4
х

шешімі жоқ.

Жауабы: ;5.
МОДУЛЬ ТАҢБАСЫ БАР КЕРІ
ТРИГОНОМЕТРИЯЛЫҚ ТЕҢДЕУЛЕРДІ ШЕШУ.

№ 56.

Жауабы: .
МОДУЛЬ ТАҢБАСЫ БАР
ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУ.
№ 60 Теңдеулер жүйесін шешу.

Сонда =| |=0,
Жауабы: (0;0), ( ; ).
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР
1) Гайдуков И. И. Абсолютная величина: Пособие для
учителей. 2-е изд.М., 1968.
2) Зильберберг Н.И. Алгебра для углубленного изучения
математики. Псков, 1992.
3) Литвененко В.Н., Мордкович А.Г. .Практикум по решению
математических задач: Алгебра. Тригонометрия. М., 1984.
4) Мордкович А.Г. Кое-что о радикалах // Квант. 1970. №3.
5) Спатару К. Абсолютная величина числа. Кишинев, 1966.
6) Шарыгин И.Ф. Факультативный курс по математике:
Решение задач:Учебное пособие для 10 класса средней
школы. М., 1989.
7) Анарбекова А., Ж. Бейсеков, Ж. Назанов, А. Таниргенов,
2007.
Сборник разноуровневых тестовых заданий для подготовки
к единому нациольному тестированию (ЕНТ) по алгебре
для поступающих в Вузы.
НАЗАРЛАРЫҢЫЗҒА РАХМЕТ!

Ұқсас жұмыстар

Сызықтық теңдеулер жүйесі және оның классификациясы

Теңдеулер мен теңдеулер жүйелерін шешу тақырыбына қайталау

Матрицалық шешім әдісі

Біртектес тригонометриялық теңдеулерді шешу

БІРТЕКТЕС СЫЗЫҚТЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУДІҢ ФУНДАМЕНТАЛДЫ ЖҮЙЕСІ

Тригонометриялық теңдеулер жүйесін шешу

Логарифмдік теңдеулерді шешу туралы ақпарат

Квадрат теңдеудің формуласын ата

Квадрат теңдеулерді шешу

Теңдеуді шешудің тәсілдері

Пәндер