Біртектес тригонометриялық теңдеулерді шешу

Презентация қосу

АШЫҚ
САБАҚ
Тригонометриялық
Тақырыбы:
теңдеулерді және теңдеулер
жүйесін шешу әдістеріне
есептер шығару
Топ: 5 «Тамақтандыруды
ұйымдастыру»
Курс: І
Пәні: Математика
Пән мұғалімі: Қасанова Гүлбаршын
Сабақтың мақсаты:
Білімділік: Тригонометриялық теңдеулерді
шешудің әртүрлі тәсілдерін білу,
біліктілігін арттыру.
Дамытушылық: Ойлау жүйесін сұрақтарға нақты
жауап беруге, тез шешім
қабылдауға дамытушылығын
арттыру.
Тәрбиелік: Оқушыларды тәрбиелей отырып,
үйрету, ізденімпаздыққа тәрбиелеу.
Үй жұмысын тексеру:№117(а
)
– қа бөлеміз.

0
=1,

х= , nєz.
Ауызша сұрақтар:
1. Тригонометриялық теңдеу деп нені айтады?
2. Қарапайым тригонометриялық теңдеу
дегеніміз не?
3. Тригонометриялық теңдеуді шешу дегеніміз
не?
4. y= sin x және y= cos x функциясына кері
функцияны қалай белгілейді және қалай оқиды?
5. Тригонометриялық теңдеулерді шешудің неше
жолы бар және атап айту керек?
Жауабы:
1. Айнымалысы тригонометриялық функция таңбасының ішінде болатын
теңдеу тригонометриялық теңдеу деп аталады.
2. sin x = а, , cos x= а , tg x= а, ctg x=a түрінде берілген теңдеу
қарапайым тригонометриялық теңдеу деп аталады.
3. Берілген теңдеуді тура тепе –теңдікке айналдыратын аргументтің
барлық мәндерін табу.
4. y=arcsin x, y= arccos x.
5. 6 жолы бар:
5.1. Тригонометриялық функциясының бір ғана түрлерімен берілген, алгебралық
теңдеулерге келтірілетін тригонометриялық теңдеулер
5.2. Тригонометриялық формулаларды түрлендіру жолымен шешілетін
тригонометриялық теңдеулер
5.3. Функциялардың дәрежесін төмендету арқылы шешілетін тригонометриялық
теңдеулер.
5.4. Біртектес тригонометриялық теңдеулерді шешу
5.5. Қосымша аргумент енгізу арқылы шығарылатын тригонометриялық теңдеулер.
5.6. Тригонометриялық теңдеулер жүйесін шешу.
ТОППЕН ЖҰМЫС
№ 115(А,В);
№113 (Ә);
а) 2sin2 x – 3 sin x +1 = 0
sin x = u, 2u2 – 3u + 1 = 0; D = 9 – 8 =1, u1 = 1, u2 = ½

sin x=1, x = + 2πn, nϵz. sin x = ½ , x=(-1)n + πn, nϵz

Жауабы: x = + 2πn, x=(-1)n + πn, nϵz

б) 6tg2 x + tg x -1 = 0
tg x = u, 6u2 + u - 1 = 0; D = 1+24 =25, u1 = ⅓ , u2 = -½

tg x= ⅓, x = arctg ⅓ + πn, nϵz. tg x = - ½ , x=arctg(- ½) n + πn, nϵz

ә) cos 5x + cos 3x = 0

2 cos 4x ∙ cos 3x = 0, cos 4x = 0, cos x = 0

4x= + πn. nϵz. x = , nϵz. cos x = 0, x = + πn. n ϵ z
Кеспе қағазбен
жұмыс

А -тобы
Б-тобы
В-тобы
С-тобы
Д-тобы
А - тобы:
1. α = 300 тең болғанда: sin α + cos α өрнегінің мәнін табу
керек
Жауабы:
2. 2 sin2 α + cos2 α – 1 – есептеңдер.
Жауабы: 2 sin2 α + cos2 α - sin2 α - cos2 α = sin2 α

Б – тобы:
1. Өрнекті ықшамдаңдар:
а) sin α ∙ ctg α = ? Жауабы: sin α ∙ = cos α

б) cos α - sin α ∙ ctg α = ? Жауабы: cos α - sin α ∙ =0
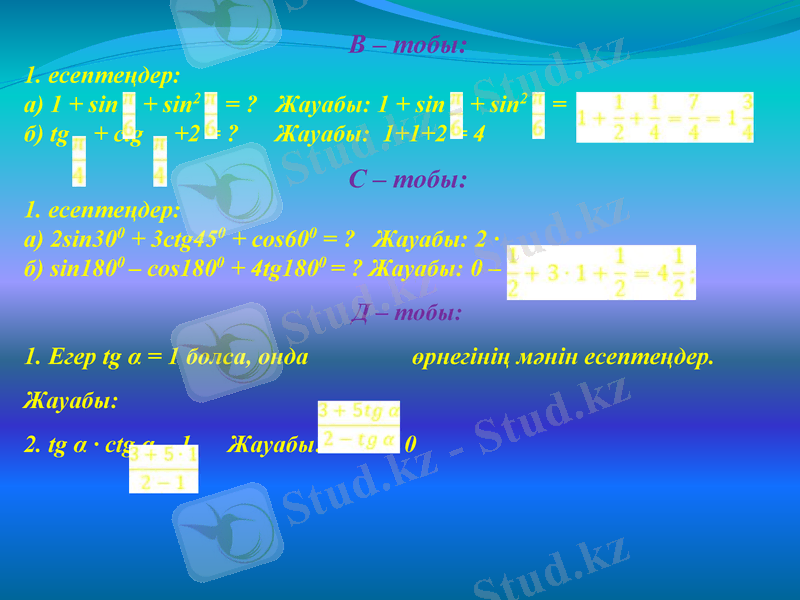
B – тобы:
1. есептеңдер:
а) 1 + sin + sin2 = ? Жауабы: 1 + sin + sin2 =

б) tg + ctg +2 = ? Жауабы: 1+1+2 = 4
C – тобы:
1. есептеңдер:
а) 2sin300 + 3ctg450 + cos600 = ? Жауабы: 2 ∙
б) sin1800 – cos1800 + 4tg1800 = ? Жауабы: 0 – (-1) + 4 ∙ 0 = 1

Д – тобы:

1. Егер tg α = 1 болса, онда өрнегінің мәнін есептеңдер.
Жауабы:

2. tg α ∙ ctg α – 1. Жауабы: 1 – 1 = 0
«Негізгі тригонометриялық тепе - теңдіктер»

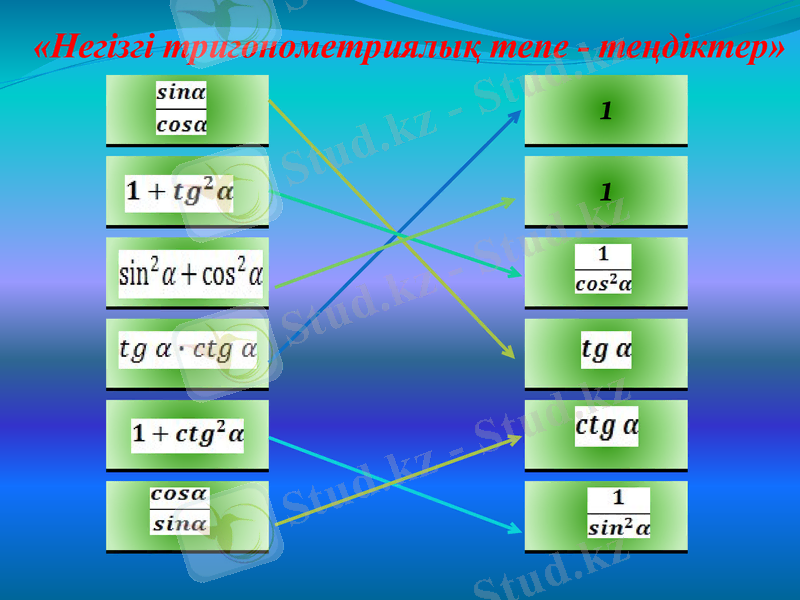
«Негізгі тригонометриялық тепе - теңдіктер»

Математикалық ойын
“ЛОТО”
Математикалық «лото» ойын.
sin x =а

cos x = а
|a| 1
|a| 1
болғанда
теңдеудің
шешімі tg x = а
жоқ.

ctg x
=
а

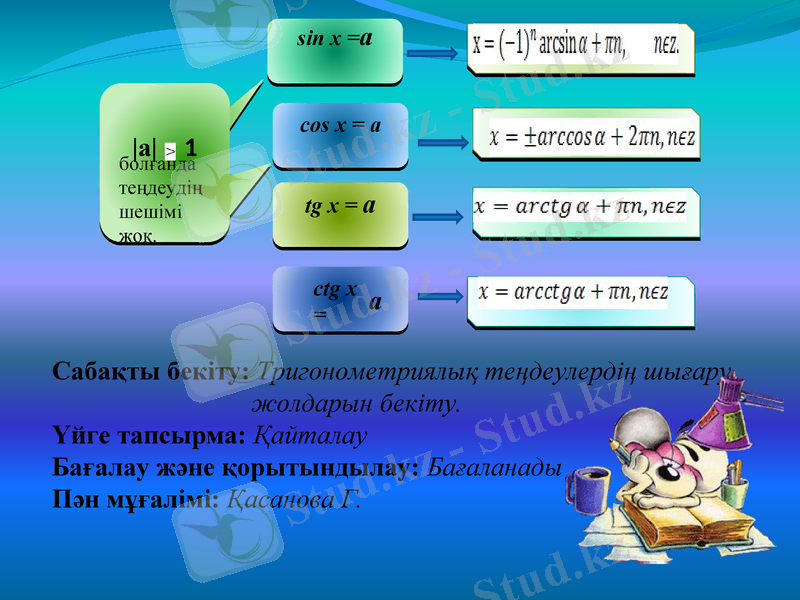
Сабақты бекіту: Тригонометриялық теңдеулердің шығару
жолдарын бекіту.
Үйге тапсырма: Қайталау
Бағалау және қорытындылау: Бағаланады
Пән мұғалімі: Қасанова Г.

Ұқсас жұмыстар

Тригонометриялық теңдеулер жүйесін шешу

Біртекті тригонометриялық теңдеу

Теңдеулер жүйесін шешу

Мектеп математикасындағы квадраттық теңдеулерді шешу жолдары

Тригонометриялық теңдеулерді шешу

Логарифмдік теңдеулерді шешу туралы ақпарат

Cos х = а, Sin х = а, tg х = а, ctg x = a түріндегі қарапайым тригонометриялық теңдеулер

Алгебралық есептерді шешудің геометриялық әдістері

Фотоматика калькуляторының көмегімен есептер шығару

Теңдеулер мен теңдеулер жүйелерін шешу тақырыбына қайталау

Пәндер