7-сынып геометриясы: циркуль мен масштабталмаған сызғышпен салу есептері мен дәлелдеулері



Геометрия - 7
Математика пәнінің мұғалімі Алматова Г. Ж.
Үш тілде оқытатын №21 орта мектеп-гимназия, Ақтөбе қаласы
Салу есептері

7 кластың геометрия курсында тек қана циркуль мен масштабы бөлінбеген сызғыштың көмегімен салуға болатын салу есептері қарастырылған.
Сызғыштың көмегімен кез-келген түзуді, берілген екі нүкте арқылы өтетін түзуді; ал циркулдің көмегімен кез-келген радиусты шеңбер жүргізуге және центрі берілген нүктедегі, радиусы берілген кесіндіге тең шеңбер жүргізуге болады.
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
А
В
С
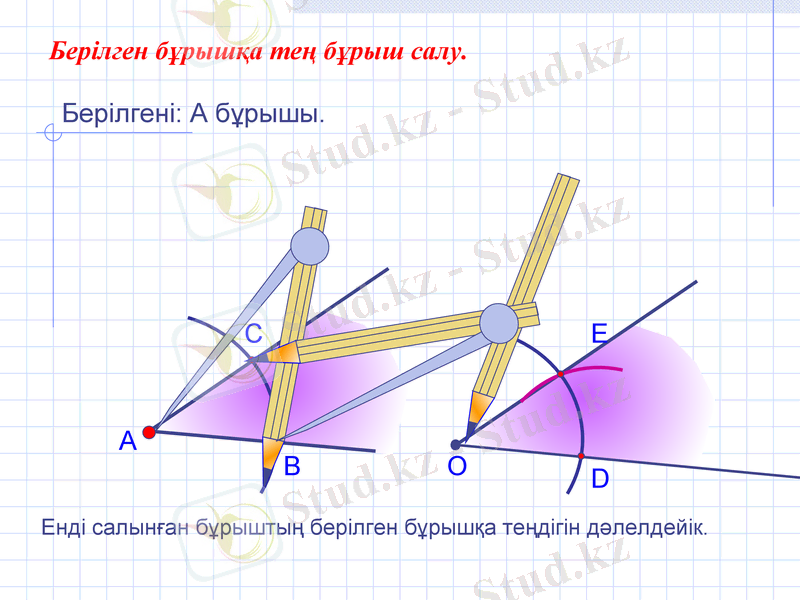
Берілген бұрышқа тең бұрыш салу.
Берілгені: А бұрышы.
О
D
E
Енді салынған бұрыштың берілген бұрышқа теңдігін дәлелдейік.
Берілген бұрышқа тең бұрыш салу.
Берілгені: А бұрышы.
А
О бұрышын салдық.
В
С
О
D
E
Ддәлелдеу керек: А = О
Дәлелдеуі: АВС және ОDE үшбұрыштарын қарастырайық.
АС=ОЕ, бірдей шеңберлердің радиустары.
АВ=ОD, бірдей шеңберлердің радиустары.
ВС=DE, бірдей шеңберлердің радиустары.
АВС= ОDЕ (3 белг. ) А = О
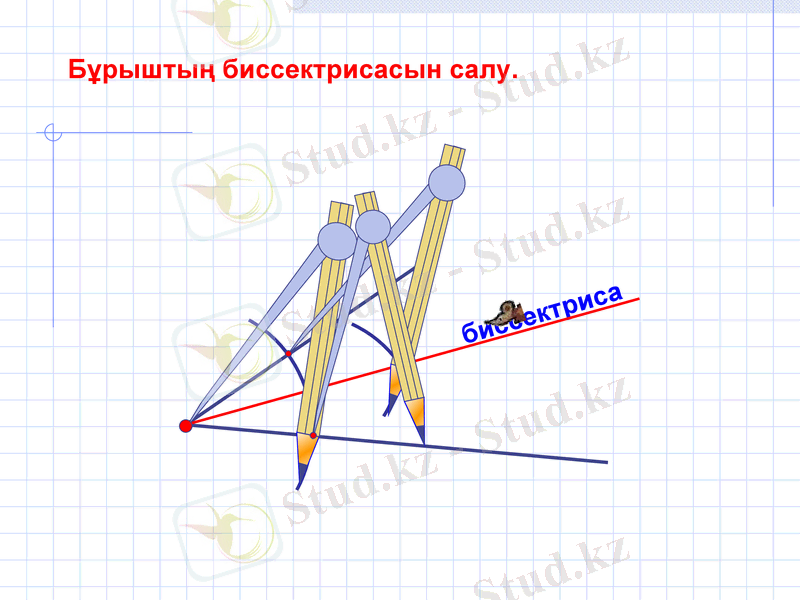
биссектриса
Бұрыштың биссектрисасын салу.
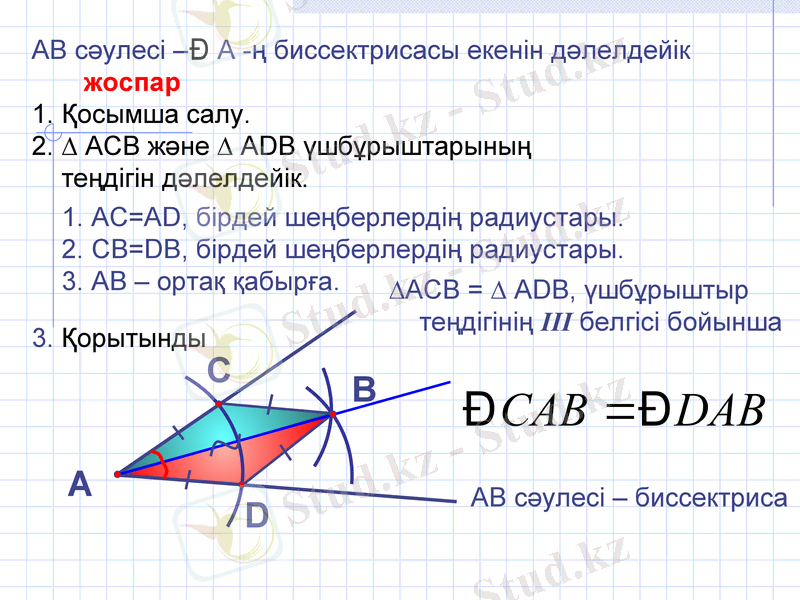
АВ сәулесі - А -ң биссектрисасы екенін дәлелдейік
жоспар
Қосымша салу.
∆ АСВ және ∆ АDB үшбұрыштарының
теңдігін дәлелдейік.
3. Қорытынды
А
В
С
D
АС=АD, бірдей шеңберлердің радиустары.
СВ=DB, бірдей шеңберлердің радиустары.
АВ - ортақ қабырға.
∆АСВ = ∆ АDВ, үшбұрыштыр теңдігінің III белгісі бойынша
АВ сәулесі - биссектриса
В
А
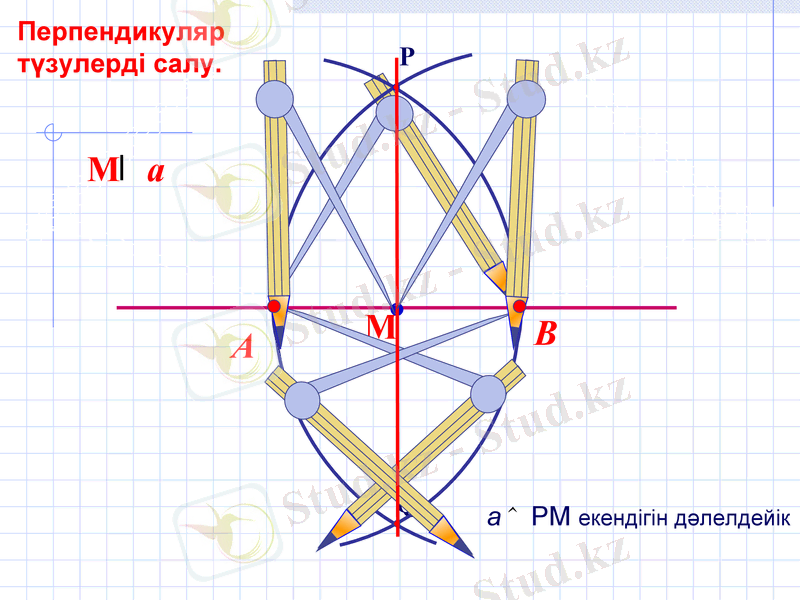
Перпендикуляр
түзулерді салу.
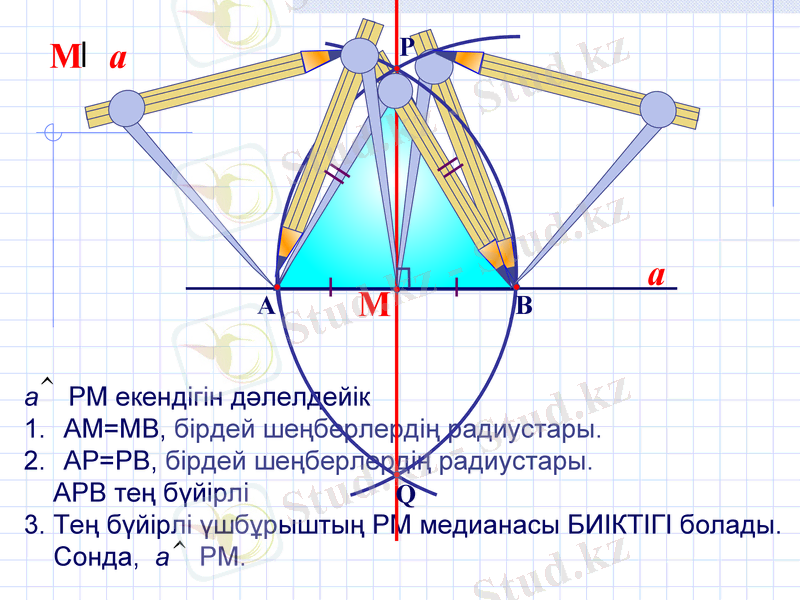
а РМ екендігін дәлелдейік
АМ=МВ, бірдей шеңберлердің радиустары.
АР=РВ, бірдей шеңберлердің радиустары.
АРВ тең бүйірлі
3. Тең бүйірлі үшбұрыштың РМ медианасы БИІКТІГІ болады.
Сонда, а РМ.
М
a
a
N
М
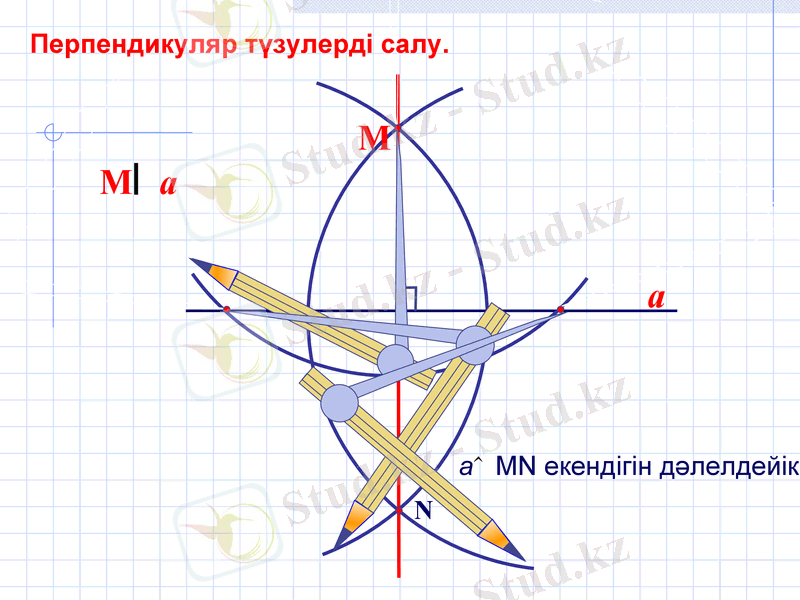
Перпендикуляр түзулерді салу.
a
N
B
A
C
М
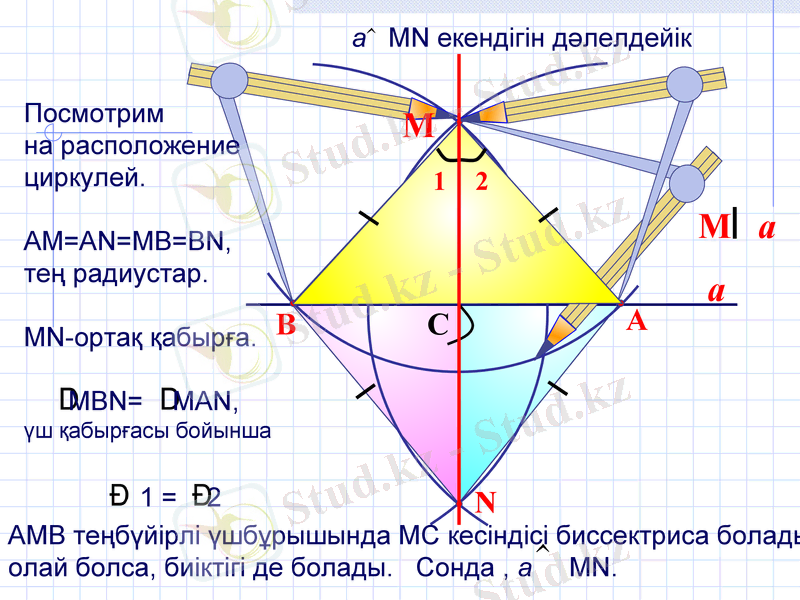
Посмотрим
на расположение
циркулей.
АМ=АN=MB=BN,
тең радиустар.
МN-ортақ қабырға.
MВN= MAN,
үш қабырғасы бойынша
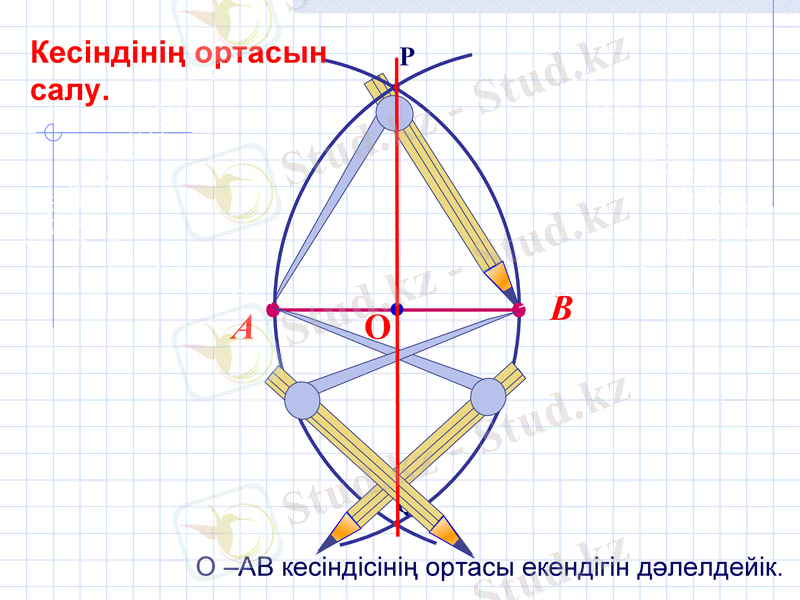
О -АВ кесіндісінің ортасы екендігін дәлелдейік.
Кесіндінің ортасын
салу.
В
А
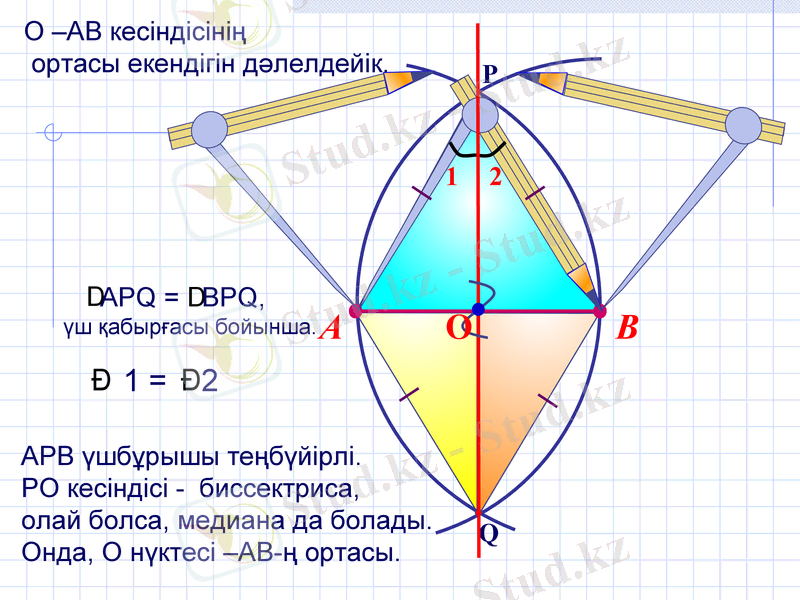
АРВ үшбұрышы теңбүйірлі.
РО кесіндісі - биссектриса,
олай болса, медиана да болады.
Онда, О нүктесі -АВ-ң ортасы.
О -АВ кесіндісінің
ортасы екендігін дәлелдейік.
D
С
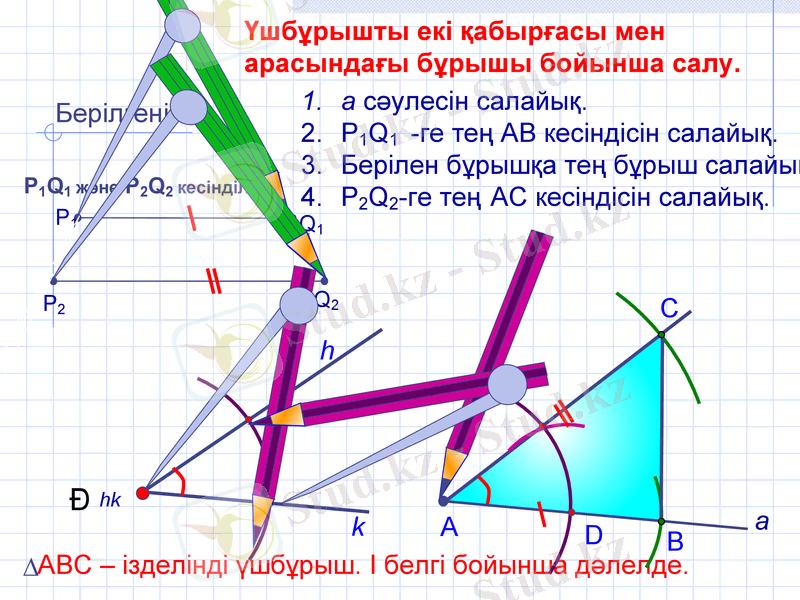
Үшбұрышты екі қабырғасы мен арасындағы бұрышы бойынша салу.
hk
h
а сәулесін салайық.
P1Q1 -ге тең АВ кесіндісін салайық.
Берілен бұрышқа тең бұрыш салайық
P2Q2-ге тең АС кесіндісін салайық.
В
А
АВС - ізделінді үшбұрыш. I белгі бойынша дәлелде.
Берілгені:
Р1Q1 және Р2Q2 кесінділері
Q1
P1
P2
Q2
а
k
∆
D
С
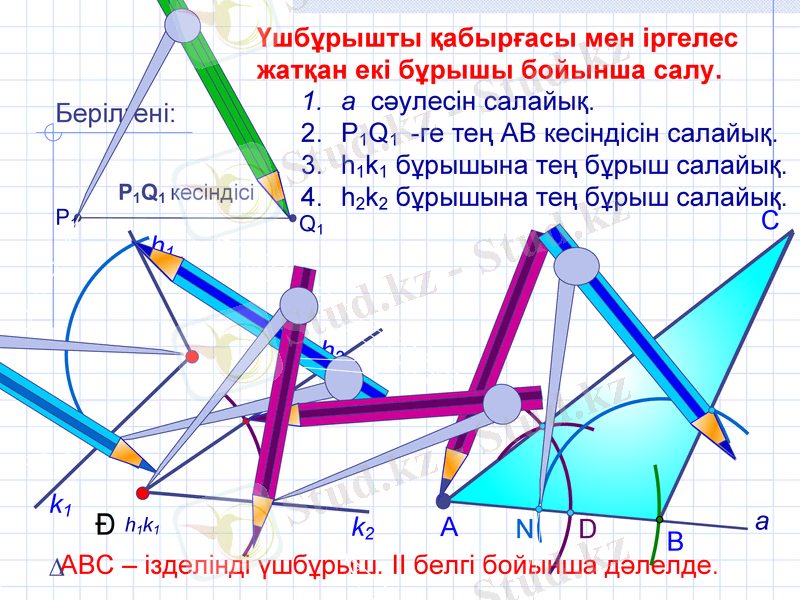
Үшбұрышты қабырғасы мен іргелес жатқан екі бұрышы бойынша салу.
h1k1
h2
а сәулесін салайық.
P1Q1 -ге тең АВ кесіндісін салайық.
h1k1 бұрышына тең бұрыш салайық.
h2k2 бұрышына тең бұрыш салайық.
В
А
АВС - ізделінді үшбұрыш. IІ белгі бойынша дәлелде.
Берілгені:
Р1Q1 кесіндісі
Q1
P1
а
k2
h1
k1
N
∆
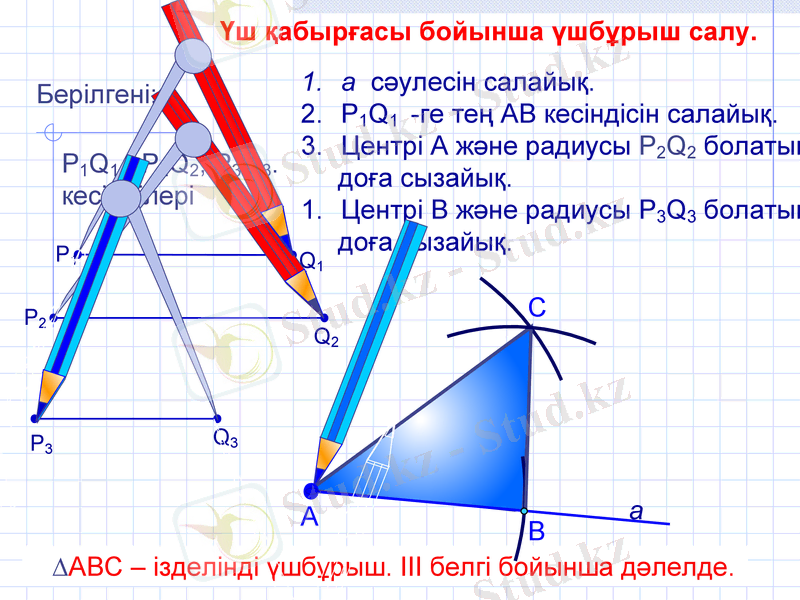
С
а сәулесін салайық.
P1Q1 -ге тең АВ кесіндісін салайық.
Центрі А және радиусы Р2Q2 болатын
доға сызайық.
Центрі В және радиусы P3Q3 болатын
доға сызайық.
В
А
∆АВС - ізделінді үшбұрыш. IІІ белгі бойынша дәлелде.
Берілгені:
Р1Q1, Р2Q2, P3Q3.
кесінділері
Q1
P1
P3
Q2
а
P2
Q3
Үш қабырғасы бойынша үшбұрыш салу.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz