Шұбарқұдық гимназиясы

Функцияның графигіне

жүргізілген жанаманың теңдеуі

Сарин Т. Б.

Үй тапсырмасы:

№192, 193, 194

Өткенге шолу

2) Туындының қандай мағынасы бар?

3) Туындының физикалық мағынасы қандай?

4) Жылдамдықтан алынған туынды неге тең?

5) sʹ(t) =v(t), мұндағы v(t) дегеніміз не?

y=f(х) функциясының xₒ нүктесіндегі

туындысы f ʹ(хₒ) осы функция графигінің

(xₒ; f(xₒ) ) нүктесі арқылы өтетін

жанамасының бұрыштық коэфициентіне

тең: f ʹ(хₒ) =tgα=k

Физикалық

Геометриялық

sʹ(t) =v(t) - қозғалысағы

дененің t уақыт мезетіндегі

лездік жылдамдығы

vʹ(t) =g - жылдамдықтан

алынған туынды

удеуге тең

y=f(x) функциясының х нүктесіндегі

f ʹ(x) туындысы х нүктесіндегі

өзгеру жылдамдығын анықтайды

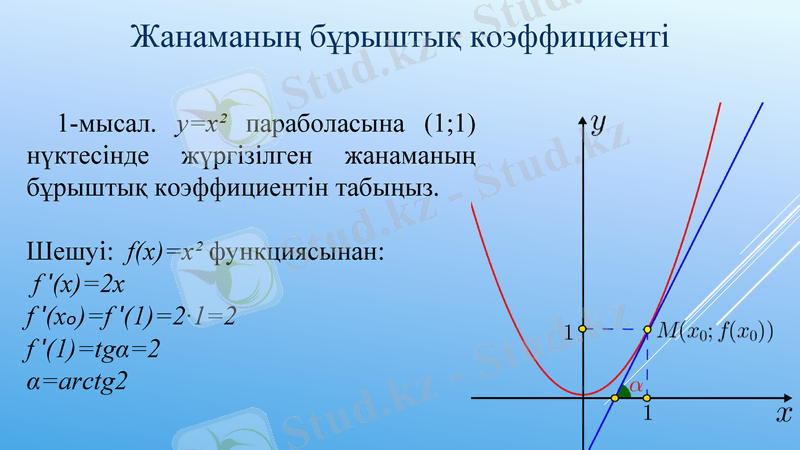
Жанаманың бұрыштық коэффициенті

1-мысал. y=x² параболасына (1; 1) нүктесінде жүргізілген жанаманың бұрыштық коэффициентін табыңыз.

Шешуі: f(x) =x² функциясынан:

f ʹ(x) =2х

f ʹ(xₒ) =f ʹ(1) =2·1=2

f ʹ(1) =tgα=2

α=arctg2

Жанаманың теңдеуі

y=f(x) функциясы Nₒ(xₒ; yₒ) нүктесіндегі f ʹ(xₒ) берілсін. Жанаманың теңдеуі түзу

болғандықтан y=kx+b сызықтық функция ретінде іздейміз.

Мұндағы k=tgα= f ʹ(xₒ), бұдан y= f ʹ(xₒ) x+b.

Nₒ(xₒ; f (xₒ) ) нүктесінің координаталарын қоямыз бұдан f (xₒ) = f ʹ(xₒ) xₒ+b

f (xₒ) = f ʹ(xₒ) xₒ+b теңдеуінен b-ны табамыз: b = f (xₒ) - f ʹ(xₒ) xₒ

b = f (xₒ) - f ʹ(xₒ) xₒ теңдеуін y= f ʹ(xₒ) x+b теңдеуіне қоямыз: y= f ʹ(xₒ) x+ f (xₒ) - f ʹ(xₒ) xₒ

Соңғы теңдеуді ықшамдау арқылы: y= f (xₒ) + f ʹ(xₒ) - (x - xₒ) аламыз.

Бұл жанаманың теңдеуі.

Жанаманың теңдеуін жазу алгоритмі

xₒ -ге сәйкес f (xₒ) -ді есептеу.

f (x) функциясының туындысын табу.

xₒ-дегі туындының мәні f ʹ(xₒ) -ді есептеу.

y= f (xₒ) + f ʹ(xₒ) ·(x - xₒ) формуласына қойып жанаманың теңдеуін алу.

1-мысал:

f (x) =x²-5x+6 функциясының xₒ=1 нүктесіндегі жанаманың теңдеуін жазыңыз.

f (xₒ) =f(1) =1²-5·1+6=2.

f ʹ(x) =2x-5.

f ʹ(xₒ) = f ʹ(1) =2·1-5=-3

y= f (xₒ) + f ʹ(xₒ) ·(x - xₒ) =2-3(x-1) =2-3x+3=5-3x.

Бұдан жанаманың теңдеуі: y=5-3x

Карточкалық тапсырма

f (x) =x²-5x+6 функциясының xₒ=4 нүктесіндегі жанаманың теңдеуін жазыңыз.

f (x) =12-3x+2x² функциясының xₒ=2, 5 нүктесіндегі жанаманың теңдеуін жаз.

f(x) =x²-3x+5 M(0; 5) нүктесі арқылы өтетін жанамасының бұрыштық коэффициентін табыңыз.

b-ның қандай мәнінде y=-10x+b түзуі f(x) =3x²-4x+2 функциясының грaфигіне жанама болады.

b-ның қандай мәнінде y=8x+b түзуі f(x) =x²+2x³ функциясының грaфигіне жанама болады.

Оқулықпен жұмыс

Тест тапсырмасы

Бағалауы:

9-10 өте жақсы.

6-8 жақсы

3-5 қанағаттанарлық

Үйге тапсырма:

№204, №212 есептер

Ұқсас жұмыстар

Гимнастикалық таяқпен жаттығу

Ұрыстық серіппе

Қалыпты күш

Қазақстан Республикасының мұнай өндеу өнеркәсібі экономикасы

Мидың Оқушыларды саралап - бөлімдері

Зерде интеллектуалды сайысы

Мұқағали Мақатаев (1931-1976)

Топ атын

Арал теңізі

Сәнді қолданбалы өнерінің шебер мектебі”

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz