Квадрат теңдеулерді шешу

Квадрат теңдеулер

№15 орта мектеп

8 сынып алгебра сабағы

Шинтимирова Амина Камешқызы №15 орта мектептің математика пәнінінң мұғалімі

Анаграммалар

таиимдкисрнн

кісенді

дуеңте

фэкоцинетиф

бүтір

Ответы:

Квадрат теңдеулерді шешу

Сабақтың тақырыбы:

Сабақтың ұраны:

Мен не істеу керек екенін білемін.

Мен қалай істеу керек екенін білемін.

Сабақтағы эпиграф :

Теңдеулер мен теоремалар

арқасында

Мен бірталай мәселені

шешемін.

(Чосер, орта ғасырлардағы ағылшын ақыны)

Жауабы: - 1; 4 .

Өзіңді тексер

Теңдеу

Толық

Толымсыз

Келтірілген

Келтірілмеген

Жалпы ұпай

Қрьь ате

Қате жоқ - 5 ұпай

1 - 2 қате - 4 ұпай

3 - 4 қате - 3 ұпай

Квадрат теңдеуді шешу алгоритмі

Дискриминант және квадрат теңдеудің түбірлері

D = b2-4ac

D>0

Теңдеудің әр түрлі нақты екі түбірі болады

Виет теоремасы

Салдар

Толымсыз квадрат теңдеулерді шешу

Теңдеудің ең үлкен түбірін табыңдар

Жауабы: 1.

Оқулықпен жұмыс

І нұсқа. Толымсыз квадрат теңдеулерді шешу: №361 (1, 3)

ІІ нұсқа. Келтірілген квадрат теңдеуді шешу: №364 (1, 3)

ІІІ нұсқа. Рационал теңдеуді шешу. №365 (1)

ІҮ нұсқа. Квадрат теңдеуді шешу. №366 (1)

Өзіңді тексер

а)

ә)

1-4 топ

2-5 топ

б)

в)

Түбірі жоқ

1; 1, 5

-1; 1, 5

-1; 3

1; 0, 6

1; -3

-1; -2

-5; -2

-0, 6; 1

3-6 топ

г)

д)

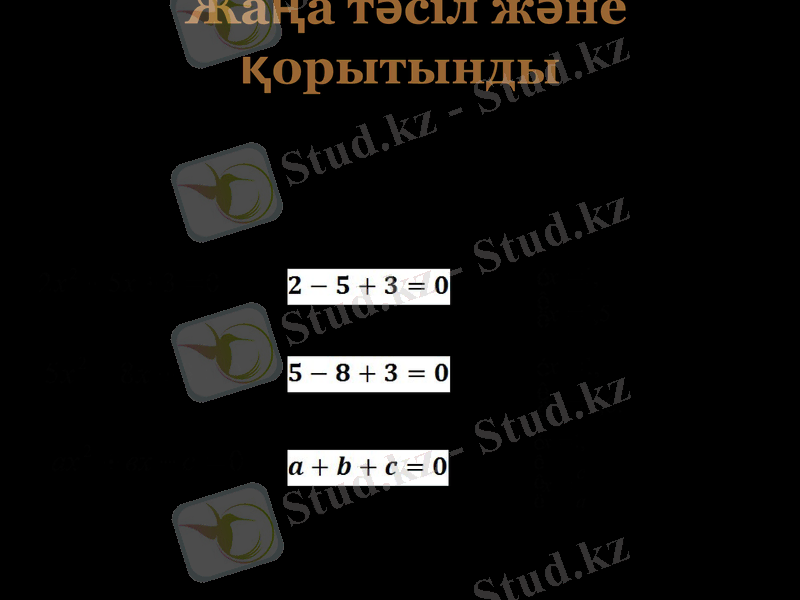
Жаңа тәсіл және қорытынды

Теңдеулер

Коэффициенттері қосындысы

а + в + с

Түбірлері

Жаңа тәсіл және қорытынды

Теңдеулер

а - в + с

Түбірлері

Ауызша есептеңдер:

Аздап тарихқа үңілейік

Квадрат теңдеулер Индияда

«Кім де кім өткенді білмей, қазіргімен ғана шектеліп қалғысы келсе, ол оны ешуақытта түсінбейді»

Лейбниц

Маймылдың бір топ баласы

Тойып алып тамаққа

Секіруін қоймады.

Сегізден бірінің квадраты

Көгалда аунап ойнады.

Он екісі құтырып,

Шырмауыққа асылды.

Барлығы неше хайуан,

Санап көрші, кәнеки,

Болсаң егер ақылды?

БХАСКАР ЕСЕБІ

Шешімі:

Үйге тапсырма:

Шешудің барлық әдістеріне квадрат теңдеулер құрастырып келу

“Квадрат теңдеулер” тақырыбына оқу моделін құрастырып келу.

Бағалау мөлшері

51 - 60 ұпай “5”

45 - 50 ұпай “4”

30 - 44 ұпай “3”

ТОСЫН СЫЙ

теңдеуінің бір түбірі 3-ке тең. Егер р-нің мәнін тапсаңдар, онда партаның нөмірін білесіңдер, ал екінші түбірі тосын сый жатқан партаның қай қатарда екенін көрсетеді.