Квадрат теңдеу түбірлерінің формулалары

Презентация қосу

Тақырыбы:
«Квадрат теңдеу түбірлерінің
формулалары»

Возвышенка орта мектебі
Математика пән мұғалімі
Кожагулова Айшолпан Әлібекқызы
Бар ізгілік тек
білімнен алынар,
Білімменен аспанға
жол салынар.

Жүсіп Баласағұни
04/13/2019 2
ax2 + bx + c = 0 теңдеуін
коэффициенттерінің қасиеттері

Егер a + b + c = 0, онда x1 = 1, x2 =
Егер a – b + c = 0 немесе
b = a + c, онда x1 = -1, x2 = -
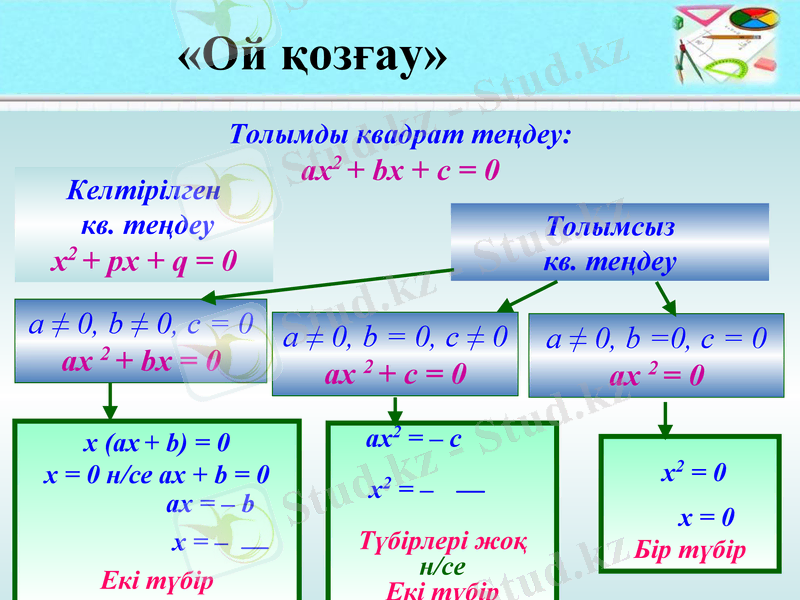
«Ой қозғау»
Толымды квадрат теңдеу:
ах2 + bx + c = 0
Келтірілген
кв. теңдеу Толымсыз
х2 + px + q = 0 кв. теңдеу

a ≠ 0, b ≠ 0, c = 0 a ≠ 0, b = 0, c ≠ 0 a ≠ 0, b =0, c = 0
ах 2 + bx = 0 ах 2 + c = 0 ах 2 = 0

x (ах + b) = 0 ах2 = – c
х = 0 н/се ах + b = 0 с х2 = 0
ах = – b x =–

b a x=0
x=– Түбірлері жоқ
a н/се Бір түбір
Екі түбір
- квадрат теңдеудің
D b 4ac
дискриминанты

3 жағдай болуы мүмкін:

D 0 - түбірлері жоқ

D 0 - бір түбір х= -
D 0 - екі түбір
Берілген теңдеулердің арасынан толық және
толымсыз квадрат теңдеулерді атаңдар

а) х2 + 3х – 19 =0, б) х2-7х+11=0,
ә) 4х2+5х=0, д) 2х2-5х+1=0,
в) 8х2=0, г) 3х2-21х=0.
ғ) 8х2-3х=0, е) х2-25=0,
ж) х2-4х=45 з) 18-2х2=0
и) 4х2-28х+49=0 к) 2х2-5х+3=0
Кестені толтыр!
Квадраттық a b c Түбірлер
теңдеу саны
-3x2+х-2=0

-x2+ 7x + 18
=0

5х2-8х+3=0
Теңдеулерді шешіңдер:

жауабы
X2 + 12x + 20 =0

Теңдеулерді
-X - 6x - 73 =0
2 шешіңдер:
x2+ 2x + 1 =0
• Түбірлері бар бірнеше келтірілген квадраттық
теңдеудің түбірлерін, түбірлерінің қосындысы
мен көбейтіндісінің мәндерін табыңдар және
жауаптарын кестеге толтырыңдар.
Теңдеулер Түбірлер х1+ х2 х1 · х2
х1 және х2
х2 – 2х – 3 = 0
Х2 + 5х – 6 = 0
х2– х – 12 = 0
х2+ 7х + 12 = 0
Бұл мысалдардан, келтірілген квадраттық теңдеу
түбірлерінің қосындысы қарсы таңбасымен
алынған екінші коэффициентке, ал көбейтіндісі бос
мүшеге тең екенін байқадық.
Енді бұл қасиетті теорема ретінде тұжырымдап
шығайық.
Теорема : Келтірілген квадраттық теңдеу
түбірлерінің қосындысы қарсы таңбасымен
алынған екінші коэффициентке, ал көбейтіндісі
бос мүшеге тең болады:
х1 х2 p; x1 x2 q
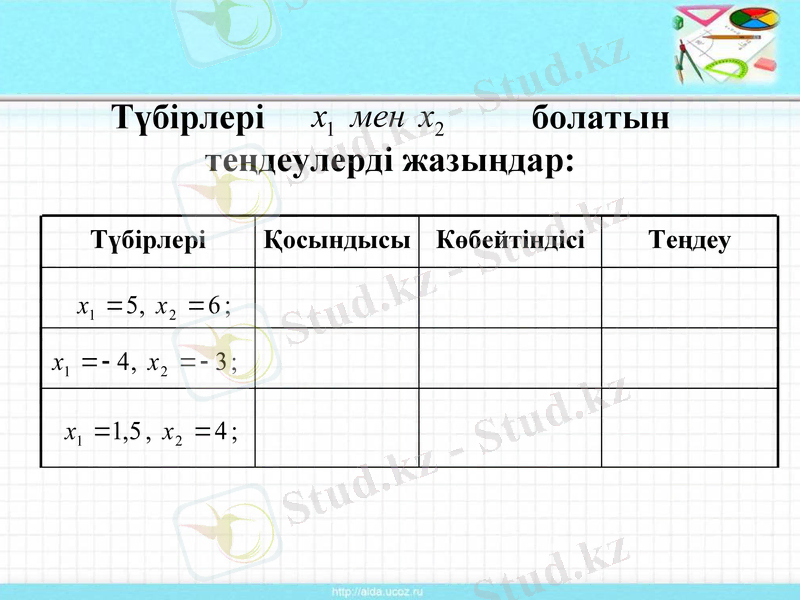
Түбірлері х1 мен х2 болатын
теңдеулерді жазыңдар:

Түбірлері Қосындысы Көбейтіндісі Теңдеу

х1 5, х2 6 ;

х1 4, х2 3 ;

х1 1,5 , х2 4 ;
Тест тапсырмалары
1-нұсқа
1. Квадрат теңдеудің коэффициенттерін жазыңдар:
А) а=5; в=-9; с=4 Б) а=4; в=-9; с=5 В) а=-9; в=5; с=4
2. Теңдеудің түбірін табыңдар:
А) Б) B)
3. Мына теңдеу квадрат теңдеу бола ма?
А) иә Б) жоқ
4. Теңдеуді шешіңдер:
А) -1; 0. В) Түбірлері жоқ. С) 1. D) -1. Е) 0.
5. Келтірілген квадрат теңдеуді көрсет:
А)9
2-нұсқа
1. Квадрат теңдеудің коэффициенттерін жазыңдар:
А) а=-9; b=3; c=1 Б) а=1; b=3; c=-9 В)a=-9; b=1; c=3
2. Теңдеудің түбірлерін табыңдар:
А) Б) C)
3. Мына теңдеу квадрат теңдеу бола ма? 1-12х=0
А) иә Б) жоқ
4. Теңдеуді шешіңдер: 2
А) 1. В) -1; 0.
2-1;
х С) х 11. 0 D) -1. Е) 0.
5. Келтірілген квадрат теңдеуді көрсет:
А) 2
Жауаптарыңызды тексеріңіздер:
1-нұсқа 2-нұсқа
1) А Б
2) Б А
3) Б Б
4) В А
5) С Б

Ұқсас жұмыстар

Толық квадрат теңдеулерді шешу формулалары

Келтіру формуласы

Квадрат теңдеулерді шешу тәсілдері

Оқушы білімін тексеру

Теңдеуді шеш

Сабақтың мақсаттары

Таләйлі болсын талғамың

Виет теоремасы туралы ақпарат

Квадарат теңдеу тарауын қорытындылау

Теңдеудің түбірлерін табыңдар

Пәндер