Кванттық механикадағы физикалық шамалардың операторлары: сызықтылық пен эрмиттілік

Физикалық шамалардың операторлары. Операторлардың сызықтылығы және эрмиттілігі

Тобы: ТФ - 619

Орындаған: Саналбай Ж. Қ.

Жоспар

Кіріспе

Операторлар

Өзіндік функциялар

Эрмиттік оператор

Қорытынды

Кіріспе

Кванттық механика қазіргі заманғы физиканың негізгі теориясының бірі. Кванттық механика - микробөлшектердің (элементар бөлшектердің, атомдардың, молекулалардың) қозғалыс заңдылықтарын зерттейтін теория.

Кванттық механиканы әрі қарай қарастыру үшін, негізгі физикалық шамалардың операторларын білу қажет.

Оператор - бір толқындық функцияны басқа функцияға ауыстыратын математикалық символ, яғни кез келген әрекет. Операторды бүркеншігі бар әріппен белгілейді. Мысалы:

Бұл теңдіктегі оператор ретінде арифметикалық, дифференциалдық және т. б. операторларды қарастыруға болады.

Кванттық механикада пайдаланылатын операторлардың тобы шектелген, себебі, кванттық механика суперпозиция принципіне негізделген. Бұл принципті бұзбас үшін, операторлар сызықтық түрде болу керек. Сызықтық операторлардың математикалық анықтамасын келтіруге болады:

мұндағы с1, с2, - тұрақты сандар.

Операторлар

Физикалық шамалардың операторлары сызықтық ғана емес, өзіне түйіндес болу керек.

Бұл операторлық қатыстағы F тұрақты шама, оның кейбір мәндері 1-ші формуланы қанағаттандырады, олар оператордың өзіндік мәндері деп аталынады. Өзіндік мәндерге сәйкес келетін толқындық функциялар өзіндік функциялар деп аталынады. Кванттық механикада өзіндік мәндер әрқашан бақыланатын физикалық шамалар болып табылады. Ал, бақыланатын физикалық шамалар нақты сандар болу керек, яғни F=F* . Мұндағы F*-F шаманың түйіндес мәні. Өзіндік мәндердің нақты шамалар болу шарты, операторлардың өзіне түйіндес болуына келтіреді. Өзіндік функция Ψ және оның түйіндесі Ψ*-ге арналған екі қатысты жазайық:

Өзіндік функциялар

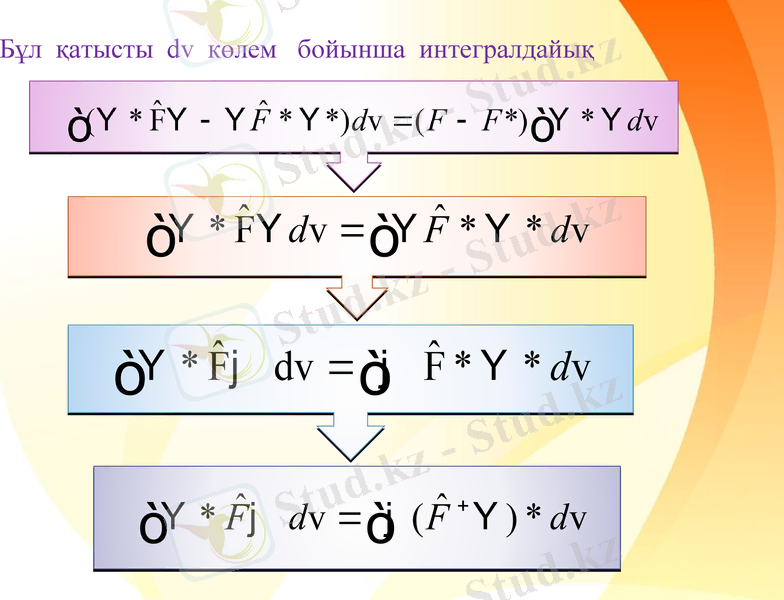
Бұл қатысты dv көлем бойынша интегралдайық

Соңғы екі формуланы салыстыра отырып, операторлардың өзіне түйіндес болу шартын қысқаша түрде көрсетейік:

мұндағы «+» символын эрмиттік түйіндес амалы ретінде түсіну керек. - эрмиттік оператор деп аталынады.

Енді бастапқы операторға қатысты аударылған операторын анықтайық:

мұндағы ~ (тильда) белгісі φ және Ψ* функцияларының орын ауыстырғанын көрсетеді.

Эрмиттік оператор

Қорытынды

Қорытындылай келе, оператор дегеніміз - бір толқындық функцияны басқа функцияға ауыстыратын математикалық символ, яғни кез келген әрекет. Өзіндік мәндерге сәйкес келетін толқындық функциялар өзіндік функциялар деп аталынады.