БЕТТІҢ АНЫҚТАМАСЫ

Скачать

Дифференциалдық геометрияның беттер теориясы, есептері

Кіріспе

Менің курстық жұмысымның тақырыбы «дифференциалдық геометрияның беттер теориясы, есептері».

Беттер теориясы - дифференциалдық геометрияның беттерінің қасиетін зерттейтін саласы. Классикалық беттер теориясында беттің қозғалыс кезінде өзгермейтін қасиеттері қарастырылады. Оның негізгі есептерінің бірі - беттегі өлшеулер. Беттегі өлшеулердің көмегімен алынған фактілер жиынтығы беттің ішкі геометриясын құрайды. Сызықтың ұзындығы, екі бағыттың арасындағы бұрыш, сондай-ақ, геодезиялық сызық, геодезиялық сызықтың қисықтығы, т. Б. Ұғымдар беттің ішкі геометриясының ұғымдарына жатады.

Жалпы жағдайда беттің табиғаты сан алуан болып келеді. Сондықтан оны жазықтықтың бөлігінен деформация арқылы алу мүмкін емес. Олар өзін-өзі қиятын немесе беттескен бөліктері де бар болуы мүмкін. Дегенмен, мұндай беттің әрбір нүктесінің маңайының құрылымы элементарлық бет тәрізді болып келеді.

Беттердің геометриялық қасиеттерін зерттеу үшін оларға кейбір шарттар - регулярлық шартын қоямыз. Ерекшеліктері жоқ беттерді қарастыруымен ғана шектеліп қоймай және оларды зерттеу үшін тиімді тәсілдерді дамытып, біз беттердің кейбір маңызды сипаттамаларын: бетке жүргізілген жанама жазықытық және нормаль, бірінші және екінші квадраттық формалар және т. б. енгіземіз.

Беттің анықтамасы

Жанама жазықтықтың анықтамасы

Беттің нормалі

Беттің бірінші квадраттық формасы

Беттің екінші квадраттық формасы

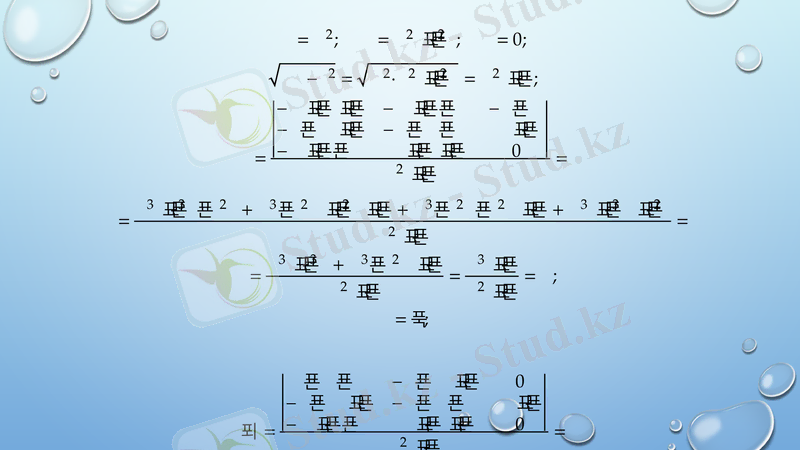
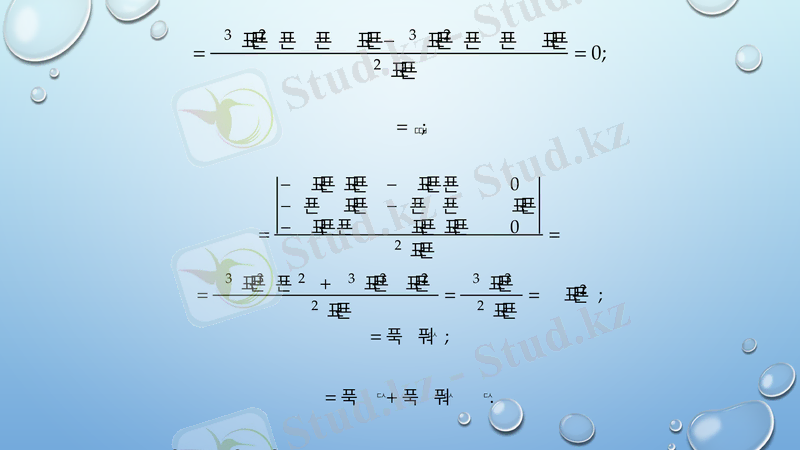
Қорытынды

Менің бұл курстық жұмыста қамтыған мәселелерім: бет туралы ұғым, бетке жүргізілген жанама жазықтық және нормаль, беттің бірінші квадраттық формасы, беттің екінші квадраттық формасы және осы қарастырған тақырыптарыма арналған есептер.

Есеп мағынасын білу үшін, әрине, оның шығару жолын түсініп алуымыз міндетті. Сондықтан да беттер теориясын көп ізденіп есептерге тоқталдым.

Дифференциалдық геометрияның беттер теориясын іздестіру барысы маған аса қиындық тудырған жоқ. Беттер теориясының бастапқы ұғымын А. Т. Мусин, Ж. Нұрпейісов, А. В. Погорелов және т. Б кітаптарынан талдай отырып жаздым.

Ізденістер барысында «беттің бірінші және екінші квадраттық формасы» жақсы ашылған кітап - н. Хайруллина (дифференциалдық гоеметрия) екендігін байқадым.

Мен бұл курстық жұмысты жаза отырып беттер теориясын толық білдім және оны шығару түрлерін зерттедім, іздендім және білімімді одан әрі шыңдадым. Теориялық материалды жақсы біліп қана қоймай, оны есептер шығаруда тиімді пайдалана білу қажет. Беттер теориясын есептеудің бірнеше түрлерімен және көптеген шығару тәсілдерімен таныстым. Енгізген формулалардың әрқайсысына тоқталып кеттім.

Қорыта келгенде, жеке жұмыс жазғанда ең бастысы талпыныс болу керек. Менің зерттеген тақырыбым қызықтырарлық болды. Өз алдыма қойған сұрақтарға жауап беріп, қойған мақсатыма жеттім деп айта аламын.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс