Анықталған интеграл және оның қолданылулары

Презентация қосу

Анықталған интеграл
және оның қолданылулары
Кіріспе
Менің курстық жұмысымның тақырыбы «Анықталған интеграл және оның қолданылулары».
Интеграл (лат. іnteger – бүтін) – 1. математиканың маңызды ұғымдарының бірі. Интеграл ұғымы бір
жағынан – туындысы бойынша функцияны іздеу (мысалы, қозғалған нүктенің жүріп өткен жолын
өрнектейтін функцияны сол нүктенің жылдамдығы бойынша табу), екінші жағынан – аудан, көлем
және доға ұзындығын өлшеу, күштің белгілі бір уақыт ішінде атқарған жұмысын табу, т.б.
қажеттіліктерден пайда болды. Осыған қатысты интеграл анықталмаған интеграл және анықталған
интеграл болып ажыратылады. Міне, осыларды есептеу интегралдық есептеудің міндеті болып
саналады. «Интеграл» сөзін алғаш рет (1690) швейцариялық ғалым Якоб Бернулли қолданған; 2.
өзінің шексіз аз бөліктерінің қосындысы түрінде қарастырылатын бүтін шама.
Зерттеудің мақсаты: анықталған интеграл және олардың қолданылу жолдарын талдау.
Зерттеудің міндеті: анықталған интегралды интегралдаудағы теориялық бөлімін қарастыру.
Анықталған интегралды интегралдауды есептер мен мысалдарда қарастыру.
Зерттеу әдістері: талдау нәтижесінде алынған мәліметтерді бақылап, тақырып бойынша
әдебиеттерді зерттеу.
Құрылымы: курстық жұмыс кіріспеден, негізгі бөлімнен, практикалық бөлім, қорытынды және
қолданылған әдебиеттер тізімінен тұрады.
Анықталмаған интеграл

Бізге функцияның туындысы белгілі, енді осы функциясының өзін табу керек.
Анықтама. Егер аралығындағы үшін

теңдігі орындалса, онда осы аралықта функцияны функцияның алғашқы функциясы
деп атайды.
Анықтама. интервалындағы функцияның алғашқы функцияларының жиынын
функцияның анықталмаған интегралы деп атайды да, символымен белгілейді.
Мұндағы интеграл астындағы функция, , интеграл астындағы өрнек деп аталады.
Сонымен анықтама бойынша
Анықталған интеграл

[a,b] кесінді де функциясы анықталсын. нүктелер арқылы [a, b] кесіндіні n дербес бөліктерге бөлеміз.
Дербес бөліктердің ең үлкенінің ұзындығын деп белгілейміз, мұндағы Әрбір дербес кесіндіден кез келген
нүктені таңдап алып, осы нүктедегі функцияның мәнін деп белгілеп мынадай қосындыны құрайық

(1.1) қосынды Риманның интегралдық қосындысы деп аталады. Енді осы (1.1) интегралдық қосындының
ұмтылғандағы шегін қарастырайық

Анықтама. Егер (1.2) қосындының шегі ұмтылғанда бар болса және ол шек [a, b] кесіндіні қалай
бөлшектегенге және нүктелерін қалай таңдап алғанға байланысты болмаса, онда ол шек функцияның [a, b]
кесіндідегі анықталған интегралы деп аталады да, мына таңбалықпен белгіленеді

Кейде (1.3) функцияның [a, b] кесіндідегі Риман интегралы деп те аталады. a және b сандары интегралдың
сәйкес төменгі және жоғарғы шектері, – интеграл астындағы функция, – интеграл астындағы өрнек , х –
интегралдау айнымалысы, [a, b] - интегралдау аймағы (облысы) деп аталады.
Анықталған интегралдарды есептеу әдістері
Айнымалыны ауыстыру
Ескерте кететін бір жағдай: интегралдау айнымалысын басқа бір тәуелсіз
айнымалысымен ауыстырғаннан анықталған интеграл өзгермей қалады:

Теорема. Айталық, функциясы [a, b] сегментінде үздіксіз болсын. Ал, функциясының
сегментінде үздіксіз туындысы бар болсын және де мен теңдіктері орындалсын.

Сонда:
Бөліктеп интегралдау

Енді және функциялары аралығында дтфференцталданатын болса, онда,

Бұл формуланы анықталған интегралды бөліктеп интегралдау формуласы деп атайды. Енді
(1) формуланы дәлелдейік:
Ньютон-Лейбниц формуласы бойынша:

Бұдан ізделінді формуласы шығады:
Анықталған интегралдың қолданылуы
Жазық фигура ауданы

1) Егер болса, онда x = a, x = b түзулермен және Ох осімен, қисығымен
шенелген қисықсызықты трапецияның ауданы (77-сурет) мына анықталған
интеграл арқылы есептеләнеді:

2) Егер болса, онда 78-суреттегі қисықсызықты трапецияның ауданы
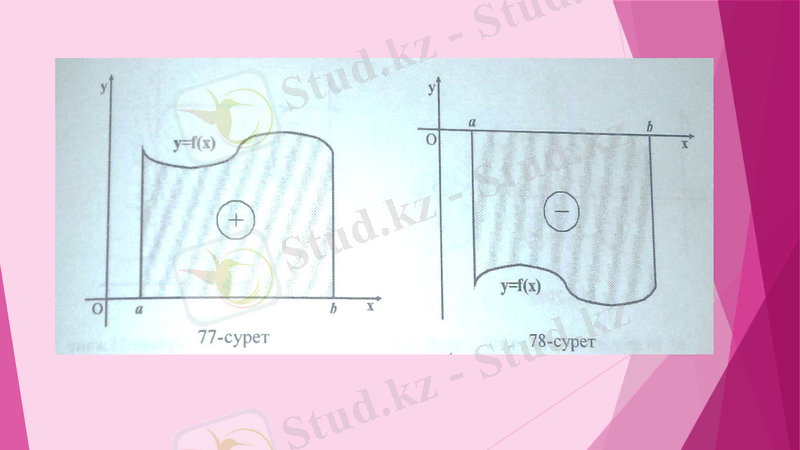
Жазықтықтағы доғаның ұзындығы
1) Жазықтықтағы декарт координат жүйесінде қисығы берілсін (89-сурет).

түзулермен шектелген АВ доғаның ұзындығын табу керек. Абсциссалары болатын АВ доғаның
нүктелерінен хордаларын жүргіземіз, олардың ұзындығын деп белгілейміз. Онда АВ доғаның
орнына іштей сызылған сынығын аламыз. Бұл сынықтың ұындығы

тең. Онда АВ доғаның ұзындығы
2) Егер қисықтың теңдеуі параметрлі түрде берілсе , мұндағы және функциялары және олардың
туындылары кесінді де үзіліссіз болса, онда қисықтың ұзындығын мына формуламен табамыз

Бұл формула (13) теңдеуге және қойғаннан шығады.

Мысал 1: шеңбердің ұзындығын табыңдар.

Шешімі: АВ доғаның теңдеуі . Осыдан

3) Полярлық координат жүйесінде берілген доғаның ұзындығы. Полярлық
координаттағы АВ қисықтың теңдеуі

болсын. Полярлық координаттар мен декарт координаттар арасындағы байланыс
мынаған тең

(15) теңдеуді (16)-ға қойып.

теңдіктерін аламыз. Бұл теңдеулерді қисық доғаның параметрлі түрдегі теңдеулері деп
қарастырып (14) формуланы қолдануға болады.

Онда

Сондықтан

Мысал 1: кардиоидтың ұзындығын табу керек.

Шешімі: кардиоидтың ұзындығын табу үшін (18) формуланы пайдаланымыз
Параллель қималардың ауданы арқылы көлемді есептеу

Бізге дене берілсін (91-сурет). Осы Ох осьіне перпендикуляр әрбір қимасының ауданы белгілі болсын. Осы дененің табу керек.
Денені жазықтармен бірнеше бөліктерге бөлейік. Әрбір бөліктен нүктені таңдап алайық та, әрбір -дің мәніне цилиндр
тұрғызайық. Бұл цилиндрдің жасаушысы Ох осьіне параллель, ал оның бағыттаушысы жазықтықтың денедегі қимасы.
Табанының ауданы -ге тең элементарлы цилиндрдің көлемі -ге тең. Ал барлық цилиндрдің көлемі

ұмтылдырып, дененің көлемінн табамыз.

Сонымен дененің көлемі

формуламен табылады.
Айналу дененің көлемі
қисықпен Ох осьмен, және түзулермен шенелген қисықсызықты трапеция Ох осьмен айналғанда
шыққан денені қарастырайық (92-сурет). Бұл дененің Ох осьне перпендикуляр жазықтықпен
қиғандағы қимасы дөңгелек болады. Ол қиманың ауданы

(20) формуланы қолданып

Егер қисықсызықты трапеция функциямен және түзулермен, Оу осьмен шенелсе, онда бұл
трапецияның Оу осьмен айналғанда шыққан дененің көлемі мына формуламен есептелінеді:

Мысал 1:

сызықтармен шенелген қисықсызықты трапеция Ох осьмен айналғанда шыққан
дененің көлемін табу керек.

Шешімі:
Қорытынды
Менің бұл курстық жұмыста қамтыған мәселелерім: анықталмаған интеграл, анықталған интеграл,
анықталған интегралды есептеу әдістері және оның қолданылулары.
Есеп мағынасын білу үшін, әрине, оның шығару жолын түсініп алуымыз міндетті. Сондықтан да
анықталған интегралдың физикалық анықтауларда маңызды орын алатынын ескере отырып, оларға
да қысқаша тоқталдым. Интегралдар квадратталатын фигуралардан оңтайлы жолмен мән табудың
тамаша тәсілі. Анықталған интегралдың қасиеттерін О.А.Жаутіков, Е.Ә.Қасымов, Тоқбергенов Ж.Б.
т.б кітаптарынан талдай отырып жаздым. Ізденістер барысында анықталған интегралдың физикалық
мағынасы жақсы ашылған кітаптар – Қ.Үсенбаева (Жоғары математика курсы) екендігін байқадым.
Мен бұл курстық жұмысты жаза отырып анықталған интегралдарды есептеуді және оны шығару
тәсілдерін зерттедім, іздендім және білімімді одан әрі шыңдадым. Теориялық материалды жақсы
біліп қана қоймай, оны есептер шығаруда тиімді пайдалана білу қажет. Анықталған интегралдарды
есептеудің бірнеше түрлерімен және көптеген шығару тәсілдерімен таныстым. Әрбір оқулықтағы кез
келген есепті шығаруға болады. Ең бастысы оны есептеудің бір әдісін табу керек. Енгізген
формулалардың әрқайсысына тоқталып кеттім. Бұл тақырып өте қызықты және өзіме түсінікті
болды.
Қорыта келе интегралдардың біздің өмірімізде маңызы зор екендігін байқадым. Және де оны үйрену
барысында математиканың физикаға қажеттілігін тереңінен ұғындым.
Назарларыңызға
Назарларыңызға
рахмет!
рахмет!

Ұқсас жұмыстар

Қос интеграл

Меншіксіз интегралдар

Интегралдық есептеу термині мен интеграл таңбасы Лейбництен бастап қолданылып

Анықталған интеграл. Анықталған интегралдың бар болу шарты. Анықталған интегралдың негізгі қасиеттері. Орта мән туралы теорема. Ньютон-Лейбнец формуласы. Анықталған интегралды интегралдау әдістері. Анықталған интегралдың қолданылуы

Анықталмаған интеграл

Алғашқы функция және интеграл

Анықталмаған интеграл қасиеттері

Алғашқы функция және интеграл тарауын қайталап, бекіту

Математика пәнінің мұғалімі

ШЕК ТАБУДЫҢ ӘРТҮРЛІ ТӘСІЛДЕРІ

Пәндер