Қос интеграл

Интегралдар және қолданылулары

Кіріспе

Мен өзімнің курстық жұмысымда «Интегралдар және олардың қолданылуларын» қарастырамын.

Интеграл (лат. integer-бүтін) -математиканың маңызды ұғымдарының бірі. Интеграл ұғымы бір жағынан- туындысы бойынша функцияны іздеу(мысалы, қозғалған нүктенің жүріп өткен жолын өрнектейтін функцияны сол нүктенің жылдамдығы бойынша табу), екінші жағынан - аудан, көлем және доға ұзындығын өлшеу, күштің белгілі бір уақыт ішінде атқарған жұмысын табу, т. б. қажеттіліктерден пайда болды. Осыған қатысты интеграл анықталмаған интеграл және анықталған интеграл болып ажыратылады. “Интеграл” сөзін алғаш рет (1690) швейцариялық ғалым Якоб Бернулли қолданған; өзінің шексіз аз бөліктерінің қосындысы түрінде қарастырылатын бүтін шама.

Интеграл ұғымы көп айнымалысы бар функцияларға да қолданылады. Интегралдық есептеудің аудан мен көлемді табуға байланысты бірқатар есептерін ежелгі грек математиктері шешкен. 9-15 ғғ. Орта және Таяу Шығыс ғалымдары Архимед еңбектерін араб тіліне аударып, ежелгі математиканың табыстарын кейінгі ұрпақтарға жеткізді. Бірақ оларды одан әрі дамыта алмады. Интегралдық есептеудің негізгі ұғымдары мен идеялық жүйесін бір-біріне тәуелсіз түрде Исаак Ньютон мен Готфрид Лейбниц жасады. “Интегралдық есептеу” термині мен интеграл таңбасы Лейбництен бастап қолданылып. Жалпы үш еселі интеграл дененің көлемін есептеу және пайдалану жолдары, физикалық және механикалық қолданулары қарастырылады.

Мақсаты: Интегралдар және оның қолданылуларын толық қарастыру

Міндеті: интегралдармен танысу, есептерін шығаруды үйрену, қолданылуларын ажырата білу.

Анықталмаған интеграл

Негізгі кестесі:

Анықталған интеграл

Анықталған интегралдың қолданылуы Қисық доғасының ұзындығы.

Жазық фигура ауданы.

Егер [а, b] кесіндісінде функция f(x) ≥0 болса, онда анықталған интеграл анықтамасы бойынша y = f(x) қисығымен, Ох-өсімен және х=а, х=b түзулерімен шенелген қисық сызықты трапеция ауданы

S=abfxdx=abydx (3)

тең.

Егер [а, b] -де f(x) ≤0 болса, онда (3) анықталған интегралда ≤0 болады, ал оның абсолют шамасы сәйкес қисық сызықты трапецияның ауданына тең.

Егер f(x) таңбасы [а, b] -де ақырлы сан рет өзгерсе, онда y = f(x), Ох, х=а, х=b қисықтарымен шенелген жазық фигура ауданы үшін [а, b] кeciндiciн f(x) таңбасы тұрақты болатындай бөліктерге бөліп, осы бөліктер бойынша алынған интегралдардың абсолют шамаларының қосындысын алуға болады немесе

S=abf(x) dx (4)

интегралын есептеу керек (29-сурет)

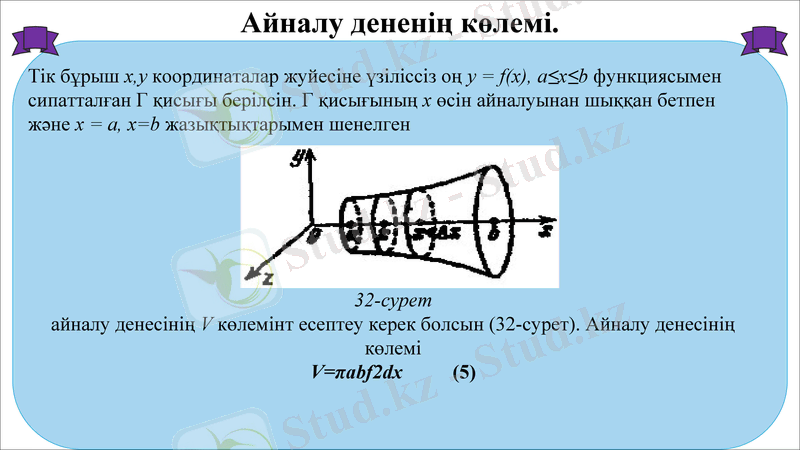
Айналу дененің көлемі.

Тік бұрыш х, y координаталар жуйесіне үзіліссіз оң y = f(x), a≤x≤b функциясымен сипатталған Г қисығы берілсін. Г қисығының х өсін айналуынан шыққан бетпен және х = а, х=b жазықтықтарымен шенелген

32-сурет

айналу денесінің V көлемінт есептеу керек болсын (32-сурет) . Айналу денесінің көлемі

V=πabf2dx (5)

Қос интеграл

Қос интегралдың қолданылулары Жазық фигураның ауданын есептеу

Қос интеграл астындағы екі айнымалының функциясы f(x, y) =1 болса, онда қос интеграл (D) жазық фигурасының ауданын беретінін қос интеграл қасиетінен білеміз. Ал енді (D) облысы

теңсіздіктерімен анықталатын болса, онда аудан

қайталама интеграл бойынша есептелінетін болады.

Ал егер (D) фигурасы поляр координат жүйесінде

теңсіздіктерімен анықталатын болса, онда

Пластинканың массасы

Пластинканың ауырлық центрінің координаттары

Пластинканың инерция моменттері

Үш еселі интеграл

Үш еселі интегралдарда айнымалыны алмастыру

Қорытынды

Менің бұл курстық жұмыста қамтыған мәселелерім: анықталмаған интеграл, анықталған интеграл, қос интеграл, қос интегралдың геометриялық мағыналары, айнымалымен ауыстыру және есептеулері, қос интегралдың геометриялық және физикалық қолданулары, үш еселі интеграл.

Есеп мағынасын білу үшін, әрине, оның шығару жолын түсініп алуымыз міндетті. Сондықтан да қос интегралдың геометриялық және физикалық анықтауларда маңызды орын алатынын ескере отырып, оның есептеу жолдарын, тәсілдерін дәлелдеулер арқылы қысқаша баяндадым.

Интегралдарды қолдана білу өте маңызды. Себебі, техника және технологияның дамуына қос интегралдың үлесі зор. Мысалы: физиканың негіздері болып табылатын масса, ауырлық центрі, инерция және статикалық моменттер қос интегралдық есептеулерді қажет етеді. Ал геометрияда (физикалық байланыстарды ескере отырып) жазық фигураның ауданы, дененің көлемі, бет ауданын есептеуде оңай және тиімді шығару жолымен үлесі зор екендігін білеміз. Сол себептен мен қос интегралдың қолдануларын толыққанды қарастыра алу үшін геометриялық және физикалық (механикалық) деп қолдануларын екіге бөліп қарастырдым. Және де оларды тармақтай отырып, ережелері мен мысалдарын келтірдім. Ізденістер барысында физикалық мағынасы жақсы ашылған кітаптар - А. Т. Мусин, Дүйсек. А. К (қысқаша анықтама), Н. М. Махмеджанов (Жоғары математика есептер жинағы) екендігін байқадым. Әйткенмен бұл кітаптармен тоқталып қалмай тағы да басқа кітаптардан ізденіс жүргіздім.

Қорыта келе интегралдардың біздің өмірімізде маңызы зор екендігін байқадым. Және де оны үйрену барысында математиканың физикаға қажеттілігін тереңінен ұғындым.