Функциялар және олардың қасиеттері: анықтау, берілу тәсілдері және мысалдар

Функциялар және оның қасиеттері

Орындаған:Жанабек Иран

Тобы:МИ-21

Кіріспе

Мен өзімнің курстық жұмысымда функциялар және оның қасиеттері туралы қарастырамын. Функция - математикалық және жалпығылыми ұғымдардың негізгі бөлігі болып табылады. XVII ғасырда функция ұғымының пайда болуына жолды француз ғалымдары Франсуа Виет және Рене Декарт ашты, олар кейін жалпы әлем мойындаған біріңғай математикалық белгілеуді құрастырды. Біріңғай белгілеу ұсынылды: белгісіздерді - латын алфавитінің соңғы әріптерімен - x, y, z; белгілілерді алғашқы әріптермен - a, b, c, . . . және т. с. . Әрбір әріп арқылы тек нақты мәліметтерді ғана емес, басқа да мәліметтерді түсінуге болатын еді. Осылай, математика ғылымына өзгерту идеясы келді.

Сонымен қатар, Декарт пен Фермде (1601-1665) геометриялық еңбектерінде айнымалы шама және тік бұрышты координаталар жүйесі туралы анық түсінік береді. 1637 жылғы «Геометрия» еңбегінде Декарт функция ұғымына түсінік береді, нүкте ординатасының өзгерісін абцисса өзгеруіне тәуелділігін зерттеді. Кейін функция ұғымы анықтала бастады.

Курстық жұмыстың міндеттері:

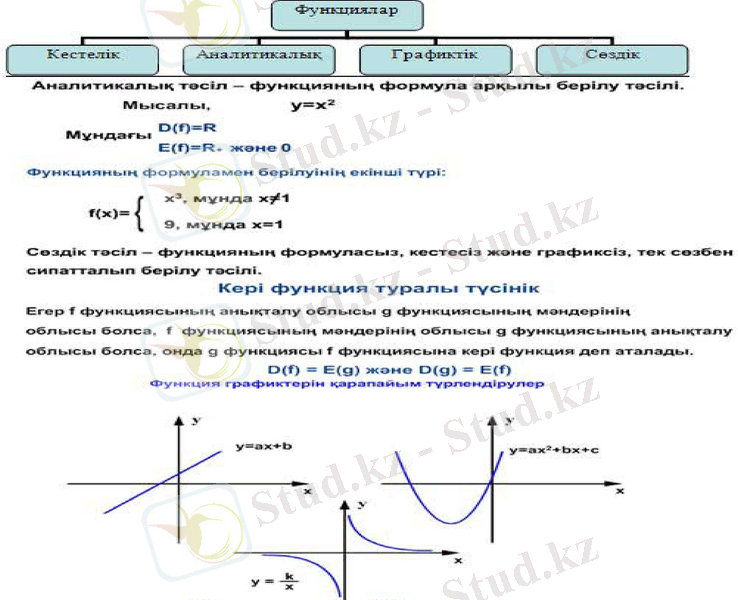
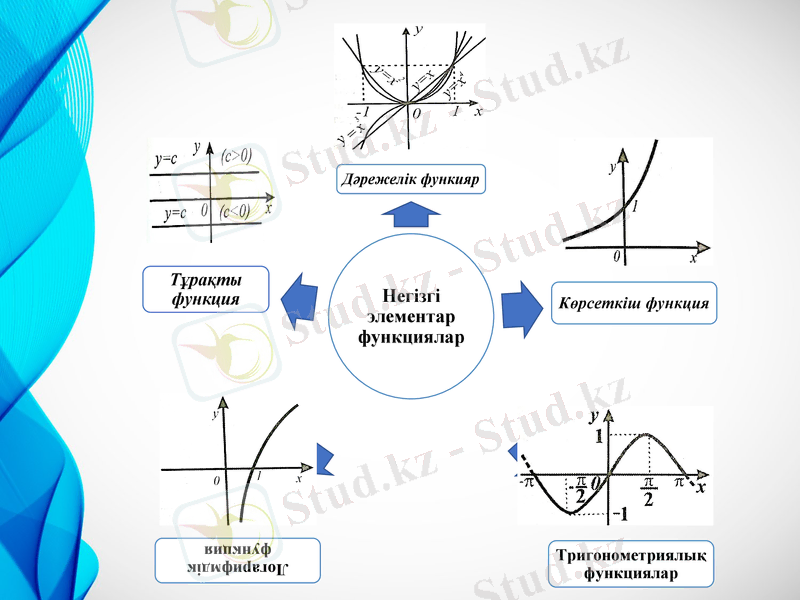
Функцияның қасиеттері

Қорытынды

Менің курстық жұмысымда қарастырған мәселелерім: функцияның негізгі тәсілдері, олардың қасиеттері, негізгі элементар функциялар. Тарихы тереңде жатқанына мән беріп, қазіргі зерттелген деректермен ұштастырдым. Вавилоннан бастау алған функция ұғымының осы уақытқа дейінгі кезеңдеріне шолу жасап, күрделену жолдарына аса мән бердім. Әсіресе, негізгі ұғымдарды О. А. Жаутіков, Қ. Қабдықайыр, Х. И. Ибрашев, Х. Т. Отаровтың еңбектерінен алдым. Бұл кітаптарда функция ұғымына қатысты мәліметтер нақты, әрі түсінікті түрде жазылған. Ал Тоқберген Ж. Б., Е. Ә. Қасымов, Қ. Ә. Қасымов сияқты ғалымдар кітаптарында функция ұғымына қысқаша тоқталған. Дегенмен де осы еңбектердің арқасында үлкен ізденістерге баруға тура келді, бағыт-бағдар берді десем қалт айтпағаным. Н. М. Мұхамеджанов, П. П Коровкин кітаптарынан мысалдар мен есептер ала алдым. Және де 1-курсты қолданған өзімнің есеп дәптерімнің де көмегі тиді. Қорыта келе функция ұғымының қолданылу аясы кең екеніне көзім толықтай жетті. Оның тек сол салада ғана емес, математикалық талдаудың өзге де салаларында қолданылатындығын білдім. Пәнаралық қатынасты ескеретін болсақ бұл ұғымды физикадан да байқауға болады. Осы кезде Н. И. Лобачевскийдің « . . . математиканың шынайы өмірде қолданылмай қалған бірде-бір саласы жоқ . . . » деген сөзінің бекер айтылмағаның да байқадым. Курстық жұмысты жазу барысы үлкен ізденістерді талап етті. Өзіме қызықты болды. Осы еңбегім - сәтті шыққан жұмыстарымның бірі.