ЕКІНШІ РЕТТІ СЫЗЫҚТАР

Курстық жұмыс

Жоспар:

КІРІСПЕ . . .

Екінші ретті сызықтардың жалпы теңдеуі . . .

Екінші ретті сызықтардың жалпы теңдеуін түрлендіру

Жанаманың теңдеуі . . .

Екінші ретті сызықты теңдеудің оптикалық қасиеттері

Есептер . . .

ҚОРЫТЫНДЫ . . .

Пайдаланылған әдебиеттер тізімі . . .

Кіріспе

XIX ғасырдың 80-жылдарында француз математигі К. Жорданның ұсынуы бойынша кез келген шағын аймақтағы байланысқан континуум (мысалы, үшбұрыш, төртбұрыш, куб, т. б. ) кесіндінің үздіксіз бейнесі бола алады. Кесіндінің бірмәнді үздіксіз бейнесін қарапайым доға немесе жордан доғасы деп, ал шеңбердің бірмәнді үздіксіз бейнесін қарапайым тұйық сызық деп атайды. Қазіргі топологияда сызық ұғымының 1921 ж. кеңес математигі П. С. Урысон ұсынған анықтамасы қолданылады. Оның айтуы бойынша сызық - өлшемділігі 1-ге тең еркін алынатын континуум.

Екінші ретті сызықтарды ежелгі заманның математиктері зерттей отырып, бірқатар жоғары ретті алгебралық қисықтарды және транцендент сызықтарды қарастырды. Алайда сызықтарды зерттеу және оларды кластарға бөлу аналитикалық геометрия қалыптасқаннан кейін ғана басталды.

Зерттеудің мақсаттары: Екінші ретті сызықтардың оптикалық қасиеттерін зерттеу.

Міндеттері:

1. Екінші ретті сызықтар туралы мәлімет беру.

2. Екінші ретті сызықтардың оптикалық қасиеттерін қарастыру.

3. Курстық жұмысқа сәйкес есептерді шығару.

Курстық жұмыстың өзектілігі:Аналитикалық геометрия курсында екіншінші ретті қисықтар өзектілігін жоғалтқан емес.

Зерттеудің пәні: Аналитикалық геометрия.

Курстық жұмыстың құрылымы: Курстық жұмыс кіріспеден, үш бөлімнен тұрады. Кіріспеде курстық жұмыстың өзектілігі мен мақсаты көрсетілген. Бірінші бөлімінде екінші ретті сызықтардың қасиеттері қарастырылады. Екінші бөлімінде екінші ретті сызықтардың оптикалық қасиеттері қарастырылған. Қорытынды жасалынды және тақырып бойынша есептер шығарылды.

1. Екінші ретті сызықтардың жалпы теңдеуі

1. 2 Жанаманың теңдеуі

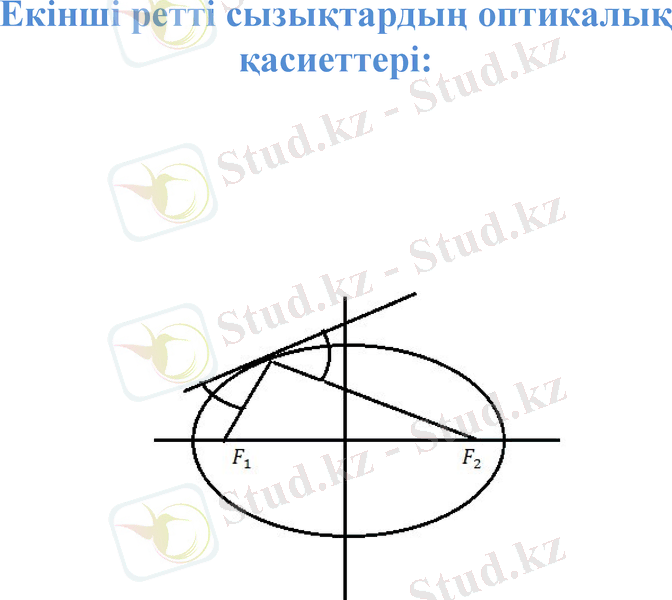
Екінші ретті сызықтардың оптикалық қасиеттері:

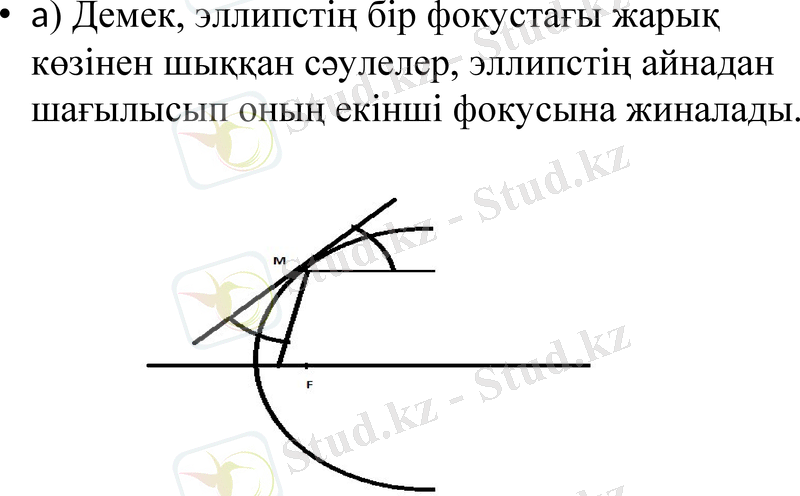
а) Демек, эллипстің бір фокустағы жарық көзінен шыққан сәулелер, эллипстің айнадан шағылысып оның екінші фокусына жиналады.

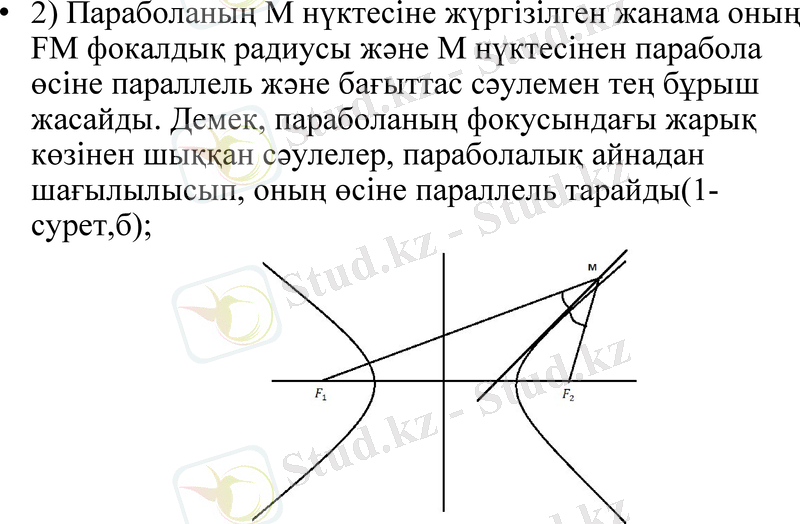
2) Параболаның М нүктесіне жүргізілген жанама оның FM фокалдық радиусы және М нүктесінен парабола өсіне параллель және бағыттас сәулемен тең бұрыш жасайды. Демек, параболаның фокусындағы жарық көзінен шыққан сәулелер, параболалық айнадан шағылылысып, оның өсіне параллель тарайды(1-сурет, б) ;

3) Гиперболаның М нүктесіне жүргізілген жанама оның фокустық радиустары және -мен тең бұрыш жасайды және бұрышқа іштей өтеді.

4) Демек, гиперболаның бір фокусындағы жарық көзінен шыққан сәулелер, гиперболаның айнадан шағылысып, оның екінші фокусынан шыққандай әсер қалдырады.

Мысал:

Қорытынды

Курстық жұмыстың тақырыбы «Екінші ретті сызықтар». Аналитикалық геометриядан екінші ретті сызықтар туралы мәлеметтер жинақталды. Екінші ретті сызықтардың оптикалық қасиеттері зерттелінді. Екінші ретті сызықтардың теңдеуі

Қисықты екі нүктеден қиып өтетін түзуді қиюшы түзу дейміз. Қиюшы түзу қозғалғанда оның екі нүктесі беттесіп жалпы бір нүктеге айналса, онда бұл түзу екінші ретті қисыққа жанама болады, ал жанама мен екінші ретті қисыққа ортақ нүктені жанасу нүктесі дейміз. Екінші ретті сызықтарға жүргізілген жанаманың теңдеуі қорытылды:

Екінші ретті теңдеулердің оптикалық қасиеттері қарастырылды. Тақырып бойынша төрт есеп шығарылды.

Ұқсас жұмыстар

Геодезиялық сызықтар

Туындылар

Синэкология– Бірлестіктер экологиясы

РЕНТГЕНДІК СПЕТРОСКОПИЯ

ТРАНСФОРМАТОР

ЭКОЛОГИЯ және ТҰРАҚТЫ ДАМУ. Экожүйедегі энергия

Диаграмманы құру алгоритмі

Функцияның дербес туындыларын табыңдар

Ақуыз және нуклеин қышқылдарының құрылысы және қызметі

Элементар функцияларды туындылау