Туынды ұғымы және экономикалық талдаудағы қолданылуы

Туындының экономикада қолдануы

Туынды ұғымы

ХVІІ ғасырда пайда болды

Белгіленулерін Лагранж енгізген

Туындыны дифференциалдау деп атаған Лейбниц болды

Өсімшені белгілеу үшін гректің

әріпін қолданған Эйлер болды

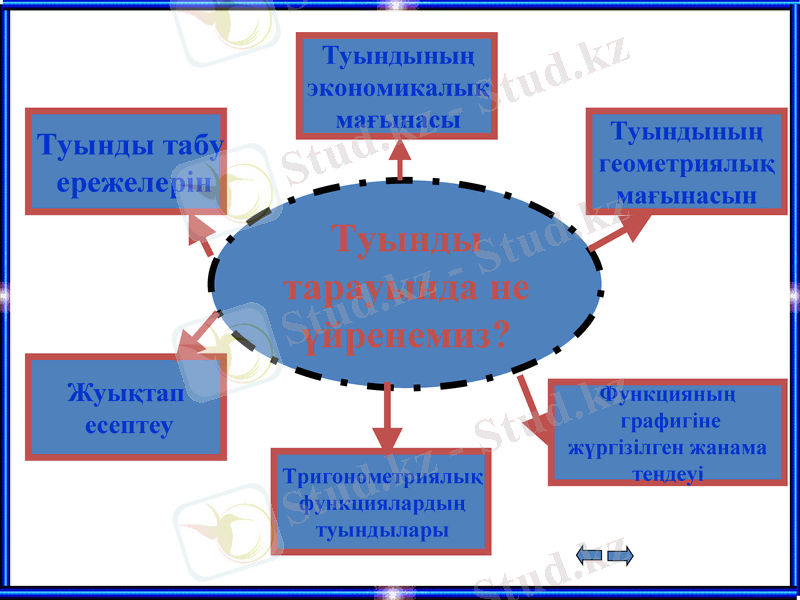
Туынды

тарауында не

үйренемиз?

Туындының

экономикалық

мағынасы

Туындының

геометриялық

мағынасын

Жуықтап

есептеу

Функцияның

графигіне

жүргізілген жанама

теңдеуі

Тригонометриялық

функциялардың

туындылары

Туынды табу

ережелерін

Туынды - дифференциалдық есептеулердің х аргументі өзгерген кездегі f(x) функциясының өзгеру жылдамдығымен сипатталатын негізгі түсінігі. Кез келген х үшін қатынасының шегі арқылы анықталатын функция -Туынды деп аталады және y΄, f΄(x), түрінде белгіленеді. Туындысы бар функция үзіліссіз. Берілген аралықтың барлық нүктелерінде Туындысы болмайтын үзіліссіз функциялар да болады. “ Туынды” терминін (1797) және оның белгіленулерін (1770, 1779) Ж. Лагранж, ал түрінде жазылуын Г. Лейбниц енгізген (1675) .

Туынды есептеу ережелері Ереже: Егер U және V функцияларының х нүктесінде туындылары бар болса, онда U+V функциясының х нүктесіндегі туындысы бар және ол (U+V) ' = U'+ V' былай анықталынады. Дәлелдеу үшін туынды анықтамасы мен туындыны табу алгоритімін қолданамыз. Екі функцияның қосындысы U(x) + V(x) =F(x) деп алып х-ке өсімшесін береміз, сонда ∆F(x) =F(x+∆x) -F(x) =U(x+∆x) - U(x) + V(x+∆x) -V(x) функция өсімшесін ∆х-ке бөлсек

Туындының функцияны зерттеуде қолданылуы

Туындының көмегімен функцияның кризистік нүктелерін, өсу, кему аралығы, функцияның максимум минимумдары анықталады

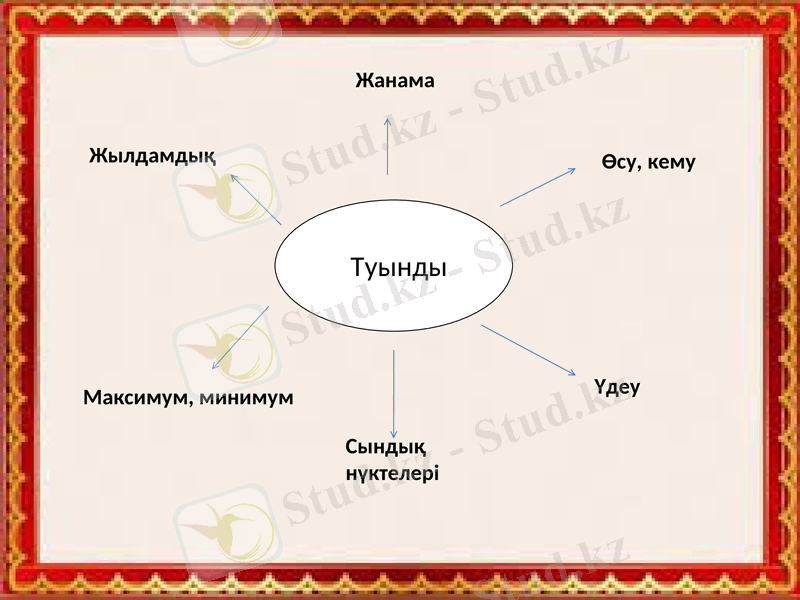
Туынды

Үдеу

Сындық нүктелері

Максимум, минимум

Өсу, кему

Жанама

Жылдамдық

Туындының экономикада қолданылуы

Туындының экономикада қолданылуының кейбір мысалдарын карастырамыз. Өндіру және тұтыну, сұраныс және ұсыныс теорияларының негізгі заңдары осы бөлімде келтірілген тұжырымдарға негізделеді.

Алдымен Ферма теоремасының экономикалық қолдануына тоқталайық.

Ферма теоремасы. Егер X аралығында дифференциалданатын у=ƒ(х) функциясы осы аралықтың ішінде жатқан бір х0 нүктесінде өзінің ең үлкен немесе ең кіші мәнін қабылдаса, онда оның туындысы х0 нүктесінде нөлге тең болады: ƒ''(хо) = 0.

Өндіру теориясының негізгі заңдарының бірі былай айтылады:

Өндірушіге тиімді тауар көлемі шектік шығын мен шектік табыстың теңдігімен анықталады.

Өнім көлемі х-ке тәуелді табыс функциясы - 0(х), пайда функциясы - С(х), ал шығын функциясы -S(х) болсын. Сонда С(х) = D(х) - S(х) . Әрине, пайда С(х) максималды мән алатын өнім көлемі х = х0 өндірістің тиімді деңгейі болады. Сондықтан Ферма теоремасы бойынша бұл нүктеде С'(х0) = 0, С'(х) =D(х) -S(х) болғандықтан D'(х0) =S'(х0) . Сонымен жоғарыда айтылған экономикалық зандылыққа келдік

Өңдіріс теориясының басқа бір маңызды ұғымы - орта шығындары ең аз (минимальді) болатын тиімді өндіріс деңгейі. Сәйкес экономикалық заң былай айтылады: орта және шектік шыгындардың теңдігімен ең тиімді өндіріс деңгейі анықталады.

Бұл шартта Ферма теоремасының салдары ретінде айтылады. Егер S(х) - х өнім көлеміне тәуелді шығын мөлшері болса, онда S(х) /х, яғни тауарды шығарудағы шығын көлемінің тауар санына қатынасы орта шығынды береді. Бұл шаманың минимумы оның күдікті нүктесінде болады. Сондықтан

(S(х) /х) '= S' (х) •х - S(х) /х2=0 → S' (х) •х - S(х) =0 →S' (х) = S(х) /х

яғни минимум (тиімді өндіріс деңгейі) орта жөне шектік шығында өзара тең болатын х - тің мөнінде қабылданады.

Функция графигінің дөңестік ұғымының да экономикалық мағынасы бар. Ең көп таралған экономикалық зандылықтарды бірі - кемімелі табыс заңы былай айтылады: Өндіріс өскен сайын әрбір жаңа ресурстан (еңбек ресурсын, технологиялық, ресурс алынған қосымша өнім бір уақыттан кейін кеми бастайды. Басқа сөзбен айтқанда, егер Δх -ресурс өсімшесі, ал Δу - шығатын өнім өсімшесі болса, онда Δу/Δх шамасы х өскен сайын кемиді.

Сонымен, кемімелі табыс заңы былай айтылады: Қолданылған ресурсқа тәуелді өнім көлемін беретін у = ƒ(х) функциясы графигінің дөңестігі жоғары бағытталған.

Экономикалық теорияның басқа бір іргелі ұғымы - ол пайдалылық функциясы U = U(х) . Мұнда х-тауар, ал U -пайдалылық. Бұл шама жеке тұтынушы үшін өте субъективті, ал жалпы қоғам үшін жеткілікті объективті болады. Кемімелі пайдалылық заңын былай айтады: Тауар көлемі өскен сайын бір уақытшан кейін әрбір жаңа тауардан алынатын қосымша пайдалылық кеми бастайды.

Кемімелі пайдалылық заңы сұраныс және ұсыныс теориясының математикалық зерттеулерінің негізі болады.

Туындының экономикалық мағынасы

Енді туындының экономикалық мағынасын көрсететін тағы бір ұғымды береміз.

Өндіріс шығындарын өндірілетін өнімнің мөлшері х-ке тәуелі функция ретінде карастырамыз. Өнімнің өсімі ∆х болса, оңі өндіріс шығынының өсімшесі ∆у, ал өнім бірлігіне жұмсалатын өндіріс шығынының орта өсімшесі ∆у /∆х болады. Сонда туынды у'= lim∆х →0∆у/∆х

өндірстің шекті шығынын береді және косымша өнімнің бірлігіне жұмсалатын қосымша шығынды жуықтап сипаттайды. Шекті шғындар өндіріс күші (шығарылатын өнім көлемі) х-ке тәуелді және тұрақты емес тек айнымалы өндіріс шығындарымен (шикізат, жанармай және т. б. ) анықталады. Осы сияқты шекті табыс, шекті өнім, шекті пайдалылық, шекті өнімділік және баска шекті шамаларды қарастыруға болады.

Туынды кайсыбір экономикалық объектінің басқа бір объектіге карағанда өзгеру жылдамдығын анықтайды

Туынды ұғымы функцияларды зерттеу кезінде, олардың графиктерін салуда қолданылады. Туындыны қолдана білу үшін біз дифференциалдық есептеудің бірнеше негізгі теоремаларымен танысуымыз керек.

f (x) > 0 және f < 0 болғанда функцияның қалай өзгеретінін қарастырамыз. Функцияның туындысы нолге тең немесе туындысы жоқ болатын анықталу облысының ішкі нүктелері сол функцияның кризистік нүктелері деп аталады. Функцияның графигін салғанда бүл нүктелер маңызды роль атқарады, өйткені тек сол нүктелер ғана функцияның экстремум нүктелері бола алады. Сәйкес пікірді тұжырымдаймыз - оны Ферма теоремасы деп аталады. Онымен кейін танысармыз.

Экстремум нүктелері деп максимум және минимум нүктелерін атаймыз.