Оқушыларды логикалық ойлауға математика

Физика-математика факультеті

Математика-5В010900

4 курс студенті

Әріп Мақпал Әбдіхалыққызы

ҚАЗАҚ МЕМЛЕКЕТТІК ҚЫЗДАР ПЕДАГОГИКАЛЫҚ УНИВЕРСИТЕТІ

Ғылыми жетекшісі: аға оқытушы Төлеуханова З. М.

Орта мектеп шеңберіндегі

математикалық логика

элеметтері

Кіріспе сөз.

Бүгінгі шәкірт ертеңгі азамат. Сол азамат бойында тапқырлықты, алғырлықты қалыптастыру мектеп қабырғасынан басталады.

Мақсаты:

Мектеп қабырғасында және де жоғары білім беру ордаларында оқытылатын математикалық логика элементтерінің кейбір тұстарын нақтылап, мысалдар келтіру арқылы айқындап көрсету.

Бұл дипломдық жұмыс кіріспеден, 3 тараудан, 14 бөлімшеден, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.

I тарау Орта мектеп шеңберіндегі математикалық логика элементтерін оқытудың маңызды тұстары

II тарау Математикалық логиканың элементтері

III тарау Предикаттар мен кванторлар

Диплом жұмысының құрылымы:

I тарау

Орта мектеп шеңберіндегі математикалық логика элементтерін оқытудың маңызды тұстары

1. Математика сабағында оқушылардың логикалық ойлау қабілеттерін дамыту.

2. Математикалық логикалық байланыстар.

3. Логикалық есептер және оларды есептеудің жолдары.

4. Жиындар теориясын логикалық есептер шығаруда қолдану

5. Комбинаторика элементтерін есептер шығаруда қолдану

Мектеп курсында логика жеке пән ретінде - өтілмейді, логикалық білім мен дағдыларды қалыптастыруға барлық сабақтардың үлесі бар, олардың ішінде математика сабағының ара салмағы үлкен.

Логика - бұл адам ойлауының түрлері мен заңдары туралы, оның ішінде дәлелдеуге болатын пікірлердің заңдылықтары туралы ғылым.

Оқушылардың логикалық ойлауын дамыту үшін

есепті, жаттығуларды талдай білу іскерліктерін қалыптастыру;

сызба графиктік модель бойынша есеп объектілерінің арасындағы байланыстарды түсіндіру;

Есептегі нақты заттарды оның моделімен ауыстыру;

Пәнге деген қызығушылығын, сүйіспеншілігін арттыру;

Сыныпқа дұрыс психологиялық жағдай орнатуға мүмкіндік туғызу.

Оқушылардың оқудағы танымдық ізденімпаздығы мен белсенділігін қалыптастыру проблемаларын іс жүзінде шешудің әр түрлі жолдары бар:

оқып үйренуге және оқып игеруге деген оқушы қызығушылығын тудыру;

білімді дайын күйінде бермей, оқушының өзі білімді қарқынды ой еңбегін қажет ететін тапсырмаларды орындау арқылы жетуін ұйымдастыру;

жаңа білімнің мазмұнын жоспарлағанда оқушыға берілетін тапсырма оқушы қабілетін ұштайтындай, ойын, қиялын дамытатындай етіп әзірлеу;

оқушылардың білім алу нәтижелерін жүйелі талдап, бағалап отыру;

Математикалық ойлау ерекшеліктерін келесідей белгілер арқылы айқындауға болады .

1) логикалық тұжырымдар жүйесінің басымдылығы;

2) мақсатқа жетуде ең ықшамды жолды таңдай алу мүмкіндігінің жоғарылығы (ой ықшамдылығы) ;

3) ой жүгіртудің бөліктік айқындылығы;

4) символды дәлдікпен қолдану.

5) ой тұжырымдардың, пікірлердің нақты еместігін, дәлелдемелердегі қажетті буындардың толық еместігін байқау.

Практикалық іс-әрекет

Көрнекілік-бейнелік

Сөздік-логикалық

Ойлаудың түрлері мен формаларын дамыту

Оқушыларды логикалық ойлауға қалай үйретуге болады?

Оқушыларды логикалық ойлауға үйретуге бола ма?

Пәнаралық

байланыс

Қазақ тілі

математика

геометрия

психология

Химия

Физика

Салт - дәстүрлер

педагогика

Формальды

логика

Ықтималдықты

логика

Диалектикалық

логика

Математикалық

логика

Ғылыми пән ретінде логиканың бірнеше

нұсқалары дараланады:

Есептердің шешу барысында математикалық логиканың элементтерін пайдалану

Қатынастары бар есептердің шешу, яғни транзитивті болатын «кіші», «үлкен» және «тең», транзитивті емес, бірнеше қатынасы бар есептер.

Жарыстарға және спорт түріне байланысты есептер.

Өткелге байланысты, жүзетін құралдардың жүк көтерімділік және жолаушылардың санымен шектелетін есептер.

«Граф» тәсілімен шешілетін есептер.

Арифметикалық ребустер құрастыру мен оларды шешу.

Логикалық ойын есептері.

Бөшкедегі су.

Жұмыскерді жұмысқа алу үшін бай оған бір сыннан өтуді ұсынды:

- Берілген бөшкені су құйып, орталау керек. Бірақ ішіндегі суды өлшеуге не таяқ, не жіп, не басқа да нәрселерді қолдануға болмайды-депті.

Жұмыскер бұл тапсырманы орындап, жұмысқа алынған. Ол оны қалай орындады?

Бөшкеге су тура ортасына дейін құйылғанын оны еңкейту арқылы байқауға болады. а) суретте бөшкені еңкейткенде су беті бөшке бетінің шеті мен түбінің жоғарғы нүктесінің бір деңгейде жатқанын көреміз, бұл бір біріне диаметральді қарама-қарсы жатқан нүктелер арқылы өткен су бетінің жазықтығы бөшкені тура екі бөлікке бөлінгенін көрсетеді.

Ал қалған б) және в) жағдайларында түбі не ашық, не судың астында болатыны байқалады.

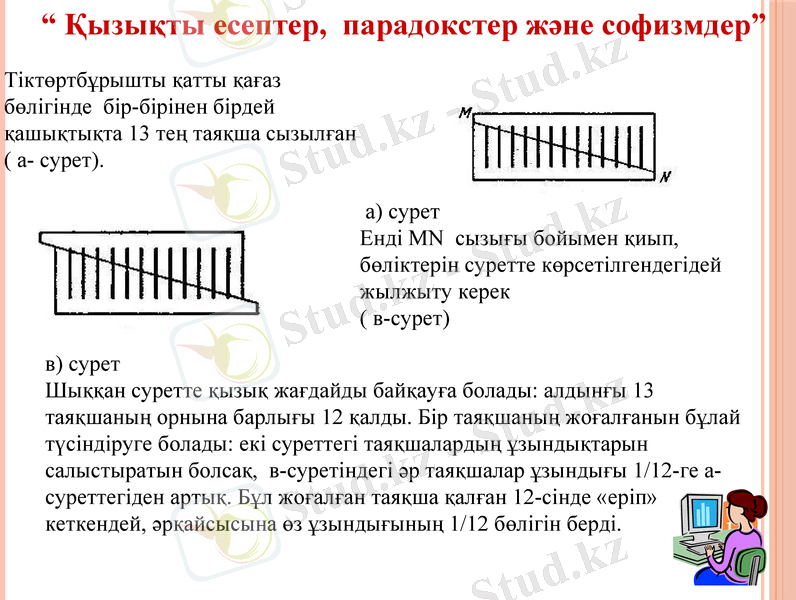
Тіктөртбұрышты қатты қағаз бөлігінде бір-бірінен бірдей қашықтықта 13 тең таяқша сызылған ( а- сурет) .

а) сурет

Енді МN сызығы бойымен қиып, бөліктерін суретте көрсетілгендегідей жылжыту керек

( в-сурет)

в) сурет

Шыққан суретте қызық жағдайды байқауға болады: алдынғы 13 таяқшаның орнына барлығы 12 қалды. Бір таяқшаның жоғалғанын бұлай түсіндіруге болады: екі суреттегі таяқшалардың ұзындықтарын салыстыратын болсақ, в-суретіндегі әр таяқшалар ұзындығы 1/12-ге а-суреттегіден артық. Бұл жоғалған таяқша қалған 12-сінде «еріп» кеткендей, әрқайсысына өз ұзындығының 1/12 бөлігін берді.

“ Қызықты есептер, парадокстер және софизмдер”

Графтар тәсілі

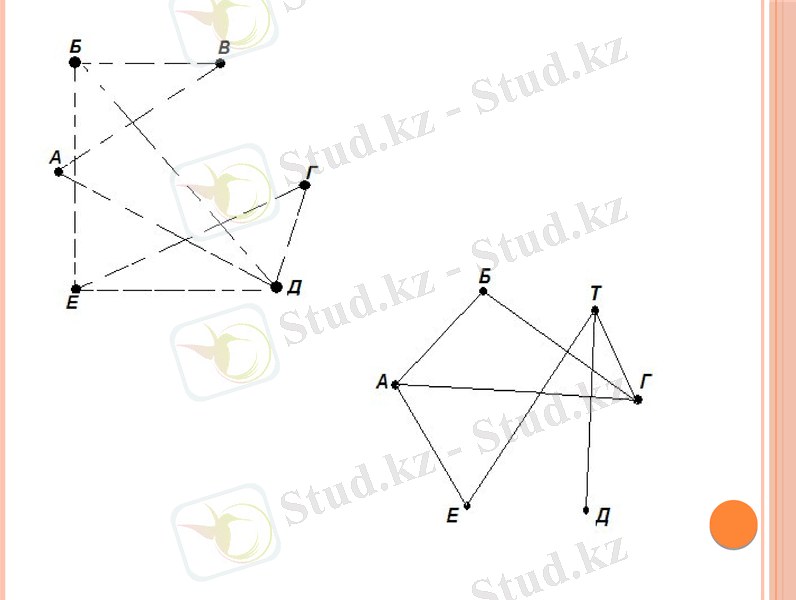
Сынып біріншілігі. Үстел тенисі бойынша сынып біріншілігіне 6 бала қатысты: Айгүл, Бекжан, Тимур, Гүлім, Дамир, Еркін. Біріншілік айналу жүйесі бойынша өткізіледі - жарысқа қатысушы әрбір адам қалғандарымен бір-бір рет ойнап шығады. Бұған дейін бірнеше ойын өткізілген болатын: Айгүл Бекжанмен, Гүліммен Еркінмен; Тимур, бұрын айтылғандай, Айгүлмен және Гүліммен; Тимур- Гүліммен, Дамир - Тимурмен және Еркін - Айгүлмен және Тимурмен ойнаған. Бұған дейін неше ойын ойналған және тағы неше ойын қалды? Талқылау. Берілген есепті схема түрінде кескіндейік. Қатысушыларды нүктемен кескіндейміз: Айгүлді - А нүктесімен, Бекжанды - Б нуктесімен т. с. с. Егер қатысушылардың екеуі ойнап кеткен болса онда оларды кескіндейтін нүктені кесінділермен қосамыз. Сонда 1-суретте көрсетілгендей схема шығады. Бұған дейін өткізілген ойындар саны қабырғалар санына тең, яғни 7. Өткізілуге тиісті ойындардың санын табу үшін, тағы бір граф сызайық, оның төбелері бұрынғыдай, бірақ қабырғалары бір-бірімен әлі ойнамаған балаларды қосатын кесінділер болады, 2-сурет. Бұл графтың қабырғасы 8 болып шықты, демек, әлі 8 ойын өткізу керек: Айгүл - Тимурмен және Дамирмен, Бекжан - Тимурмен, Дамирмен және Тимурмен т. с. с. теннис ойнауы керек. Графтарды біз өте жиі пайдаланамыз.

1. Жұлдызшаның орына сан қойып, көбейтуді орында:

* 2 *

2 7

3 6 * 8

* * * *

* * * * *

2. 0, 1, 2, 3 цифрларынан бірдей цифр қайталанбайтын барлық мүмкін төрт таңбалы сандарды жазыңдар. Мысалы 3 201 санын және т. б. құрастыруға болады. Алынған ең үлкен және ең кіші сандардың айырмасын неге тең? 3 210 - 1 023= 2 187

524 · 27 = 14 148

Әрбір сақинадағы сандардың қосындысы 55-ке тең болса, А қаншаға тең? 10

Арифметикалық ребустер құрастыру мен оларды шешу.

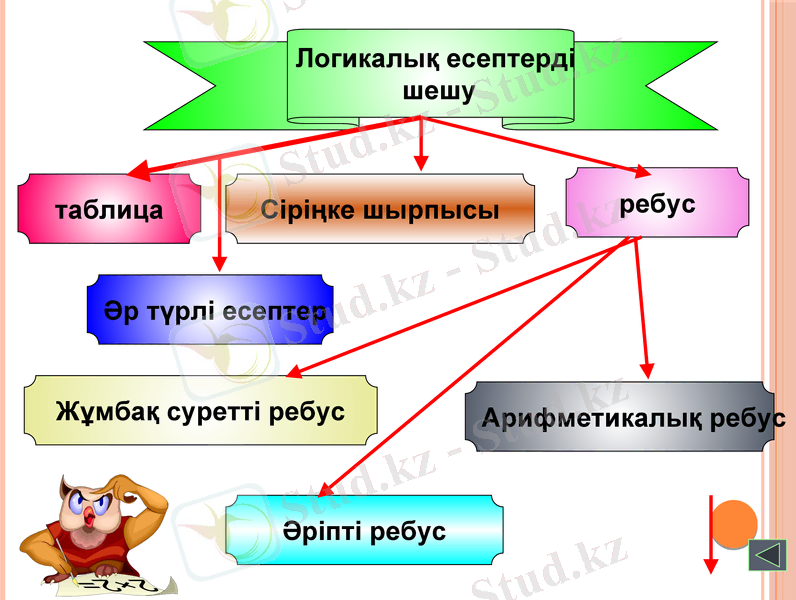
Логикалық есептерді

шешу

таблица

Сіріңке шырпысы

Әр түрлі есептер

Әріпті ребус

Арифметикалық ребус

ребус

Жұмбақ суретті ребус

Жиындар теориясын логикалық есептер шығаруда қолдану.

Есеп. Ойын-сауыққа барлығы 38 жас жігіттер мен қыздар жиналған. Олардың 16-сы ән салады. Ал 17-сі би билейді, 18-і домбырада ойнайды. Ал олардың төртеуі ән де салады, би де билейді, үшеуі ән де салады, домбыра да тартады, бесеуі би де билейді, домбыра да тартады. Ал үшеуі ғана ән де салмайды, би де билемейді, домбыра да тартпайды. Сонда неше жастың бойында үш өнер де бар, неше жастың бойында тек бір ғана өнер бар?

Шешуі: Бойында үш өнер де бар жастарды x деп белгілейміз. Сонда тек әнмен шұғылданатын жастар: 16 - /4+x+3/ - 9 - x, тек бимен шұғылданатын жастар:

17 - /4+x+5/ = 8 - x.

Тек домбырамен шұғылданатын жастар: 18 - /3+x+5/ = 10 - x.

Егер есептің шарты бойынша салынған суретті пайдаланып, теңдеу құрсақ:

3 + /9-x/ + /8-x/ +/10-x/ + 4 +3 + 5 +x = 38.

Теңдеуді шешіп, x = 2 аламыз.

Сонда

9 - 2 = 7;

8 - 2 = 6;

10 - 2 = 8;

7 + 6 + 8 = 21.

Жауабы: Екі жастың бойында үш өнер де бар, ал жиырма бір жастың бойында тек бір ғана өнер бар.

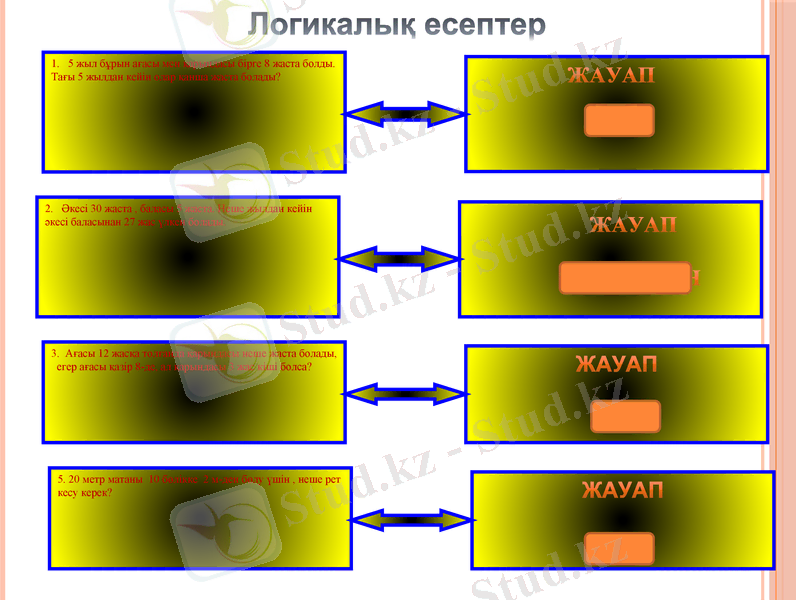
Логикалық есептер

жауап

ешқашан

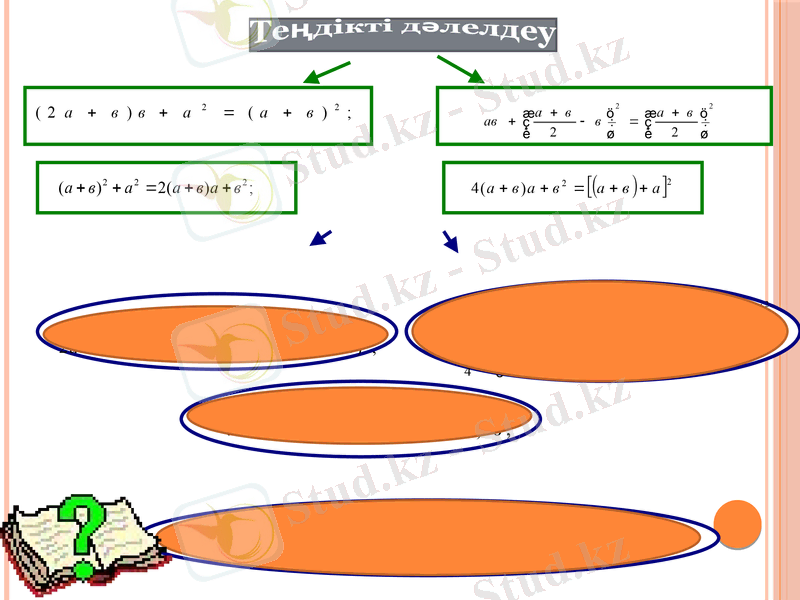
Теңдікті дәлелдеу

Үш адам 24000 ливрға үй сатып алғысы

келді. Олар былай келісті: біріншісі

жарты ақшасын береді; екіншісі үштен

бірін береді, ал үшіншісі қалған бөлігін

береді. Әрқайсысы қанша бермек?

Бір адам бір ұстазға келіп, неше

шәкірттің бар, ұлымды саған оқытуға

бергім келіп еді депті. Сонда ұстаз т

ұрып: егер маған өзімде қанша шәкірт

бар болса, соншасы және оның

жартысы, сондай- ақ ширегі, оның

үстіне сенің ұлың келсе, менде шәкірт

саны 100 болар еді деп жауап беріпті.

Ұстаздың неше шәкірті болған?

«Егер бір санды 20-ға қоссақ және

сол санды 100-ден алсақ, сонда

шыққан қосынды сонда шыққан а

йырмадан 4 есе артық болады.

Белгісізді табу керек. »

Құпия хат

жауаптары

22x=792

х=36

I-ші:

II-ші:

III-ші:

Жауабы:

20+x=(100+x) 4

20+x=400-4x

5x=380

x= 76

Математикалық логиканың (басқаша логика алгебрасы) деп аталады. Ол алғаш рет Джордж Бульдің еңбектерінде пайда болды. Логика дұрыс ойлаудың заңдары мен жүйелі де дәлелді түрде пайымдауға қойылатын талаптар туралы ғылым. Анықтама, дәлелдеме, пайымдау, жіктеп саралау тағы басқа логикалық амалдарды әрбір оқушы өзінің ойлау қызметінде қолданып отырады. Оқушы анықтамаларды жаттап, теоремаларды дәлелдей отырып дәлелдеу мен бекерлеудің мәні, түрлері және оларды қалай дұрыс қолдану туралы әдетте біле бермейді. Негізгі логикалық терминдер болып табылатын «және», «немесе», «егер, болса, онда . . . », «емес», «сонда» және «тек сонда ғана» тағы басқа арқылы құрастырылған.

Мынадай мысалдарды қарастырайық:

“102 саны жұп немесе 3 - ке бөлінеді”;

“Мен театрға немесе қонаққа барамын”;

“Ол жұмысқа автобуспен немесе трамваймен келеді”.

Бұл келтірілген пікірлер күрделі, олардың бәрінің формасы “А немесе В” түріндегі болады. “А немесе В” формасындағы пікірді А мен В пікірлерінің дизъюнкциясы деп атайды.

Ұқсас жұмыстар

Математика сабағында бастауыш сынып оқушыларының логикалық ойлау және есептеу дағдыларын дамыту

Оқушылардың логикалық ойлау қабілетін дамыту және пәнге деген қызығушылығын арттыру

Сандар әлеміне саяхат

Орта мектепте геометрияны оқытудың жалпы әдістемелік мәселелері

Конкурстық есептер

Пифагор теоремасы туралы

Математикадан сыныптан тыс жұмыстарды ұйымдастыру технологиясы

Есептеп дұрыстығын тексер

БИОЛОГИЯ ПӘНІ БОЙЫНША ОЛИМПИАДАЛЫҚ ТАПСЫРМАЛАРДЫ ДАЙЫНДАУДЫҢ ЕРЕКШЕЛІКТЕРІ МЕН МӘНІ

ОЙЛАУ ТУРАЛЫ ЖАЛПЫ ТҮСІНІК ТУРАЛЫ

Пәндер