Анықталмаған интеграл

Презентация қосу

Қазақстан Республикасы Білім және ғылым
министрлігі
Павлодар мемлекеттік педагогикалық университеті

КУРСТЫҚ ЖҰМЫС

Орындаған: Тусупова К.Е
Тексерген: профессор Найманов Б.А
Жұмыстың тақырыбы:
«Анықталмаған интеграл және
оны табудың әртүрлі тәсілдері»
Жұмыстың
Жұмыстың
мақсаты:
мақсаты:

Интеграл ұғымына жалпы сипаттама бере отырып, оның
түрлеріне және оның ішінде анықталмаған интегралға
тоқталу. Оны табудың тәсілдері мен әдістерін
қарастырып, мысалдар келтіру.
Курстық жұмыстың міндеті:
- Анықталмаған интеграл және оның
қасиеттерін ашып көрсету;
- Анықталмаған интегралдарды
есептеу әдістерін көрсету;
- Тәжірибелік-эксперименттік жұмыс
Курстық жұмыстың зерттеу обьектісі:
Математикалық анализ.
Интеграл туралы жалпы
ұғым
Интеграл (лат. Іnteger – бүтін) – математиканың маңызды
ұғымдарының бірі. Интеграл ұғымы бір жағынан –
туындысы бойынша функцияны іздеу (мысалы, қозғалған
нүктенің жүріп өткен жолын өрнектейтін функцияны сол
нүктенің жылдамдығы бойынша табу), екінші жағынан –
аудан, көлем және доға ұзындығын өлшеу, күштің белгілі
бір уақыт ішінде атқарған жұмысын табу, т.б.
қажеттіліктерден пайда болды. Осыған қатысты интеграл
анықталмаған интеграл және анықталған интеграл болып
ажыратылады. Міне, осыларды есептеу интегралдық
есептеудің міндеті болып саналады.
F’(x)=f(x) және ʃ f(x)dx = F(x) + C екенін ескере отырып анықталмаған
интегралдың қасиеттерін қарастырамыз
Анықталмаған интеграл, оның
қасиеттері
F(x) функциясы дифференциалдау деп берілген алғашқы F(x)
функциясының F’(x)= f(x) туындысын немесе df(x)=f(x)dx.
Дифференциалын табу амалын айтамыз.
Сол амалға кері амал, яғни F’(x) болып табылатын берілген f(x)
үшін алғашқы F(x) функциясын табу амалы f(x)-ті интегралдау
деп аталады.
F (x)-ті интегралдау амалын көрсету үшін ʃ символы
қолданылады да, былай жазылады: ʃ f(x)dx.
Осы ʃ f(x)dx берілген f(x) функциясының барлық алғашқы
функцияларының жиынын бейнелейді және f(x)-тен
анықталмаған интеграл деп аталады.
Демек, анықтамаға сәйкес ʃ f(x)dx = F(x) + C болады. Бұл
формуладағы F(x) функциясы f(x)-тың белгілі бір алғашқы
функциясы, С-кез келген тұрақты.
Сонымен бірге f(x) – интеграл астындағы функция, ал f(x)dx –
интеграл астындағы өрнек деп аталады.
ʃ - символы ұзартылып алынған латын алфавитіндегі S әріпі, ол
символды интегралдың белгісі деп атайды.
Функцияны интегралдау және олардың алғашқы
функцияларының қаиеттері жайындағы ілім интегралдық есептеу
деп аталады.
Анықталмаған
интегралды іздеу амалы
немесе дифференциалдық
теңдеулерді шешу.
Осыған сай
дифференциалдау
формулалары мен
ережелеріне сүйене
отырып, интегралдаудың
формулалары мен
ережелерін алуға болады.
Анықталмаған интеграл
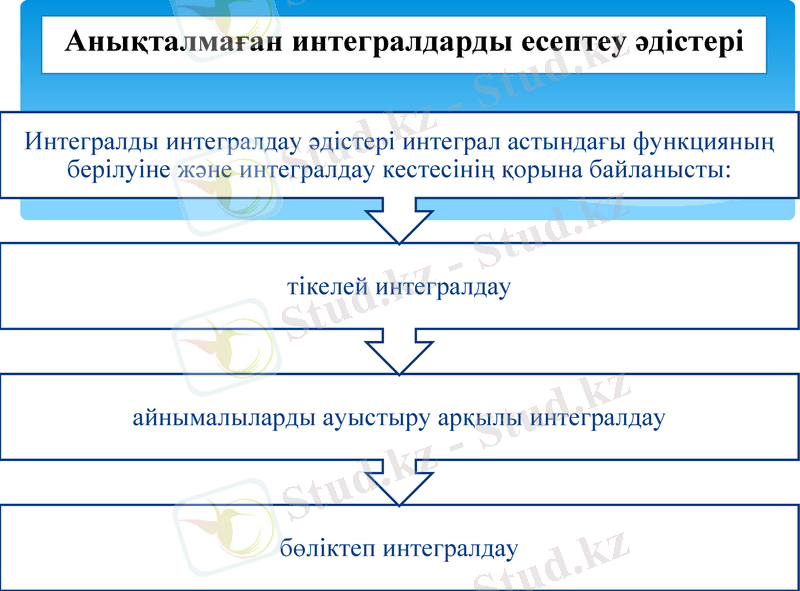
Анықталмаған интегралдарды есептеу әдістері
1.Тікелей интегралдау.Көптеген функцияларды
анықталмаған интегралдың қасиеттері мен интегралдау
кестесіне сүйеніп тікелей интегралдауға болады. Тікелей
интегралдау тәсіліне бірнеше мысалдар келтірейік.

Мысалы -1. интегралын есептеу керек.

Шешуі. болған жағдайда III формуланы
қолданамыз:
2. Айнымалыны
ауыстыру әдісі

∫ х√х-3dx Квадрат түбірден
құтылу үшін √х-3=t деп жаңа t
айнымалысын енгіземіз. Сонда
x=t²+3 және dx=2t dt.
Ауыстыруды енгізген соң,
аламыз:
∫ x√x-3xdx= ∫ (t²+3) t2tdt= ∫
(2t⁴+6t²)dt= 5/2+2 (x-3)3/2+C
3. Бөліктеп интегралдау
Қорытын
ды
Интеграл (лат. Іnteger – бүтін) – математиканың
маңызды ұғымдарының бірі. Интеграл ұғымы бір
жағынан – туындысы бойынша функцияны іздеу
(мысалы, қозғалған нүктенің жүріп өткен жолын
өрнектейтін функцияны сол нүктенің жылдамдығы
бойынша табу), екінші жағынан – аудан, көлем
және доға ұзындығын өлшеу, күштің белгілі бір
уақыт ішінде атқарған жұмысын табу, т.б.
қажеттіліктерден пайда болды. Осыған қатысты
интеграл анықталмаған интеграл және
анықталған интеграл болып ажыратылады. Міне,
Назарларыңызға рахме

Ұқсас жұмыстар

Анықталған интеграл және оның қолданылулары

Меншіксіз интегралдар

Алғашқы функция және интеграл

Қос интеграл

Интегралдық есептеу термині мен интеграл таңбасы Лейбництен бастап қолданылып

Анықталмаған интеграл қасиеттері

Анықталған интегралдың қолданылуы

Алғашқы функция және интеграл тарауын қайталап, бекіту

Тікелей интегралдау деп кестеде келтірілген анықталмаған интегралдар мен анықталмаған интегралдардың негізгі қасиеттерін қолданып алғашқы функцияларды табу

Геометриялық және физикалық есептерде интегралды қолдану. 11 сынып

Пәндер