Биномдық үлестірім

Скачать

Биномдық үлестірім

Оқу мақсаттары:

Сынақтар жүргізудің Бернулли схемасының шарттарын біледі;

Бернулли формуласын біледі;

Биномдық үлестірімнің мәнін түсінеді.

Мысал:

1 ғана жауабы дұрыс болатындай 5 жауабы бар 6 сұрақтан тұратын тест берілген.

Сұрақ 1. Жауап:

Сұрақ 2. Жауап:

Сұрақ 3. Жауап:

Сұрақ 4. Жауап:

Сұрақ 5. Жауап:

Сұрақ 6. Жауап:

Оқушы сұрақтардың жауабын кездейсоқ таңдайды. Дұрыс жауапты таңдаудың үлестірім заңдылығын анықтау қажет.

Дұрыс жауаптар саны

Ықтималдылығы

Кездейсоқ шама Х={дұрыс жауаптар саны}

Қандай да бір ықтималдықпен жеті мән қабылдайды:

Үлестірім заңдылығы

2 дұрыс жауап болуының ықтималдығы қандай?

Ықтималдығын есептейік

Әрбір сұрақтағы жауаптың дұрыс болуының

ықтималдығы 0, 2-тең

Барлық дұрыс жауаптар саны - 2.

Ал қате жауаптар саны - 4.

6 жауаптың ішінен 2 дұрыс жауапты таңдау

тәсілінің санын ескереміз.

3 дұрыс жауап болуының ықтималдығын

есептейік:

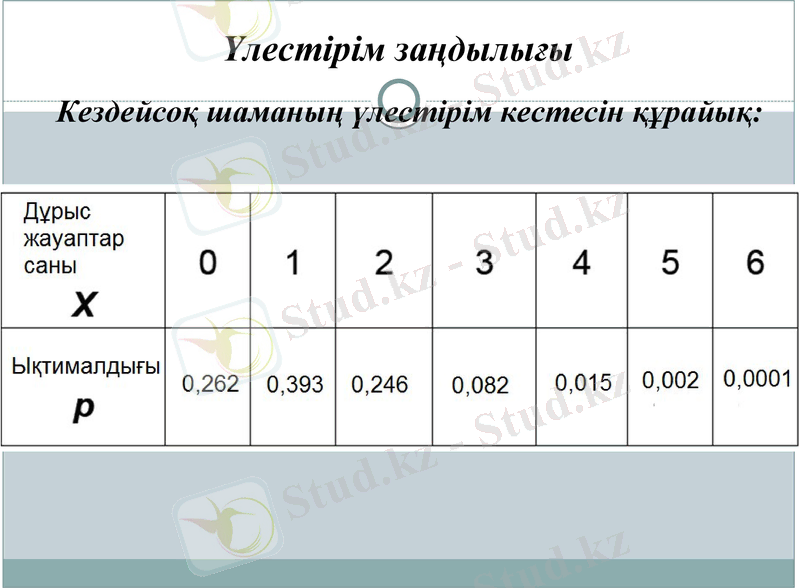
Үлестірім заңдылығы

Кездейсоқ шаманың үлестірім кестесін құрайық:

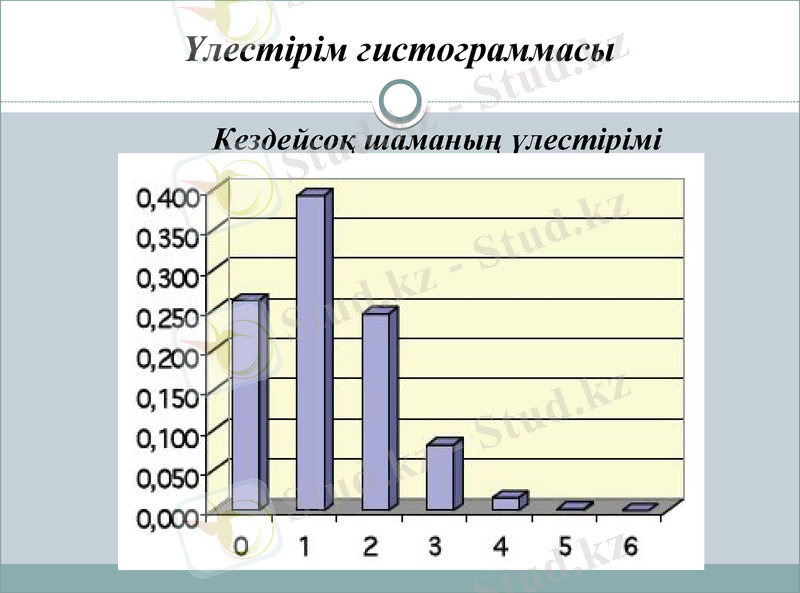
Үлестірім гистограммасы

Кездейсоқ шаманың үлестірімі

Сынақтар жүргізудің Бернулли

схемасының шарттары

Бернулли схемасы - төмендегі шарттардың

орындалуын қажет ететін сынақтар жүргізудің

схемасы:

Қажетті саны бойынша сынақтар жүргізіледі;

Жүргізілген сынақтардың өзара тәуелсіз болуы;

Әрбір сынақ нәтижесі сәтті не сәтсіз болуы;

Әрбір сынақ нәтижесінің ықтималдығы тұрақты

болуы.

Қажетті алты сынақ жүргізіледі;

Жүргізілген сынақтардың өзара тәуелсіз;

Әрбір сынақ нәтижесі сәтті не сәтсіз болады;

Әрбір сынақтың бес нәтижесі бар, олардың біреуі ғана дұрыс жауап. Әрбір сынақта дұрыс жауаптың шығу ықтималдығы 0. 2,

яғни тұрақты болады.

Біз қарастырған мысал үшін барлық шарттар сақталған, яғни:

Бір сынақтың «сәтті» болуының ықтималдығы

Бір сынақтың «сәтсіз» болуының ықтималдығы

Барлық сынақтар саны

п сынақтағы «сәтті» саны

п сынақтағы k сәтті болу ықтималдығы

Ықтималдықты есептеу

Әдіс 1. Формуланы қолдану

Биномдық үлестірімде ықтималдылық келесі формула бойынша есептелінеді:

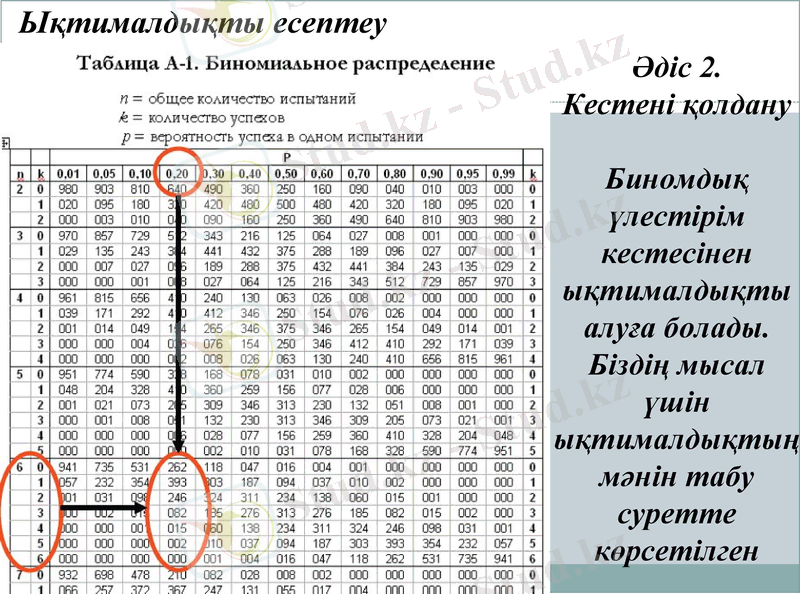
Ықтималдықты есептеу

Әдіс 2.

Кестені қолдану

Биномдық үлестірім кестесінен ықтималдықты алуға болады.

Біздің мысал үшін ықтималдықтың мәнін табу суретте көрсетілген

Ықтималдықты есептеу

Әдіс 3. Компьютерді қолдану

EXCEL-де ықтималдықтың мәнін табу жолы көрсетілген:

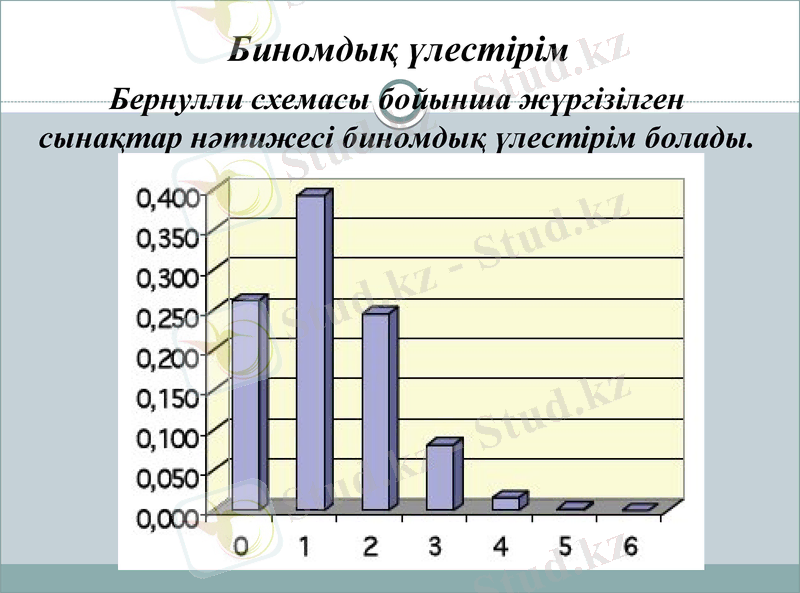
Биномдық үлестірім

Бернулли схемасы бойынша жүргізілген

сынақтар нәтижесі биномдық үлестірім болады.

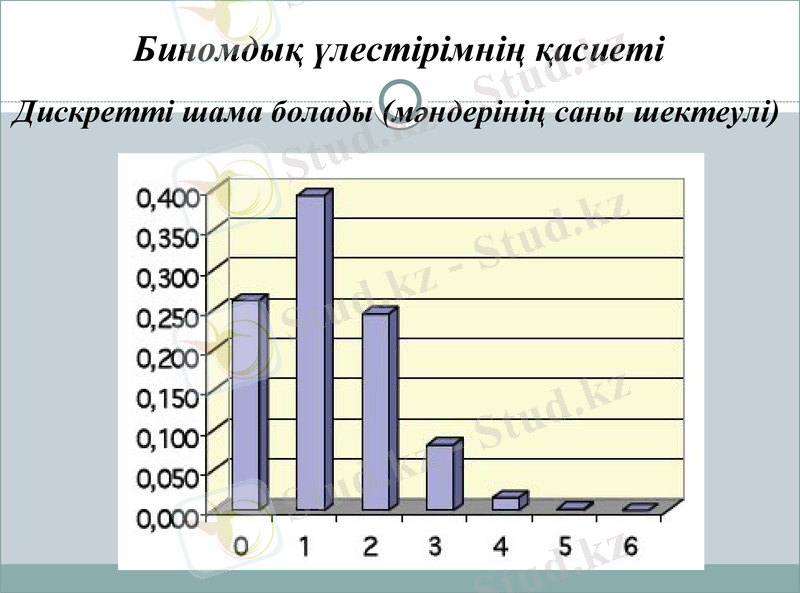
Биномдық үлестірімнің қасиеті

Дискретті шама болады (мәндерінің саны шектеулі)

Сандық сипаттамалар

Математикалық күтім

Дисперсия

Стандартты ауытқу

Мысал бойынша:

Математикалық күтім

Дисперсия

Стандартты ауытқу

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс