Геодезиялық сызықтар

Қазақстан Республикасы Білім және Ғылым Министрлігі Семей қаласының Шәкәрім атындағы мемлекеттік университеті

«Геодезия және құрылыс кафедрасы»

СӨЖ

Тақырыбы: Геодезиялық сызықтар. Клеро теңдеуі.

Орындаған: Серікқанов Ә. М.

Тобы: ГК-711

Тексерген: Шакерова Қ. Б.

Семей 2019

Жоспары:

І Кіріспе

ІІ Негізгі бөлім

Геодезиялық сызықтар

Геодезиялық сызықтарға тән қасиет

Клеро теңдеуі

Клеро теоремасы

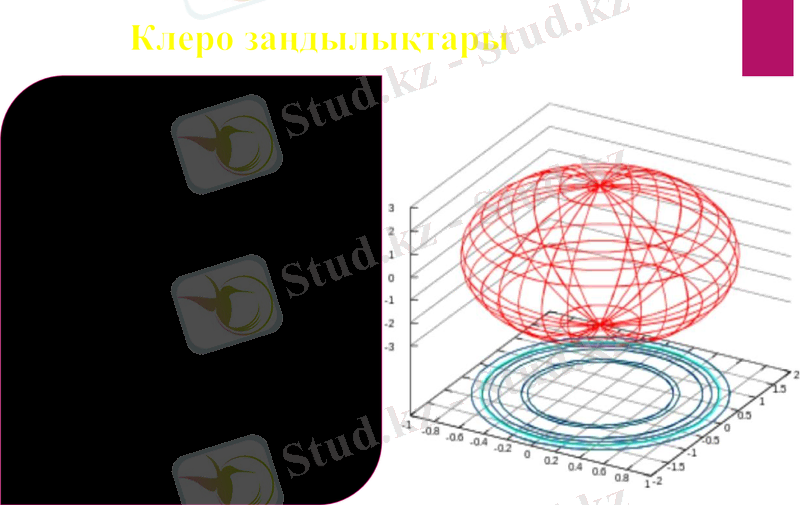
Клеро заңдалықтары

ІІІ Қорытынды

IV Пайдаланылған әдебиеттер тізімі

Кіріспе:

Геометрияда геодезиялық қисық-бұл беттің екі нүктесінің арасындағы қысқа жолды немесе жалпы мағынада римандық алуан түрлілікті көрсететін қисық. Бұл "түзу сызық" ұғымын жалпы қондырғыға жинақтау. "Геодезиялық" термині геодезия, жердің өлшемдері мен нысанын Өлшеу туралы ғылымнан шыққан. Бастапқы мағынада геодезиялық жер бетіндегі екі нүкте арасында қысқа жол болды. Сфералық жер үшін бұл үлкен шеңбердің сегменті.

Бетте жатқан сызықтың әрбір нүктесіндегі геодезиялық қисықтығы 0-ге тең болмса онда ол сызықты геодезиялық сызық дейді.

Жатық бет r=r (u, v) теңдеумен онда жатқан сызық u=u(s), v=v(s) теңдеуімен беріледі. Геодезиялық сызықтың әрбір нүктесіндегі қисықтың векторы мен бет нормалы кллинар болады. . Геодезиялық сызықтардың кез келген доғасы қарастырылатын беттегі ең қысқа аралық бола алмайды.

Клеро теоремасы-сфероид параметрлері, оның бетіндегі ауырлық күші мен гравитациялық әлеуеттің ыдырау коэффициенттері арасындағы тәуелділікті сипаттайтын заң. Математиканың алынған теңдеуі айналу беттеріндегі геодезиялық сызықтары Клеро теңдеуі деп аталады.

Геодезиялық сызықтар

жазықтықта - ТҮЗУЛЕР

ал сферада - ҮЛКЕН ДӨҢГЕЛЕКТЕР түрінде болады.

дөңгелек цилиндрде - ВИНТТІК СЫЗЫҚТАР

Геодезиялық сызықтар

Геодезиялық сызықтар - берілген беттегі мейлінше кіші доға ұштарының ең қысқа аралықтарын қосатын сызықтар. Геодезиялық сызықтар жазықтықта - түзулер, дөңгелек цилиндрде - винттік сызықтар, ал сферада - үлкен дөңгелектер түрінде болады. Геодезиялық сызықтардың кез келген доғасы қарастырылатын беттегі ең қысқа аралық бола алмайды.

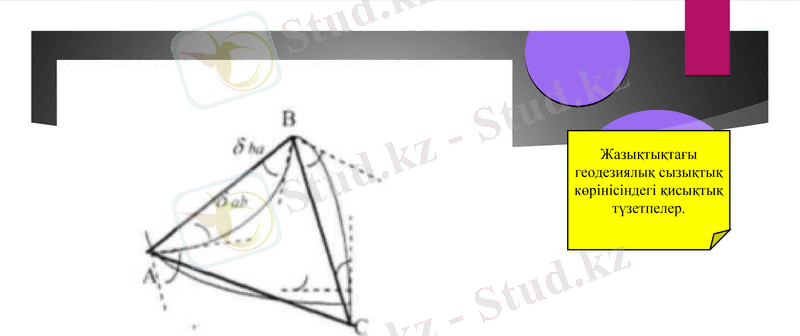
Жазықтықтағы геодезиялық сызықтық көрінісіндегі қисықтық түзетпелер.

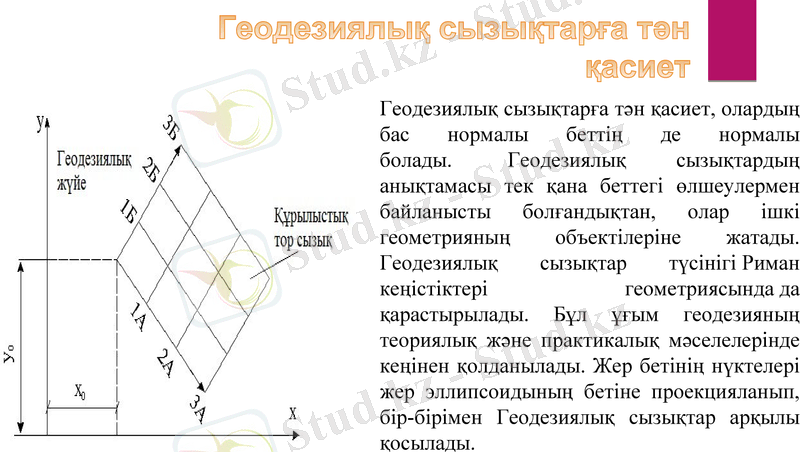
Геодезиялық сызықтарға тән қасиет, олардың бас нормалы беттің де нормалы болады. Геодезиялық сызықтардың анықтамасы тек қана беттегі өлшеулермен байланысты болғандықтан, олар ішкі геометрияның объектілеріне жатады. Геодезиялық сызықтар түсінігі Риман кеңістіктері геометриясында да қарастырылады. Бұл ұғым геодезияның теориялық және практикалық мәселелерінде кеңінен қолданылады. Жер бетінің нүктелері жер эллипсоидының бетіне проекцияланып, бір-бірімен Геодезиялық сызықтар арқылы қосылады.

Геодезиялық сызықтарға тән

қасиет

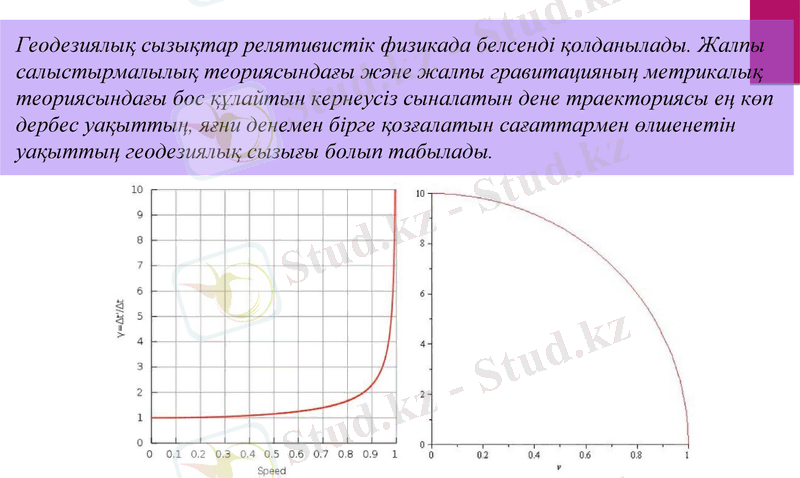
Геодезиялық сызықтар релятивистік физикада белсенді қолданылады. Жалпы салыстырмалылық теориясындағы және жалпы гравитацияның метрикалық теориясындағы бос құлайтын кернеусіз сыналатын дене траекториясы ең көп дербес уақыттың, яғни денемен бірге қозғалатын сағаттармен өлшенетін уақыттың геодезиялық сызығы болып табылады.

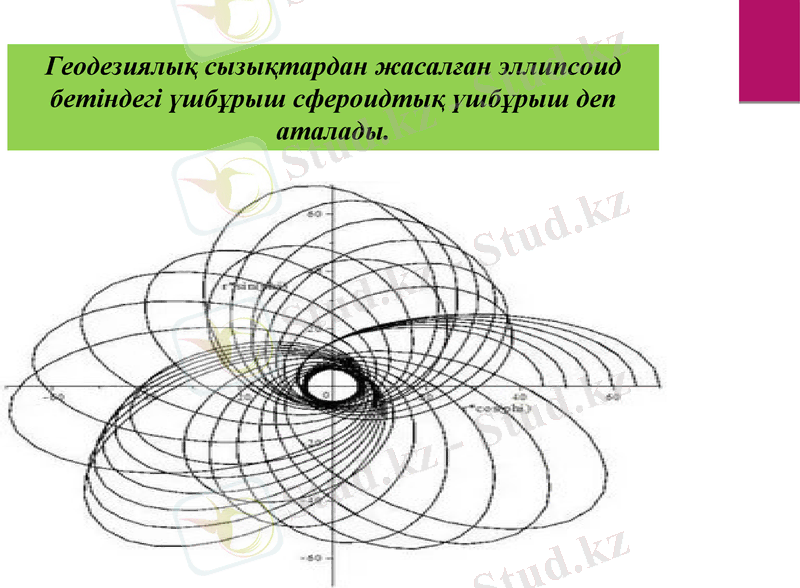
Геодезиялық сызықтардан жасалған эллипсоид бетіндегі үшбұрыш сфероидтық үшбұрыш деп аталады.

1773 жылы француз математигі және геодезист Клеро түр жүйесінің бірінші интегралын алды. Айналу беттеріндегі геодезиялық желілерді сипаттайды. Математиканың алынған теңдеуі айналу беттеріндегі геодезиялық сызықтары Клеро теңдеуі деп аталады.

Клеро теңдеуі

Клеро теңдеуі - y=xy'+f(y') түріндегі 1-ретті жай дифференциалдық теңдеу (мұндағы f - берілген дифференциалданатын функция) . Бұл теңдеуді тұңғыш рет француз математигі әрі астрономы А. Клеро (1713 - 1765) қарастырған (1734) . Клеро теңдеуі шекті түрде интегралданады. Клеро теңдеуінің жалпы шешімі: y=Cx+f(С) (*) түріндегі түзулер үйірі, мұндағы С - кез келген тұрақты. Клеро теңдеуінің мұндай жалпы шешімінен басқа: x=-f '(p), y=-pf(p) +f (p) түріндегі ерекше шешімі де болады (мұндағы p - параметр) және ол (*) түзулер үйірінің орауышы болып есептеледі. Клеро теңдеуі - Лагранж теңдеуінің дербес түрі.