Процестердің ұқсастық түрлері

Презентация қосу

.

Тақырып:Өлшемдерді талдау

ОРЫНДАҒАН:ЕРЛАН СЕРІК
ҚАБЫЛДАҒАН:АЙШАБИБІ ДҮЙСЕНБЕКҚЫЗЫ
Жоспар:

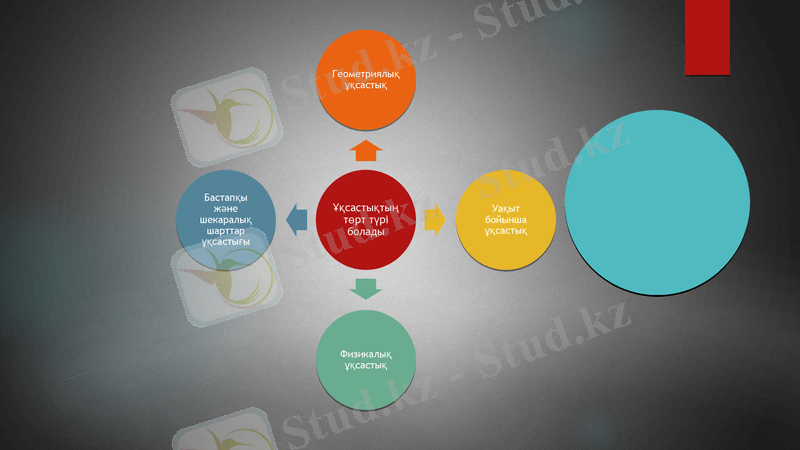
1. Процестердің ұқсастық түрлері. Толық ұқсастық.
2. Ұқсастық теоремалары және оларды
модельдеуде қолдану.
3. Өлшем бірліктерді талдау әдісі.

4.Бақылау сұрақтары
5. Қорытынды
6. Қолданылған әдебиеттер тізімі
1. Процестердің ұқсастық
түрлері. Толық ұқсастық.
Ұқсастық теория жәрдемімен өте күрделі процестерді өндірістік аппараттарда
емес, өлшемі одан да көп кіші моделді аппараттарда және іс жүзінде
қолданылатын тез тұтанғыш немесе денсаулыққа зиянды заттар орнына
моделді заттар пайдаланып зертттеуге болады.
Сондықтан, ұқсастық теория тәсілдері процестерді масштабтандыру мен
моделдеудің негізі болып табылады.
Геометриялы
қ ұқсастық

Бастапқы
және Ұқсастықты Уақыт
шекаралық ң төрт түрі бойынша
шарттар болады ұқсастық
ұқсастығы

Физикалық
ұқсастық
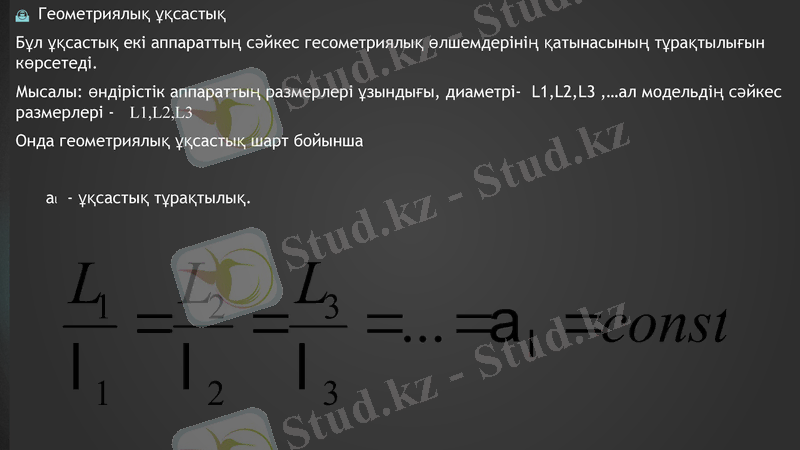
Геометриялық ұқсастық
Бұл ұқсастық екі аппараттың сәйкес гесометриялық өлшемдерінің қатынасының
тұрақтылығын көрсетеді.
Мысалы: өндірістік аппараттың размерлері ұзындығы, диаметрі- L1,L2,L3 ,…ал
модельдің сәйкес размерлері - L1,L2,L3
Онда геометриялық ұқсастық шарт бойынша

al - ұқсастық тұрақтылық.

L1 L2 L3
... соnst
1 2 3
Егер жүйелер қозғалыста болса, онда олардың барлық сәйкес
нүктелері геометриялық ұқсас траекториялармен қозғалуы керек.
Процестердің ұқсастығына аппараттардың геометриялық шарты
орындалуы қажет, бірақ жеткіліксіз.
Уақыт бойынша ұқсастық
Геометриялық ұқсас болған жүйелердің сәйкес нүктелері
геометриялық ұқсас траекториямен уақыт бірлігінде геометриялық
ұқсас жолмен қозғалады. Бұл уақыт бірлігінің бір-біріне қатынасы
тұрақты болады.

Мұнда Т1, Т2, Т3
өндірістік және моделді аппараттардағы уақыт бірліктері, ұқсастық
тұрақтылық
Уақыт бойынша ұқсастық гомохрондық /уақыт бойынша біркелкілік/ -деп
атайды
Физикалық ұқсастық

Қарастырылған екі жүйелердің геометриялық және уақыт бойынша
ұқсастық шарттары орындалған жағдайда ұқсас сәйкес нүктелеріндегі
физикалық тұрақтылықтарының мысалы, тұтқырлық, тығыздық
қатынастары тұрақты болады, яғни
U және u - өндірістік және моделді процестердегі физикалық
тұрақтылықтары.
Бастапқы және шекаралық
шарттар ұқсастығы
Егер геометриялық уақыт бойынша және физикалық ұқсастықтар
жүйелердің алғашқы және шекаралық шарттарына тән болса, онда
олардың бастапқы мысалы температура, қысым және шекарадағы
мысалы, құбыр қабырғасының жанындағы жылдамдық жағдайларға
ұқсас болады.
2.Ұқсастық теоремалары және
оларды модельдеуде қолдану
Ұқсастық инварианттар және
сандар, критерийлер.
Егер бір жүйедегі, мысалы, өндірістік аппаратта сәйкес шамалардың
қатынасын алсақ, онда олардың да қатынасы тұрақты және өлшемсіз
болады, яғни

Өлшемсіз i саны ұқсастық инварианты –деп атайды және былай
жазылады. i = idem соның өзі.
Екі біртекті физикалық шамалардың қатынасын өрнектейтін ұқсастық
инвариатың ұқсастық теорияда симплекс -деп атайды.
Мысалы геометриялық симплекс.
Ұқсастық инварианттар күрделі әртекті шамалардың қатынастары арқылы
да өрнектеледі. Мұндай инварианттарды ұқсастық сандар критерийлер деп
атайды.
Ұқсастық сандардың диференциалдық теңдеулердің бір жағындағы
мүшелерін екінші жағындағы мүшелеріне бөліп, ондағы математикалық
символдарды мысалы, дифференциалды сызып тастап және dx, dy, dz -
мәндерін ұзындықпен /L/ белгілеп табады. Мысалы, Ньютонның екінші заңы
бойынша, денеге әсер ететін күш, оның массасы мен үдеуінің көбейтіндісіне
тең.
Бірінші теорема: Ньютон-Бертран теоремасы деп аталып, былай
дейді: Бір-біріне ұқсас процестер құбылыстар бірдей ұқсастық
сандармен сипатталады және олардың ұқсастық индикаторы бірге тең
болады. Мысалы, Ньютонның екінші заңына бағынатын екі жүйені
өндірістік және моделді қарастырайық.
Бірінші жүйе үшін:

Екінші жүйе үшін:
Бірінші теорема: тәжірбие кезінде қандай шамаларды өлшеу керек
екендігін көрсетеді.
Екінші теорема: Бэкингем-Федерман теоремасы деп аталып, былай
дейді:
Процесске әсер ететін шамалардың байланысынан құрылған
дифференциалдық теңдеудің шешімін, осы шамалардың түзілген
өлшемсіз комплекстердің, яғни ұқсастық сандардың арасындағы
байланыс арқылы өрнектеуге болады.
Мысалы, сұйық немесе газдың құбыр мен қозғалысында берілген
бастапқы және шекаралық шарттар құбырдың диаметрі мен ұзындығы;
ағынның физикалық қасиеттері-тығыздығымен тұтқырлығы;
жылдамдықтың құбырға кірердегі және құбырдың қабырға жанындағы
таралуы ағынның кез келген нүктесіндегі жылдамдықты және екі нүкте
арасындағы қысымдар айырмасын анықтайды.
Үшінші теорема. Кирпечев-Гухман теоремасы – деп аталып,
бірінші теоремаға кері болады:
Бірдей дифференциалдық теңдеулер системасымен
өрнектелетін және бірмәнділік шарттарының ұқсастығы
сақталатын құбылыстар процестер ұқсас болады. Процестерді
өрнектейтін дифференциалдық теңдеулер бірдей болғанда
бірмәнділік шарттардың ұқсастығы анықтаушы сандардың
теңдігінде болады.
Демек, үшінші теореманы былай тұжырымдауға болады: Егер
анықтаушы сандар критерийлер бір біріне сан жағынан тең
болса, онда мұндай құбылыстар процестер ұқсас болады
3.Өлшем бірліктерді талдау әдісі.
Ұқсастық теориясы тәсілдерін процестер дифференциялдық теңдеулер мен өрнектелуі мүмкін
кезде ғана қолдануға болады. Бірақ, өте күрделі процестерді зерттеген кезде, көбінесе, олардың
дифференциалдық теңдеулермен өрнектеу мүмкін емес. Осындай процестерді зерттегенде
оларды өрнектейтін санды (критерийлі) теңдеулер алу үшін өлшем бірліктерін талдау тәсілін
қолданады.
Процесті алдынала тәжірбие нәтижесінде зерттегенде, оған процеске қандай физикалық
шамалардың әсер ететіндігін және олар қандай өлшемдермен өлшенетіндігі белгілі болса ғана,
бұл тәсілді қолдануға болады.
Бұл тәсілдін негізгі Бекингемнің -теоремасы болып табылады: Егер процесті (құбылысты)
сипаттайтын жалпы функциялық байланыс n физикалық өлшемді шамалармен (мысалы,
жылдамдық, тығыздық, тұтқырлық және т.б.) өрнектелсе және бұл шамалар m негізгі өлшем
бірліктерімен (мысалы, масса, ұзындық, уақыт) өлшенсе, онда мұндай функциялық байланыс –
осы шамалардан түзілген (n-m) ұқсастық саны (критерийі) бар санды (критерийлі) теңдеумен
өрнектеледі.
Мысалы, нақты (тұтқыр) сұйықтың қалыптасқан қозғалысын қарастырайық. Мұндай қозғалыста
құбырдың бастапқы және соңғы нүктелеріндегі қысымдар айырмасы (р), құбырдың диаметрі (d)
мен ұзындығы (l), сұйықтың тығыздығы ( ), тұтқырлығы ( ), жылдамдығы (w) және еркін түсу
үдеуі (g) әсер етеді.
Бақылау сұрақтары

Ұқсастық теориясы дегеніміз не?
Қандай процестер ұқсас болады?
Екі ұқсас процестердің арасындағы функциональды байланыс
қандай?
Ұқсастықтар теориясында қандай теоремалар кездеседі және осы
теоремалар көмегімен қандай сұрақтарды шешуге болады?
Ұқсас моделдер қайдан пайда болады және ненің негізінде модельдер
масштабы таңдап алынады?
Қандай ұқсастық критерилері және қандай есептерде қолданылады?
Қорытынды

Қорыта келгенде өлшемдер анализінің тәсілі бойынша, процестерді
өрнектейтін санды (критерийлі) теңдеуді шығарып алу үшін процеске
әсер ететін шамалар саны және олардың бірлік өлшемдері белгілі
болса болғаны. Тәжірибе арқылы процестерді зерттеуде бұл тәсілдің
маңызы күшті.
. Қолданылған әдебиеттер тізімі

1.Беккер М.Е., Лиепиньш Г.К.. Райпулис Е.П. Биотехнология. .1990, 368 с.
.net/Biologiya/
Назарларыңызға
рахмет!!!

Ұқсас жұмыстар

САЯСИ МӘДЕНИЕТ ҚҰРЫЛЫМЫ

Макроэвалюция,жолдары:конвергенция,параллелизм.Бұл процестердің биологиялық маңызы

Деректерді тікелей пайдалану немесе деректерді сақтау

Дискреттік сигналдар

Ес туралы жалпы түсініктер

Саяси мәдениеттің түсінігі, саяси мәдениеттің типологиясы

Қайта жаңғырту

Зейіннің түрлері

Үшбұрыштардың ұқсастығы

Гидродинамикалық ұқсастық. Сұйықтың қозғалыс режимдері

Пәндер