Графтар теориясының элементтері

Графтар. Графтар теориясының элементтері. Сәйкестік, түрлері және қасиеттері

Тексерген: Тазабекова А. С.

Орындаған: Нурлан А. Н.

1 курс 3 жылдық

Граф ұғымы

G=(M, R) алгебралық жүйе граф деп аталады. Мұндағы М-жиынтығы бос емес жиын, оның элементтері графтың төбелері деп аталады, ал бинарлы R қатынасының R M2 элементтері доғалар деп аталады. Сонымен граф төбелері дегеніміз -айналамызды қоршаған ортаның кез келген объектісі. Олардың саны шектеулі болғандықтан, біз оларды натурал сандармен белгілейміз. Ал граф қабырғалары оның кейбір төбелерін қосады. Граф қабырғаларын әдетте латын әріптерімен белгілейді. G= ‹M, R› графының геометриялық кескіні жазықтықта графтың әр төбесін нүкте арқылы белгілеп, егер (a, b) R болса а төбесінен b төбесіне доға жүргізу арқылы алынады.

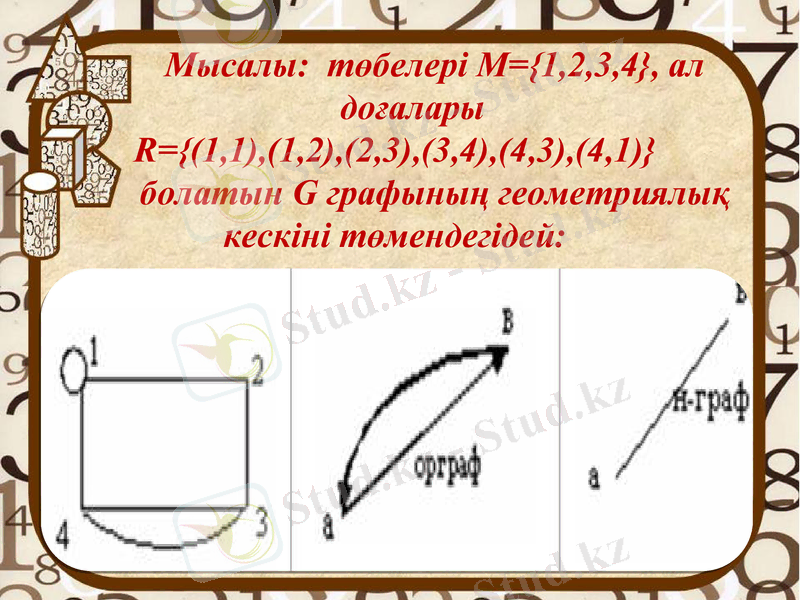
Мысалы: төбелері М={1, 2, 3, 4}, ал доғалары R={(1, 1), (1, 2), (2, 3), (3, 4), (4, 3), (4, 1) } болатын G графының геометриялық кескіні төмендегідей:

Графтың төбелерінің қандай сызықтарымен қосылатындығы (түзу әлде қисық), сызықтардың ұзындығы туралы ақпараттар маңызды емес. Төбелердің арасында байланыс бар екендігі және ол байланыс туралы ақпарат R доғалар жиынында екендігі болса болды. Төбелерді қосатын сызықтардың бағыты көрсетілген болуы мүмкін (мысалдағы сияқты) . Мұндай граф бағытталған граф деп аталады (оргграф) . Оған математикалық түрде мынандай анықтама беруге болады. Анықтама: Егер R қатынасы симметриялы болмаса, яғни (a, b) R, (b, а) R онда G= графы бағытталған (оргграф) деп аталады, ал R қатынасы симметриялы болса (a, b) R, (b, а) R онда G бағытталмаған (неоргграф) немесе н-граф деп аталады Айталық: a, b-граф төбелері, e=(a, b) оларды қосатын доға болсын. Мұндай жағдайда а, b төбелері мен е доғасы инцидентті деп аталады. b мен e доғасы даинцидентті. Әр доға e E өзі қосатын екі төбеге инцидентті болады. Бір доғамен қосылатын 2 төбе сыбайлас ( бүйірлес) деп аталады.

Графтар теориясы-шектеулі математиканың кейбір мәселелерді шешуге геометриялық тұрғыдан келу тән бюолып табылатын бөлім. Граф теориясының негізгі мазмұны графтарды зерттеу болып табылады. Граф - «граф» - «жазамын» деген мағанадағы грек сөзінен алынған.

Жазықтықта әртүрлі бес A, B, C, D, E нүктелерін белгілейік. Осы нүктелерді графтың төбелері, ал оларды қосатын сызықтарды \түзу немесе қисық\ графтың қабырғалары деа атайды.

Бұл графты A, B, C, D, E нүктелерін қосатын сызықтар осы нүктелерден басқа ешбір нүктелерден

қиылыспайтындай етіп те кескіндеуге болады. Қабырғалары тек төбелерінде ғана

қиылысатын графты жазық граф деп атайды.

Графтың мынадай негізгі қасиеттері болады:

Графтардың түрлері

Көптеген қолданбалы есептерде айналамызды қоршаған ортаның әртүрлі объектілер арасындағы байланыстар жүйесі зерттеледі. Объектілер төбелер деп аталып, нүктелер арқылы белгіленеді, ал төбелер арасындағы байланыстар доғалар деп аталып, сәйкес нүктелерді қосатын бағытталған түзулермен белгіленеді. Қала көшелерін граф арқылы кескіндеуге болады: көше қиылысуларын графтардың төбесі деп, ал көшелерді доғалар деп алуға болады; Блок-схемаларды да граф түрінде кескіндеуге болады: блоктар - граф төбелері, ал операцияның орындалу кезегін көрсететін стрелкалар доғалар.