Жоғары дәрежелі теңдеулерді шешу

Презентация қосу

Жоғары дәрежелі теңдеулерді шешу

Орындаған: Жумабаева Айдана
Безу теоремасы
Безу теоремасы P(x) көпмүшелігін x-a екі мүшелікке
бөлгендегі қалдық P(a)-ға тең деп тұжырымдайды.
Көпмүшелік коэффициенттері белгілі бір коммутативті
бірлігі бар сақинада (мысалы, нақты сандар немесе
комплекс сандар өрісінде) жатыр деп саналады.
Дәлелдеу
P(x) көпмүшелігін қалдықпен x-a көпмүшелігіне
бөлейік:
P(x)=( x-a)Q(x)+R(x).
degR(x) аспайтын көпмүшелік. x=a дегенді қойып,( a -a) Q( a)
=0 болғандықтан P(a)=R(a) екендігін табамыз.
Салдар:
а саны сонда тек сонда, егер р(х) қалдықсыз х-а–ға
бөлінсе р(х) көпмүшелігінің түбірі болады (осыдан
Р(х) көпмүшелігінің түбірлер жиыны сәйкес Р(х)
=0 теңдеуінің шешімдер жиынымен бірдей).
Бүтін коэффициентті көпмүшеліктің бос мүшесі
көпмүшеліктің кез келген бүтін түбіріне қалдықсыз
бөлінеді (егер жоғарғ коэффициентті 1 болса, онда
барлық рационал түбірлері де бүтін болады).
а –бүтін коэффициентті А(х) келтірілген
көпмүшеліктің бүтін түбірі болсын. Онда кез
келген бүтін к саны үшін А(к) саны а-к санына
бөлінеді.
1-әдіс. Безу теоремасына сүйеніп,
теңдеудің дәрежесін біртіндеп төмендету

Бұл әдіс теңдеудің рационал, дербес жағдайда бүтін,
түбірлері бар болған жағдайда қолайлы болып табылады. Оның
мәні теңдеудің сол жақ бөлігіндегі көпмүшені рационал
түбірлері арқылы көбейткіштерге жіктеу.
1-мысал.
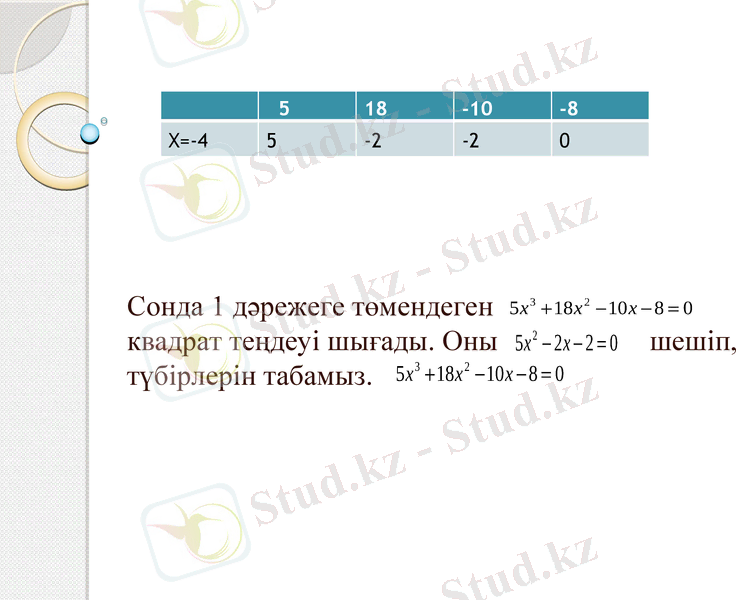
Шешуі: 1-ші салдарға сүйеніп, егер бар болса, бос мүше
бөлгіштері: ±1; ±2; ±4; ±8 сандары ішінен бүтін түбірлерін
іздейміз. х=-4 түбірі болатынына көз жеткізуге болады. Горнер
схемасын пайдаланып теңдеудің сол жақ бөлігіндегі көпмүшені
х+4 екімүшеге бөлеміз.
5 18 -10 -8
X=-4 5 -2 -2 0

Сонда 1 дәрежеге төмендеген
квадрат теңдеуі шығады. Оны шешіп,
түбірлерін табамыз.
2-мысал.
Шешуі: 2-ші салдарға сүйеніп
келтірілген бүтін коэффициентті
теңдеудің бүтін түбірлері бар болса,
бос мүше бөлгіштері ішінен іздейміз.
Тексеру х=2 саны түбір болатынын
көрсетеді. Горнер схемасын
пайдаланып теңдеудің сол жақ
бөлігіндегі көпмүшені х-2 екімүшеге
бөлеміз.
2-әдіс. Топтау арқылы көбейткіштерге жіктеу.

2-мысал.
Шешуі: Қосылғыштардың алғашқы екеуі мен
соңғы екеуін топтап, ортақ көбейткіштерін
жақша сыртына шығара отырып,
көбейткіштерге жіктейміз. Сонда ,
бұдан , яғни теңдеуін
аламыз.
Мұндағы өрнегі х-тің кез келген
мәндері үшін оң мәнге ие болғандықтан,
теңдеуін шешсе жеткілікті.
3-мысал
Шешуі: Әрбір екі қосылғыштан ретімен
топтай отырып, көбейткіштерге жіктейміз.
Сонда
Бұдан бұдан
теңдеуін аламыз. Бұл теңдеу
теңдеулер
жиынымен мәндес.Оларды шешіп
түбірлерін
табамыз.
3-әдіс. Жаңа айнымалы енгізу әдісі.

4-мысал.
Шешуі: белгілеуін енгіземіз.Сонда
теңдеуін аламыз.
формуласын пайдаланып
теңдеуін аламыз.
Осыдан теңдеулер жиынын
аламыз. Біріншісінің шешімі жоқ, екіншісінің
шешімі . Белгілеудегі орнына қойсақ,
немесе . Бұл теңдеулерді
шешіп, түбірлерін табамыз.
Назарларыңызға рахмет

Ұқсас жұмыстар

Жоғары дәрежелі теңдеулер

Жұп коэффициенті бар теңдеуді шешу

Иррационал теңдеулерді шешу

Квадрат теңдеулерді шешудің әр түрлі тәсілдері

Теңдеулер жүйесін шешу

Мектеп математикасындағы квадраттық теңдеулерді шешу жолдары

Логарифмдік теңдеулерді шешу туралы ақпарат

Толымсыз квадрат теңдеулерді шешу

Иррационал теңдеулер

Айнымалы коэффициенттерімен дербес туындылы дифференциалдық теңдеулерді математикалық Maple пакеттерінде зерттеу және келтіру

Пәндер