Екінші дәуір - Евклидтен Декартқа дейінгі кезең

Презентация қосу

ГЕОМЕТРИЯЛЫҚ
ТЕРМИНДЕРДІҢ
ПАЙДА БОЛУЫ.
S
S

А В
«Геометрия» атауы дәл аударғанда «жер өлшеу»
болады. Бұл ғылымның алғашқы нышандары
Ежелгі Мысыр (Египет) елінде шыққан. «Жер
учаскелерін өлшеу нәтижесінде,— деп жазған б. з. б.
4 ғ-да өмір сүрген грек математигі Евдем,—
мысырлықтар геометрия шлымын шығарды». Жер
өлшеу өнерін мысырлықтардан үйренген ежелгі
гректер оны алғашқы кезде өз тілінде «Геометрия»
деп атаған. Осы сөз кейін көптеген халықтардың
тіліне еніп, ғылыми термин болып кеткен
Фигуралар кеңістік формалары болып
табылады.

Геометрия ұғымдары дүниеде
кездесетін заттардың дербес физикалық
қасиеттерін еске алмай, абстракциялап,
яғни дерексіздендіріп, олардың тек
мөлшері мен өзара жайғасуын ғана
қарастыру нәтижесінде пайда болған.
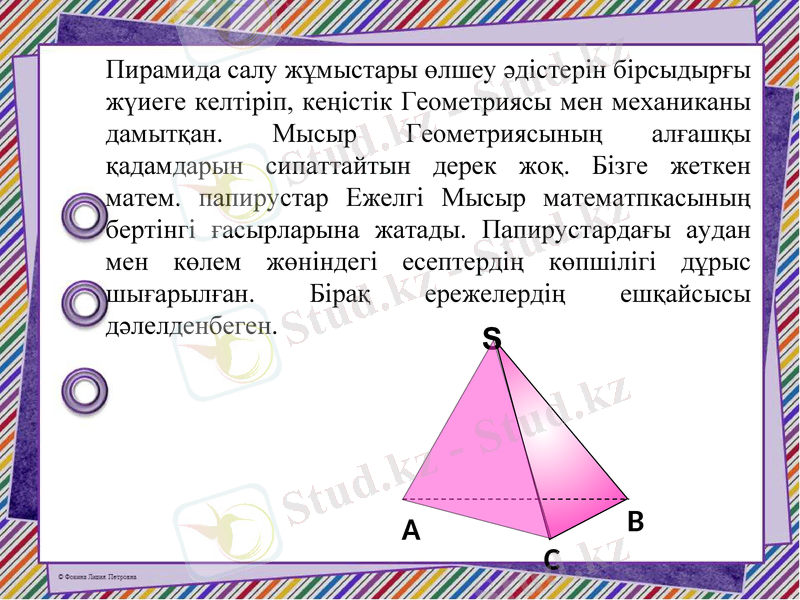
Пирамида салу жұмыстары өлшеу әдістерін
бірсыдырғы жүиеге келтіріп, кеңістік Геометриясы мен
механиканы дамытқан. Мысыр Геометриясының
алғашқы қадамдарын сипаттайтын дерек жоқ. Бізге
жеткен матем. папирустар Ежелгі Мысыр
математпкасының бертінгі ғасырларына жатады.
Папирустардағы аудан мен көлем жөніндегі есептердің
көпшілігі дұрыс шығарылған. Бірақ ережелердің
ешқайсысы дәлелденбеген. S
S

А В
С
Үшбұрыштың, трапецияның, дөңгелектің
ауданы жуық түрде есептелген, табандары
квадрат болып келген қиық пирамиданың
көлемі дәл табылған. Ежелгі Вавилон
Геометриясының деректері балшықтан иленіп
жасалған тақташаларға жазылып қалған.
Оларға қарағанда ұзындық, аудан, көлем
жөніндегі мысырлықтар білген есептерді
вавилондықтар да шығара білген.
Вавилондықтар кейбір дұрыс көпбұрыштарды,
қиық конусты т. б. қарастырған, шеңберді 360
градусқа бөлуді шығарған, есептерді
теңдеулерге келтіруге машық болған,
Геометрияны астрономияға қолдана
бастаған. Вавилондықтар Пифагор
теоремасын да білген. Азын-аулақ геом.
білімдер Ежелгі Үндістан мен Қытайда да
болған. Б. з. б. 7—0 ғ-да сол кездегі әлеуметтік
жағдаилар дүн. жүз. тарих сахнасына Ежелгі
Грецияны шығарды.
Мысалы, радиусы r дөңгелектің ауданын
мысырлықтар 256 r2 : 81 деп, вавилондықтар З r2 деп
есептеген. Осылардың дұрысын таңдап алу үшін
тиісті сөйлемді — теореманы дәлелдеу керек болды.
Бірталай теоремаларды Фалес, Пифагор, Гипократ,
Демокрит дәлелдеді. Дәлелдемелердің дұрыс
қалыптасуына философия ғылымының да ықпалы
болды. Сөйтіп, б. з. б. 5 ғасырда геометрия өзіне тән
ұғымдары мен әдістері бар жүйелі ғылым дәрежесіне
көтерілді.
Осы дәуірдің аяғында Гиппократ, Феодоспй
т. б. Геометрия негіздері» деген атпен көлемді
кітаптар жазды. Екінші дәуірдің басы болған
Евклид еңбектері шыққанда бұл кітаптар кеиін
ысырылып, акыры мүлде ескерусіз қалып
қойды. Олардың ешқайсысы сақталмаған.
Екінші дәуір — Евклидтен Декартқа дейінгі кезең; ол
2000 жылға созылды. Ұлы грек математигі Евклид
Геометрияның өзіне дейінгі табыстарын жинап, талдап,
қорытып, бір ізге түсіріп, б. з. б. 300 ж. шамасында
«Негіздер» атты, 13 бөлімнен құралған, Шығарма жазды
(қ. Евклид «Негіздері»).
Онда геометрия аксиомалар мен
постулаттар негізінде логикалық жолмен
кұрылған жүйелі дедуктивтік ғылым
(кеңістіктің формалары мен
қатынастары туралы ғылым)
дәрежесінде баяндалды «Негіздерде»
121 анықтама, 5 постулат, 9 аксиома, 373
теорема келтірлген.
Осы күнгі элементар геометрия, жалпы алғанда,
Евклид қалыбынан шыққан (қ. Евклид).
Геометрияға Архимед пен Аполлоний ірі үлес
қосты бұлардың біріншісі дөңгелектің, парабола
сегментінің ауданы, пирамиданың, конустың,
шардың көлемі жөніндегі теоремаларды т. с. с.
тағайындады, екіншісі конустық қималарды
мұқият зерттеп, құнды ғылми мұра қалдырды.
Астрономпямен шұғылданған математиктер —
Гиппарх, Птолемей, Менелай т. б. сфералық
Геометрия мен тригонометрияны
қалыптастырды. Евклид, Архимед, Аполлоний
заманы грек Геометриясының «алтын ғасыры»
болды, одан кейін Грецияның ғылымы мен
мәдениеті құлдыраи бастады.
Орта ғасырларда элементар Геометрия
Үндістанда, Орта Азияда, араб елдерінде
дамыды. Орта Азия және Қазақстан
ғалымдарынан Геометриямен
шұғылданғандар: Жауһари, Фараби,
Бозжани, Бируни, Кәши т. б. болды. Екінші
дәуірдің аяғында Геометрия Батыс Европада
жандана бастады. Бұл кезде И. Кеплер мен Б.
Кавальеридің еңбектері тарихи белес болды.
Үшінші дәуір Декарттан Лобачевскийге дейінгі
200 жылды қамтиды. Бұл дәуірде аналитикалық,
проективтік, сызба және дифференциалдық
Геометриялар туды. Аналитикалыц геометрия
координаталар әдісіне сүйенеді, онда нүктенің орны
сандар арқылы, сызықтар мен беттер теңдеулер
арқылы анықталады. Геометрияның бұл саласының
іргесін Р. Декарт пен П. Ферма қалады, А. Клеро
мен Л. Эйлер кемелдендірді. Фигураларды
проекциялар арқылы түрлендіру жолдарын зерттеу
нәтижесінде проективтік Геометрия қалыптасты.
Бұл бағытта Ж. Дезарг, Б. Паскалъ, Ж. Понселе, X.
Штаудт, Я. Штеинер жемісті еңбек етті.
Кеңістіктегі фигураны жазықтықта кескіндеу жолдарын
талдап, Г. Монж сызба Геометрияны жасады. Сызба геометрия
проективтік Геометрияның тарауы болып табылады. Эйлер мен
Монж дифференциалдық есептеу әдістерін Геометрияға қолдана
бастаған болатын. К. Гаусс бұл мәселені одан орі дамытып,
классикалық дифференциалдың геометрияны қалыптастырды.
Дифференциалдық Геометрия сызықтар мен
беттердің қасиеттерін лифференциалдар
бойынша зерттейді. Онда Гаусс көрсеткен
бірінші, екінші, үшінші квадраттық формалар
маңызды роль атқарады. Бұл Геометриялардың
бәрінің де түп негізіне евклидтік геометрия
алынады.
Төртінші дәуір Лобачевский еңбектерінен басталды.
Евклидтің 5-постулатын Лобачевскпй аксиомасымен
ауыстырып, орыс ғалымы жаңа Геометрия жасады. Бұл
Геометрияға К. Гаусс пен Я. Больяй да келді. 5-постулат
орнына Риман аксйомасын алып, Б. Риман эллипстік
Геометрияның негізін салды. Риман кеңістікті кез келген
біртектес объектілер мен құбылыстардың үздіксіз жиыны
ретінде түсіну қажеттігін көрсетті. Бұл идеяның құлашы кең
болды. Соның арқасында кеңістіктің көптеген математикалық
теориялары жасалды. Лобачевскии идеялары Геометрия
негіздемелерінің шығуына, Геометриялардың жалпылануына
және одан әрі дамуына жол ашты.
Қ а з і р г і Геометрия кеңістік пен фигураны жиын ұғымы
арқылы анықтайды. Онда кеңістік әдеттегі қатынастар
іспеттес дәйекті қатынастар тағапындалған элементтердің
(«нүктелердің») жиыны ретінде қарастырылады. Тиісті
қатынастар тағайындалғанда сәуле түстерінің жиыны,
физикалық жүйе күйлерінің жиыны, [0; 1] кесіндісіндегі
үздіксіз функцнялардың жиыны т. с. с. «кеңістіктер»
құрастыра алады. Сәуле түстері, күилер, функциялар сол
сәикес «кеңістіктердің» «нүктелері» рольдерін атқарады.
Негізгі кеңістік қатынастары ретінде «ара қашықтық»,
«іліктестік», «нүкте аймағы», «сәйкестік» т. б. ұғымдар
алынады. Жиындар мен қатынастарды әр түрлі етіп алып, әр
түрлі Геометриялар жасауға болады. Соңғы кезде
өлшемдерінің саны шектеусіз болатын кеңістіктің
Геометриясы қалыптасты. Ол функционалдық анализ
курсында баяндалады.
Метр (фр. metre, гр. metron – өлшем) – бірліктердің
халықаралық жүйесіндегі (СИ) ұзындықтың негізгі өлшем бірлігі.
1960 жылға дейін Метрдің эталоны – ұзындықтың штрихты
өлшемі платина-иридий қоспасынан жасалып, Севр қаласындағы
(Париж қаласының жанындағы) Өлшеуіштер мен таразылар
жөніндегі халықаралық бюрода сақталған білеуше (брусок)
болған. Өлшеуіштер мен таразылар жөніндегі 11-Бас конференция
(1960) Метрдің жаңа анықтамасын қабылдады: “Метр – Криптон-
86 атомының 2р10 және 5d5 деңгейлерінің аралығындағы ауысуы
сәйкес келетін сәуле шығаруының вакуумдағы 1650763,73 толқын
ұзындығына тең ұзындық”. КСРО-да алғашқы эталоны ұзындық
бірлігі – метрді қайта жаңғыртуға және оның өлшемін
ұзындықтың басқа өлшемдеріне таратуда құрамында ұзындықты
дәл өлшеуге арналған интерферометр бар аппаратуралар кешенін
қолданды.
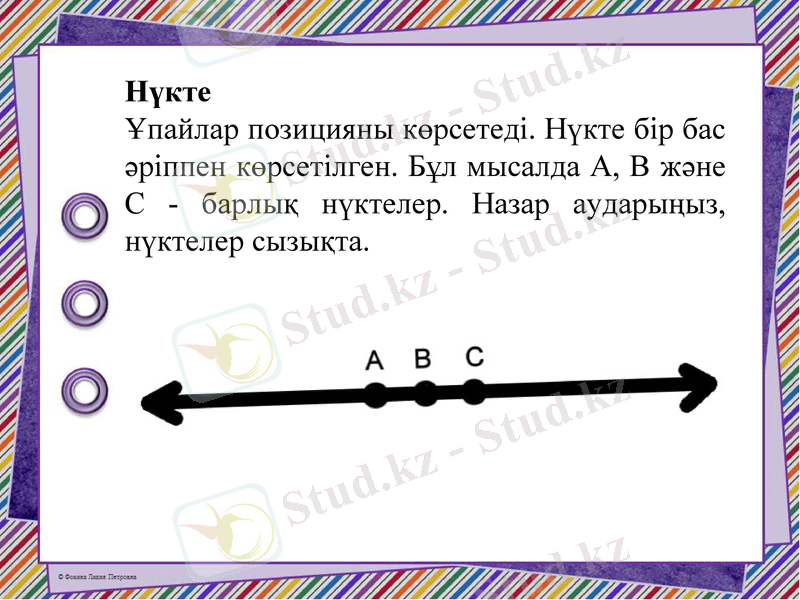
Нүкте
Ұпайлар позицияны көрсетеді. Нүкте бір бас
әріппен көрсетілген. Бұл мысалда A, B және
C - барлық нүктелер. Назар аударыңыз,
нүктелер сызықта.
Сәуле - берілген нүктеден және соңғы нүктенің бір
жағындағы барлық нүктелер жиынтығынан тұратын
сызықтың бөлігі.
Суретте А - соңғы нүкте және бұл сәуле А-дан
басталатын барлық нүктелер сәулеге қосылғанын
білдіреді.
Бұрышты екі сәуле немесе жалпы
соңғы нүктесі бар екі сызық сегменті
ретінде анықтауға болады. Соңғы нүкте
шыңы ретінде белгілі болады. Бұрыш
екі сәуле бірдей нүктеде кездескенде
немесе біріккенде пайда болады.
Тік бұрыш керемет сызықты құрайды.
Деб Рассел. Тік бұрышы 180 градус және
сызық сегменті ретінде пайда болады.
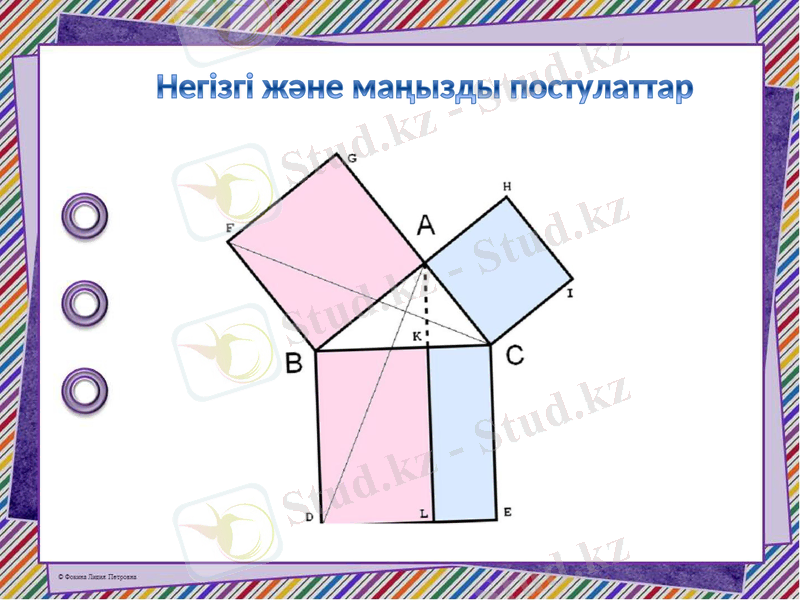
Негізгі және маңызды постулаттар
Александрия Евклиді біздің дәуірімізге дейінгі 300-ге
жуық «Элементтер» деп аталатын 13 кітап жазды. Бұл
кітаптар геометрияның негізін қалады. Төмендегі
постулаттардың кейбірін Евклид өзінің 13 кітабында
келтірген. Олар аксиома ретінде қабылданды, бірақ
дәлелсіз. Евклид постулаттары біраз уақыт аралығында
аздап түзетілді. Кейбіреулері осында аталған және
Евклид геометриясының бөлігі болып қала береді. Бұл
туралы біліңіз. Егер сіз геометрияны түсінгіңіз келсе,
оны оқып, есте сақтаңыз және осы бетті ыңғайлы
сілтеме ретінде сақтаңыз.
Геометрияда білу өте маңызды бірнеше
негізгі фактілер, мәліметтер және
постулаттар бар. Геометрияда бәрі
дәлелденбеген, сондықтан біз кейбіреулерін
қолданамыз постулаттар, олар біз
қабылдайтын негізгі болжамдар немесе
дәлелденбеген жалпы тұжырымдар. Төменде
кіріспе деңгей геометриясына арналған
бірнеше негіздер мен постулаттар
келтірілген. Мұнда айтылғандарға қарағанда
постулаттар көп. Келесі постулаттар
бастаушы геометрияға арналған.
Бұрышта тек бір бисектор болуы мүмкін.
Бисектор - бұл бұрыштың ішкі жағында
орналасқан және сол бұрыштың екі жағы
бірдей тең бұрыш жасайтын сәуле. Рэй АД -
А бұрышының бисекторы.
Планиметрия
Планиметрия (лат. planum — жазықтық және METREO -
"өлшеймін") — элементар геометрияның жазықтықта жатқан
фигуралардың қасиеттерін зерттейтін бөлімі. Әдетте
Планиметрия деп орта мектепте оқылатын геометрия курсының
бір бөлімі түсініледі. Планиметрияның мазмұнын ертедегі грек
ғалымы Евклид айқындаған және оның баяндалу тәсілін
жасаған
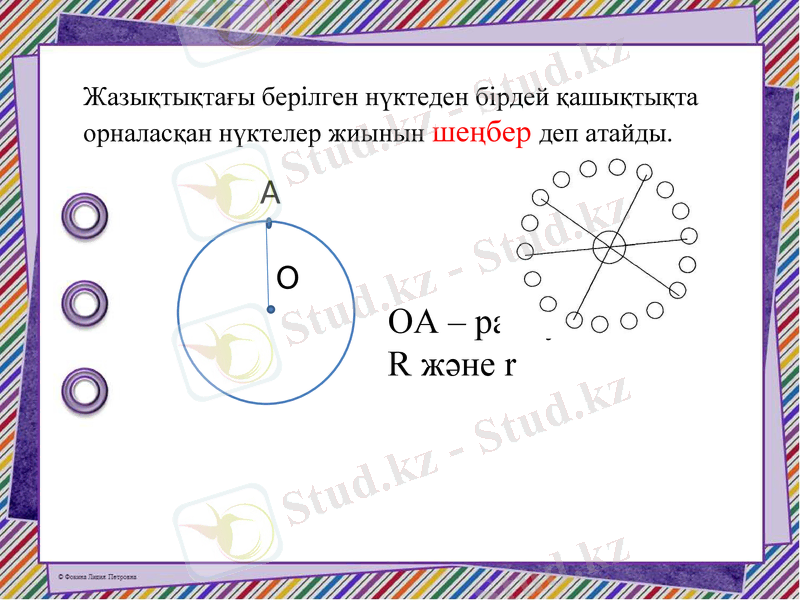
Жазықтықтағы берілген нүктеден бірдей қашықтықта
орналасқан нүктелер жиынын шеңбер деп атайды.

А

О
ОА – радиус
R және r
Радиус (латын тілінде radіus — дөңгелек
шабағы, сәуле) — шеңбердің не сфераның кез
келген нүктесін центрімен қосатын кесінді.
Сондай-ақ осы кесіндінің ұзындығын да
радиус деп атайды.
Хорда (гр. chorde — желі) — өте тығыз, бір-бірімен жанаса
орналасқан көпіршікті клеткалардың жиынтығынан тұратын
серпімді мүше. Ол хордалы жануарлардың арқа жағында ұзына
бойы созылып жатады және ішкі қаңқаның қызметін атқарады.
Хорда ұрық дамуының алғашқы кезеңінде ішектің артқы
тұсынан, алдыңғы шеті тұйық өскін түрінде біртіндеп пайда
болады. Ол эктодермалық ұрық жапырақшасынан түзіледі.
Хордаға жан-жағынан өзара бір-біріне ұқсас бұлшықет бөліктері
бекиді. Хорда мен бұлшықеттер бірігіп, тірек-қимыл аппаратын
құрайды, соның нәтижесінде жануарлар қозғала алады.
Хорданың пішіні цилиндрге ұқсас, оның үстіңгі жағында ұзына
бойы жүйке түтігі орналасады.
Дөңгелек деп шеңбермен шектелген жазықтықтың ішкі
бөлігін айтамыз немесе дөңгелек дегеніміз- жазықтықтың
берілген О нүктесіне дейінгі қашықтықтары берілген R
санынан артпайтын нүктелерінің жиынтығы
rn - үшбұрыштың О төбесінен түсірілген
биіктік (апофема деп атайды)
А1, А2 - шеңберге іштей сызылған
көпбұрыштың қабырғасы, сонда ОА1А2
-үшбұрышының ауданы
О 1
S rn A 1 A 2
формуласымен анықталатындықтан,
O R
А2 n- бұрыштың ауданы
D rn 1
S rn A1 A2 nформуласымен анықталады.
Көпбұрыштың периметрі
болғандықтан, п-шексіз өссе,
A1 A 2 n Pn - ге ұмтылады.
А1 Олай болса, rn R, Pn C 2 R
А3
S n R 2 R R 2
Теорема дәлеледенді.
• Дөңгелек секторы деп доға және дөңгелектің осы доғаға тірелген радиустарымен шектелген бөлігін
айтамыз.

Дөңгелектің ауданы - R
Центрлік бұрышы 1 градусқа тең сектор
ауданы дөңгелек ауданының 1 бөлігіне тең,
сонда: R 360
360
Центрлік бұрышы болатын сектор ауданы
R 2
S сек
360
Егер радиан есебімен берілсе,онда сектор
О ауданы
R 2
S сек
А
В
• Кез келген хорда дөңгелекті екі бөлікке бөледі. Осы
бөліктердің әрқайсысын дөңгелектің сегменті деп
атайды.
• бұрышының шамасына байланысты сегмент
ауданы сәйкес сектор ауданынан АОВ үшбұрышының
ауданын азайту немесе қосу арқылы анықталады.

А В S сег S сек S

А В
0
Егер 180 болса, “-” таңбасы,
ал 1800 болса, “+” таңбасы алынады

R 2
S сег 0
S
360
Қорытынды:
Геометрия табиғатты зерттеуде,
техниканы өркендетуде қуатты құрал
болып табылады. Ол математикалық
анализ, механика, физика, астрономия,
геодезия, картография, кристаллография т.
б. ғылымдарға елеулі әсер етіп отырады.
Пайдаланған әдебиеттер:
•А.Көбесов. Математика тарихы. Алматы.1993.
О.А.Жәутіков. Орыс математикасының атақты
ғалымдары. Алматы. Қазақ мемлекет баспасы .
1956.
• С. Елубаев О.А.Жәутіков. Математиканың даму
тарихы. Алматы. «Мектеп» 1967.

Ұқсас жұмыстар

ҚАЗАҚ ӘДЕБИ ТІЛІНІҢ ҚАЛЫПТАСУЫ,ДАМУ ТАРИХЫ

ЭМПИРИКАЛЫҚ ӘЛЕУМЕТТАНУ

Антикалық мәдениет

Қазақстан тарихын оқытудың мақсаты мен міндеттері және оның басты кезеңдері мен тарихнамасы

ЖЕРГЕ ОРНАЛАСТЫРУ ТАРИХИ КЕЗЕҢДЕРІ

Философияның қалыптасуының негізгі кезеңдері

Қайта өрлеу мәдениеті

Ассирия патшалығы

БИОГЕНДІ КЕЗЕҢ

Эллинизм өнерін бірыңғай тұтас өнер деп қарастыруға болмас

Пәндер