Үшбұрыш және оның негізгі элементтері мен теоремалары




Үшбұрыш деп бір түзудің бойында жатпайтың үш нүктеден және оларды қосатын үш кесіндіден құралатын тұйық геометрикалық фигураны атайды.
Үшбұрыштардың түрлері:
тең қабырғалы
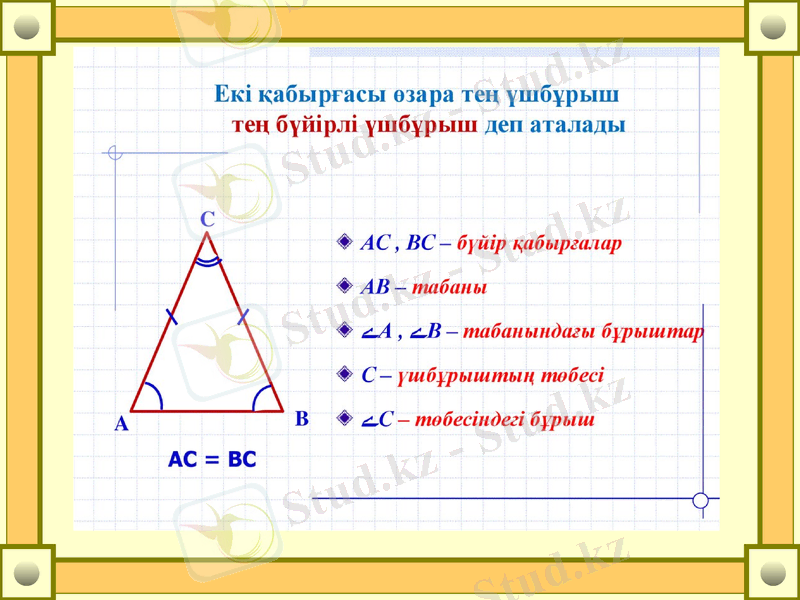
теңбүйірлі
сүйірбұрышты
тік бұрышты
доғал бұрышты.

А
С
В
D
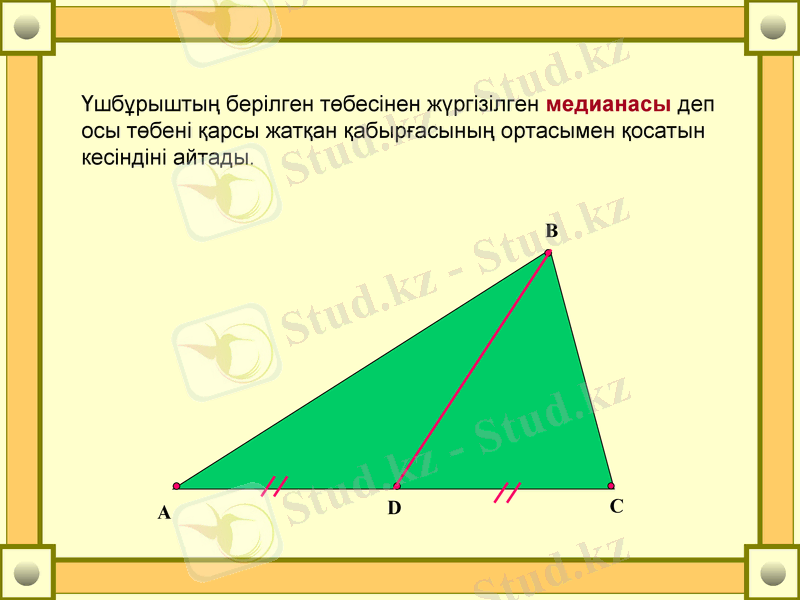
Үшбұрыштың берілген төбесінен жүргізілген медианасы деп осы төбені қарсы жатқан қабырғасының ортасымен қосатын кесіндіні айтады.
А
В
R
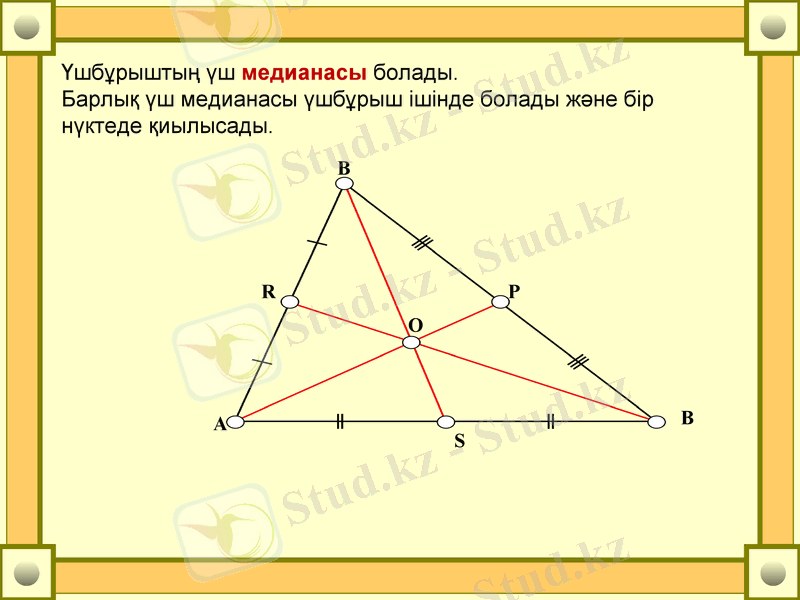
Үшбұрыштың үш медианасы болады.
Барлық үш медианасы үшбұрыш ішінде болады және бір нүктеде қиылысады.
P
S
В
О
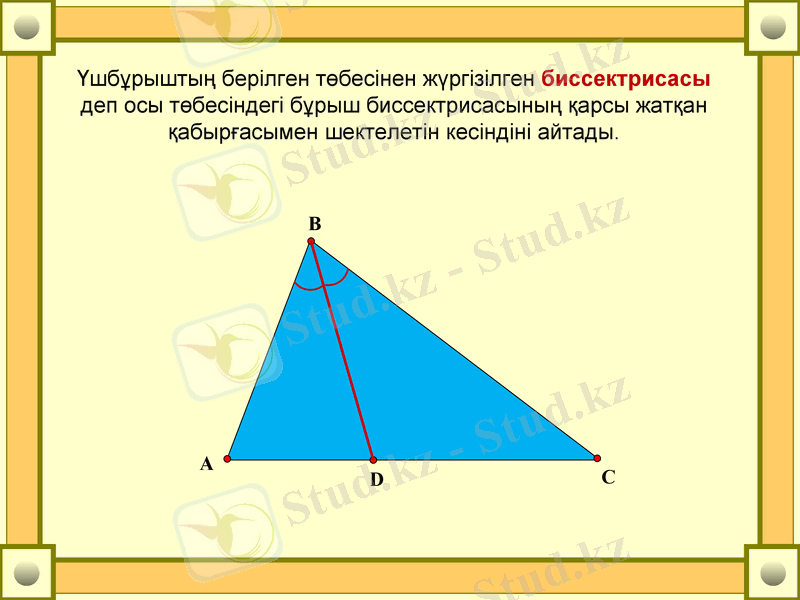
Үшбұрыштың берілген төбесінен жүргізілген биссектрисасы деп осы төбесіндегі бұрыш биссектрисасының қарсы жатқан қабырғасымен шектелетін кесіндіні айтады.
В
А
С
D
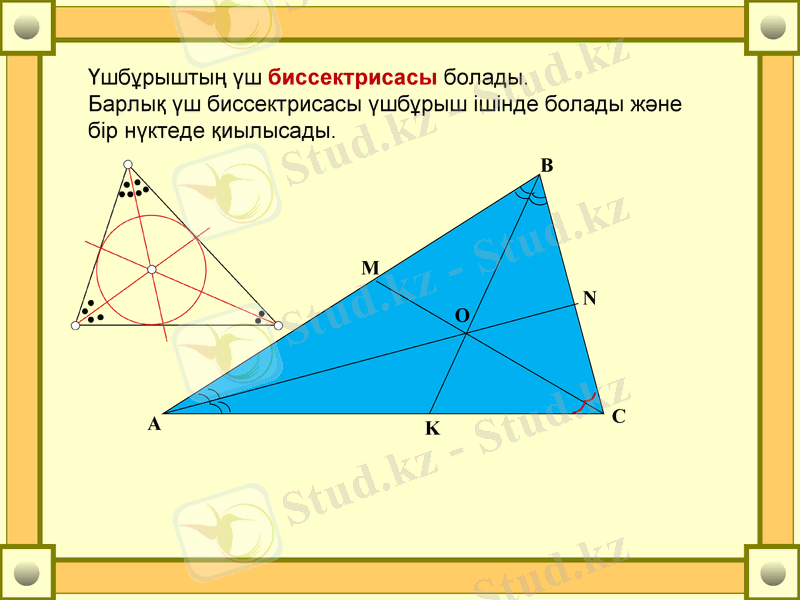
Үшбұрыштың үш биссектрисасы болады.
Барлық үш биссектрисасы үшбұрыш ішінде болады және бір нүктеде қиылысады.
А
О
K
M
С
N
В
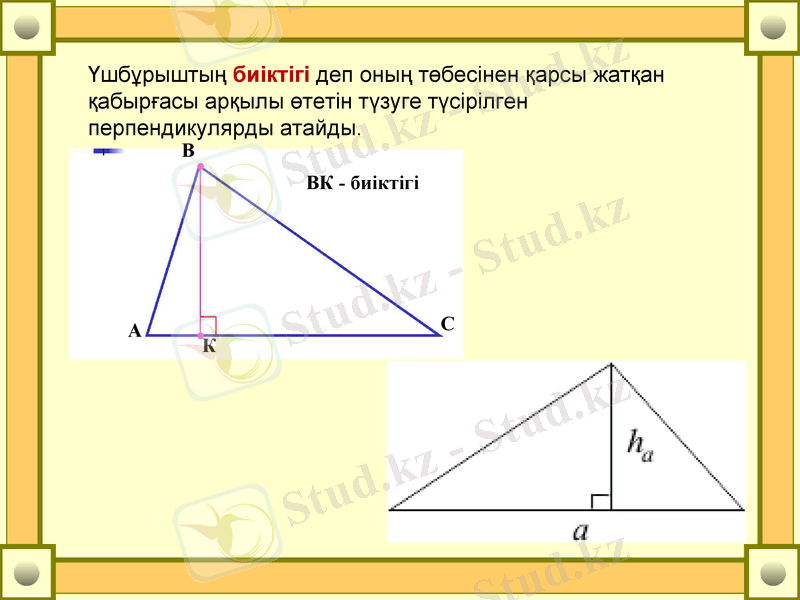
Үшбұрыштың биіктігі деп оның төбесінен қарсы жатқан қабырғасы арқылы өтетін түзуге түсірілген перпендикулярды атайды.
А
С
В
К
ВК - биіктігі
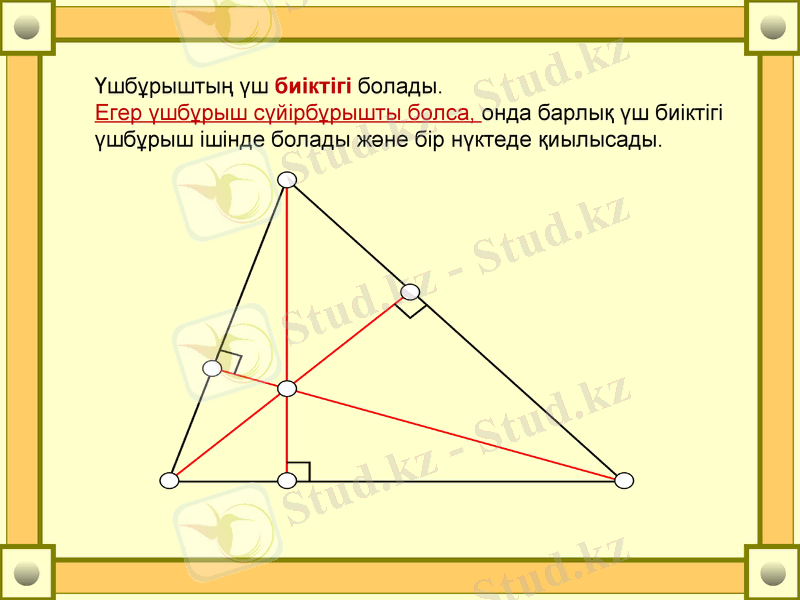
Үшбұрыштың үш биіктігі болады.
Егер үшбұрыш сүйірбұрышты болса, онда барлық үш биіктігі үшбұрыш ішінде болады және бір нүктеде қиылысады.
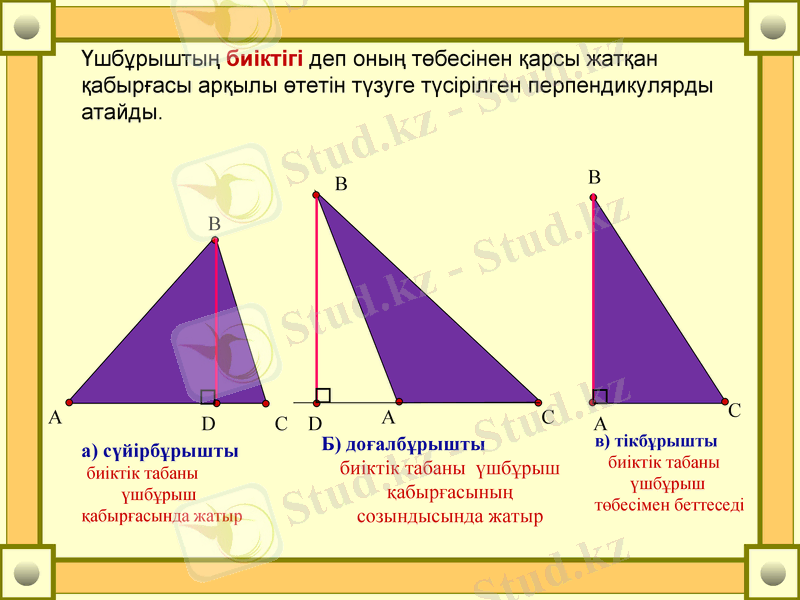
Үшбұрыштың биіктігі деп оның төбесінен қарсы жатқан қабырғасы арқылы өтетін түзуге түсірілген перпендикулярды атайды.
А
А
А
В
В
В
С
С
С
D
D
а) сүйірбұрышты
биіктік табаны
үшбұрыш
қабырғасында жатыр
Б) доғалбұрышты
биіктік табаны үшбұрыш қабырғасының созындысында жатыр
в) тікбұрышты
биіктік табаны
үшбұрыш
төбесімен беттеседі
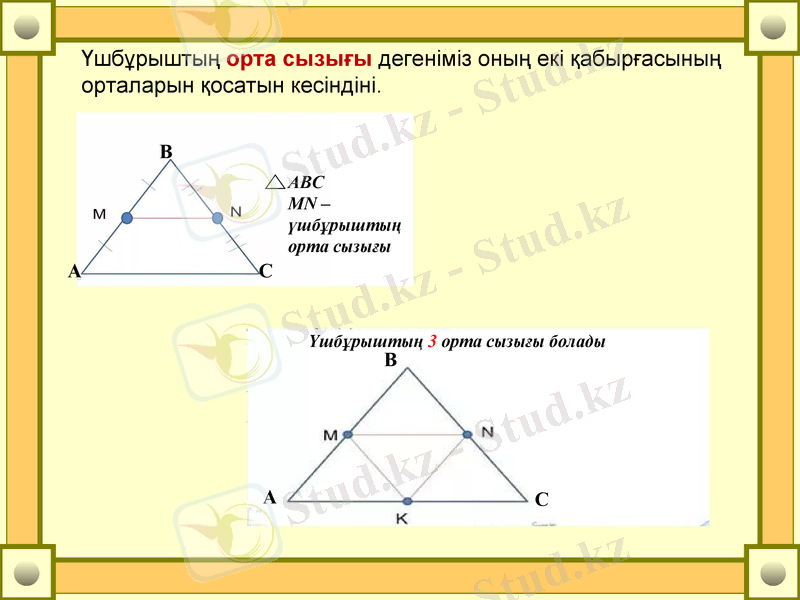
АВС
MN - үшбұрыштың орта сызығы
Үшбұрыштың орта сызығы дегеніміз оның екі қабырғасының орталарын қосатын кесіндіні.
В
А
С
Үшбұрыштың 3 орта сызығы болады
А
С
В

Үшбұрыштардың ұқсастық белгілері
1) Екі бұрышы бойынша - Егер бір үшбұрыштың екі бұрышы екінші үшбұрыштың сәйкес екі бұрышына тең болса, онда мұндай үшбұрыштар ұқсас болады.
2) Екі қабырғасы мен арасындағы бұрышы бойынша - Егер бір үшбұрыштың екі қабырғасы және олардың арасындағы бұрышы, екінші үшбұрыштың сәйкес екі қабырғасына пропорционал және арасындағы бұрышымен тең болса, онда мұндай үшбұрыштар ұқсас болады.
3) Үш қабырғасы бойынша - Егер бір үшбұрыштың үш қабырғасы сәйкес екінші үшбұрыштың үш қабырғасына пропорционал болса, онда бұл үшбұрыштар ұқсас болады.



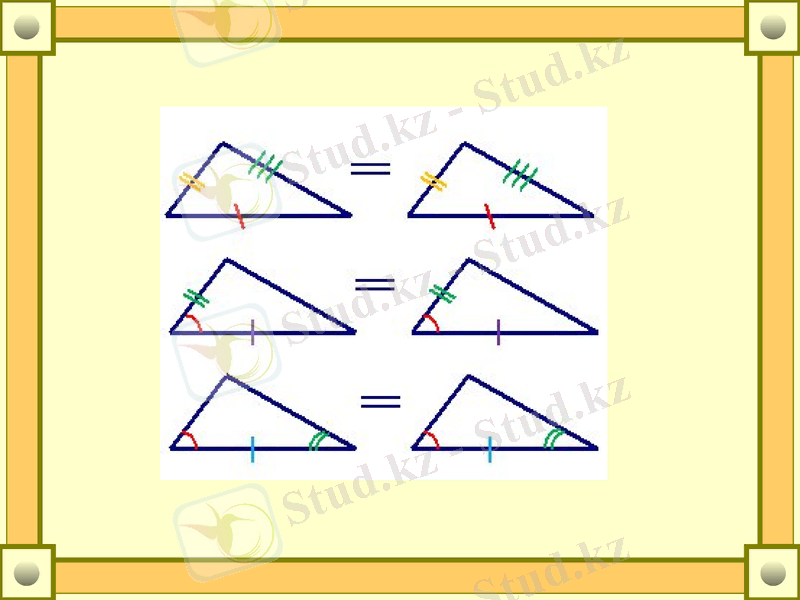
Үшбұрыштың теңдік белгілері
Егер бірінші үшбұрыштың екі қабырғасы мен олардың арасындағы бұрышы екінші үшбұрыштың сәйкес екі қабырғасы мен арасындағы бұрышқа тең болса, онда бұл үшбұрыштар тең болады.
Егер бірінші үшбұрыштың бір қабырғасы және оған іргелес жатқан екі бұрышы екінші үшбұрыштың сәйкес қабырғасы мен оған іргелес жатқан екі бұрышына тең болса, онда бұл үшбұрыштар тең болады.
Егер бір үшбұрыштың үш қабырғасы екінші үшбұрыштың сәйкес үш қабырғасына тең болса, онда бұл үшбұрыштар тең болады.
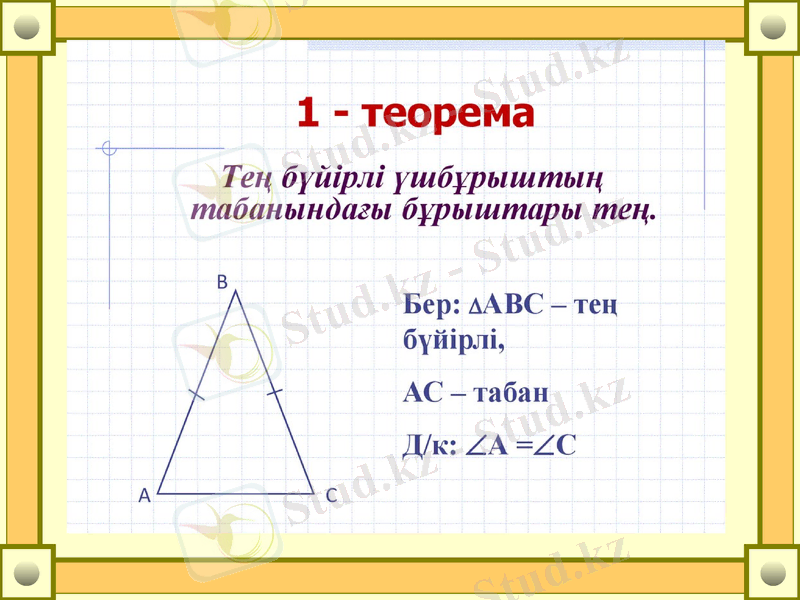
Биссектрисаның қабырғалардан қашықтығы туралы теорема
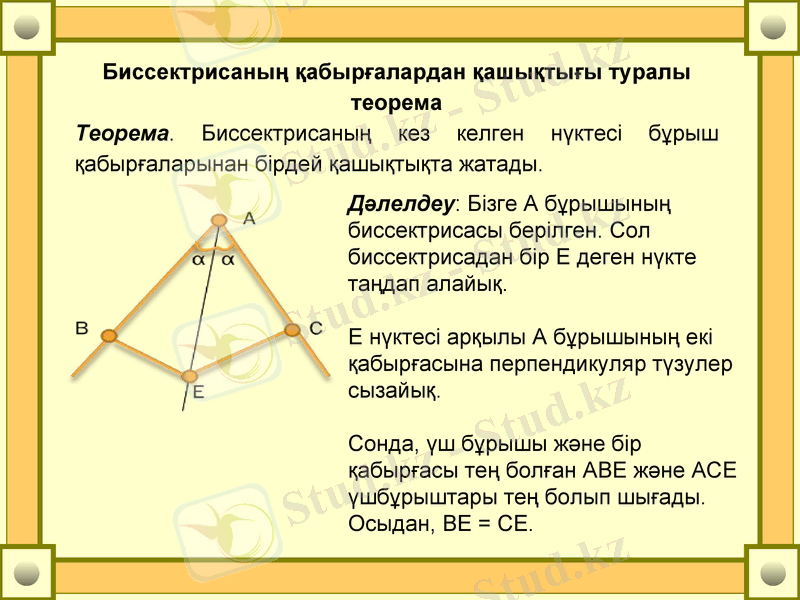
Теорема. Биссектрисаның кез келген нүктесі бұрыш қабырғаларынан бірдей қашықтықта жатады.
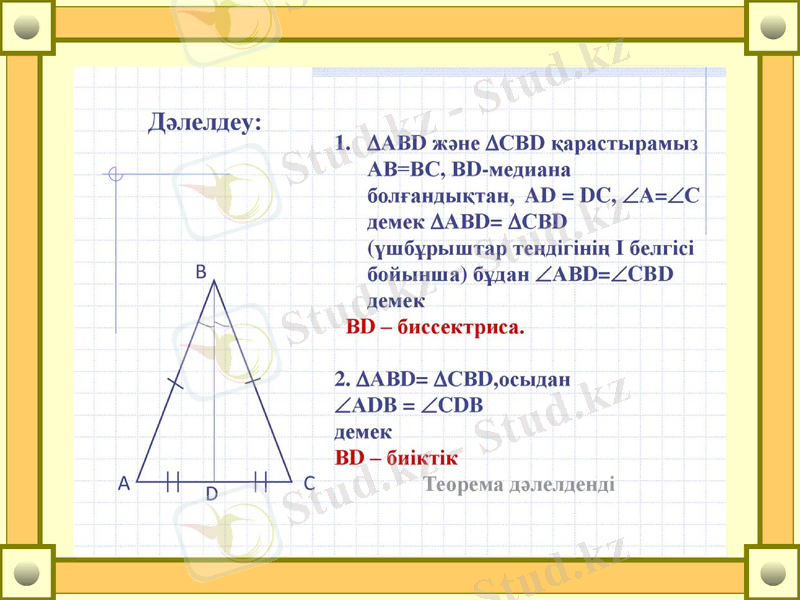
Дәлелдеу: Бізге А бұрышының биссектрисасы берілген. Сол биссектрисадан бір Е деген нүкте таңдап алайық.
Е нүктесі арқылы А бұрышының екі қабырғасына перпендикуляр түзулер сызайық.
Сонда, үш бұрышы және бір қабырғасы тең болған АВЕ және АСЕ үшбұрыштары тең болып шығады. Осыдан, ВЕ = СЕ.
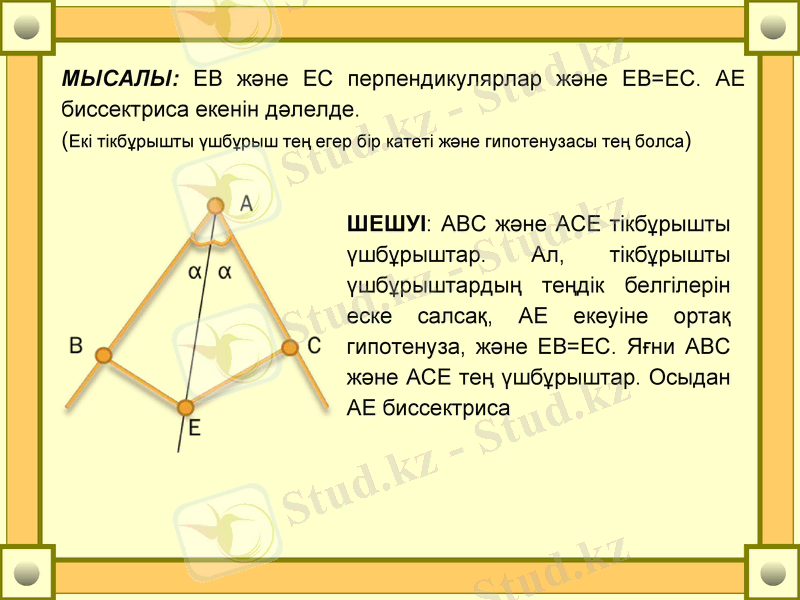
МЫСАЛЫ: ЕВ және ЕС перпендикулярлар және ЕВ=EC. AE биссектриса екенін дәлелде.
(Екі тікбұрышты үшбұрыш тең егер бір катеті және гипотенузасы тең болса)
ШЕШУІ: АВС және АСЕ тікбұрышты үшбұрыштар. Ал, тікбұрышты үшбұрыштардың теңдік белгілерін еске салсақ, АЕ екеуіне ортақ гипотенуза, және ЕВ=EС. Яғни АВС және АСЕ тең үшбұрыштар. Осыдан АЕ биссектриса
Үшбұрыштың биссектрисаларының қиылысу нүктесі
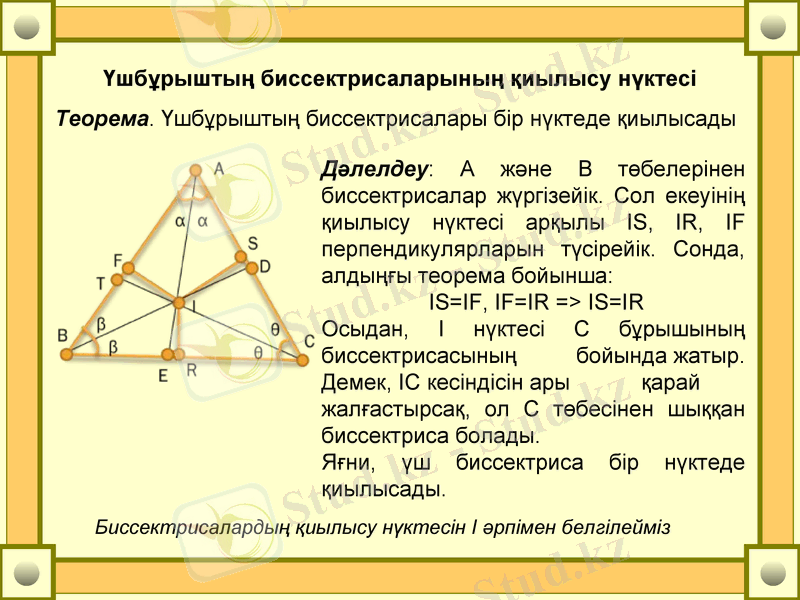
Теорема. Үшбұрыштың биссектрисалары бір нүктеде қиылысады
Дәлелдеу: А және В төбелерінен биссектрисалар жүргізейік. Сол екеуінің қиылысу нүктесі арқылы IS, IR, IF перпендикулярларын түсірейік. Сонда, алдыңғы теорема бойынша:
IS=IF, IF=IR => IS=IR
Осыдан, І нүктесі С бұрышының биссектрисасының бойында жатыр. Демек, ІС кесіндісін ары қарай жалғастырсақ, ол С төбесінен шыққан биссектриса болады.
Яғни, үш биссектриса бір нүктеде қиылысады.
Биссектрисалардың қиылысу нүктесін І әрпімен белгілейміз
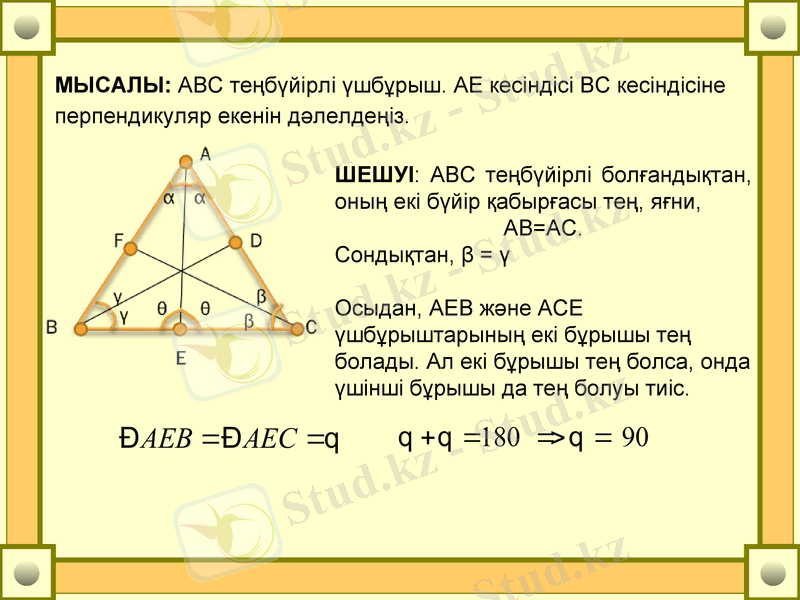
МЫСАЛЫ: АВС теңбүйірлі үшбұрыш. АЕ кесіндісі ВС кесіндісіне перпендикуляр екенін дәлелдеңіз.
ШЕШУІ: АВС теңбүйірлі болғандықтан, оның екі бүйір қабырғасы тең, яғни,
AB=AC.
Сондықтан, β = γ
Осыдан, АЕВ және АСЕ үшбұрыштарының екі бұрышы тең болады. Ал екі бұрышы тең болса, онда үшінші бұрышы да тең болуы тиіс.

Үшбұрыштың тамаша нүктелері
Үшбұрыштың тамаша нүктелері деп төрт нүктені айтамыз.
Олар: үшбұрыштың
1) биссектрисаларының қиылысу нүктесі
2) медианаларының қиылысу нүктесі
3) биіктіктерінің қиылысу нүктесі
4) қабырғаларына жүргізілген орта перпендикулярлардың қиылысу нүктесі



- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz