Тік бұрышты үшбұрыштар: қасиеттері, ұқсастық пен теңдік белгілері және Пифагор, синус пен косинус теоремалары



Тік бұрышты үшбұрыш, тік бұрышты үшбұрыштың тік бүрышынан түсірілген биссектриса, биіктік, медианасының қасиеттерін дәлелдеу және тік бұрышты үшбұрыштың ұқсастық және теңдік белгілері. Пифагор теоремасы
Тік бұрышты үшбұрыштың бұрыштары мен қабырғаларының арасындағы қатыстар. Косинустар теоремасы. Синустар теоремасы. Үшбұрыштардың периметрін және ауданын табу
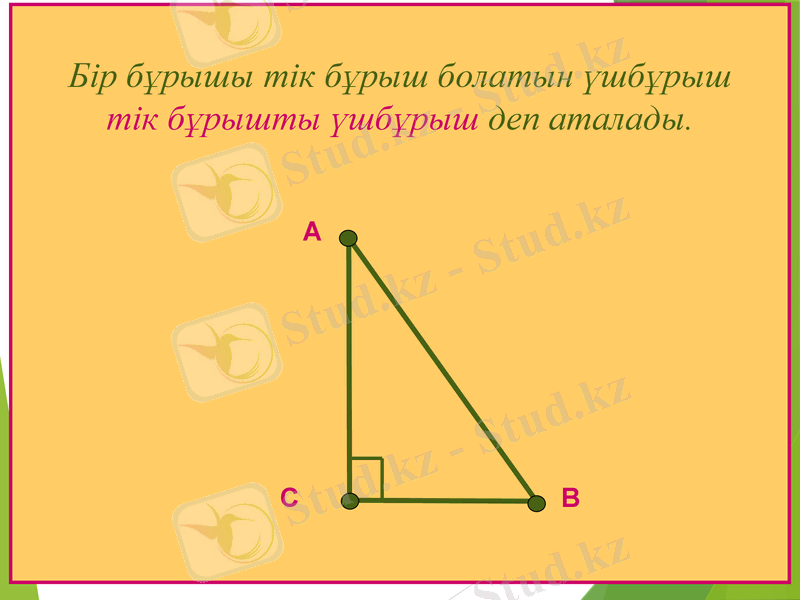
А
В
С
Бір бұрышы тік бұрыш болатын үшбұрыш тік бұрышты үшбұрыш деп аталады.
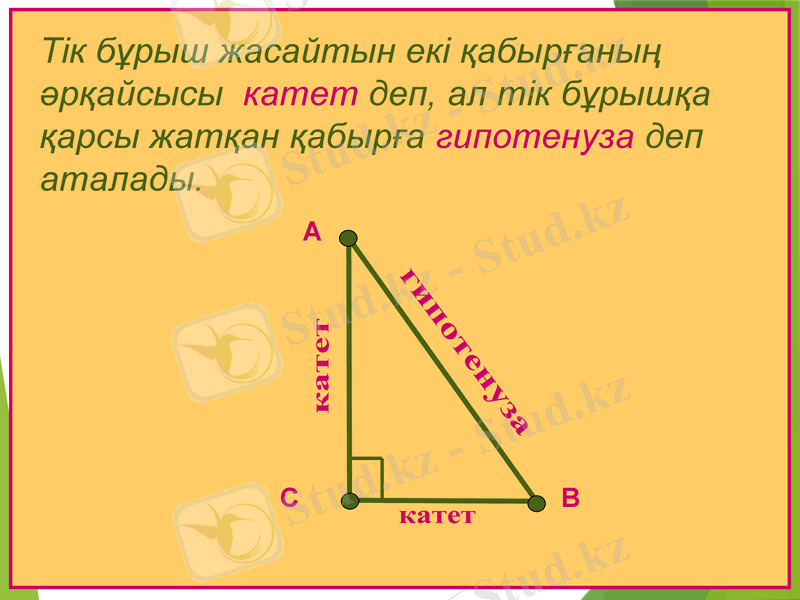
А
В
С
Тік бұрыш жасайтын екі қабырғаның әрқайсысы катет деп, ал тік бұрышқа қарсы жатқан қабырға гипотенуза деп аталады.
катет
катет
гипотенуза

Теорема
30° - қа тең бұрышқа қарсы жатқан катет
гипотенузаның жартысына тең.
Бер: ∆ АВС С = 90° B = 30°
А
B
C
30°
60°
Дәлелдеуі : ∆ ВСD тік бұрышты үшбұрышын саламыз. СВD= 30°
∆ АВD үшбұрышының барлық бұрыштары 60° -қа тең,
яғни ∆ АВD - тең қабырғалы.
АС = ½ AD, AD = AB АС = ½ AB
D
60°
30°
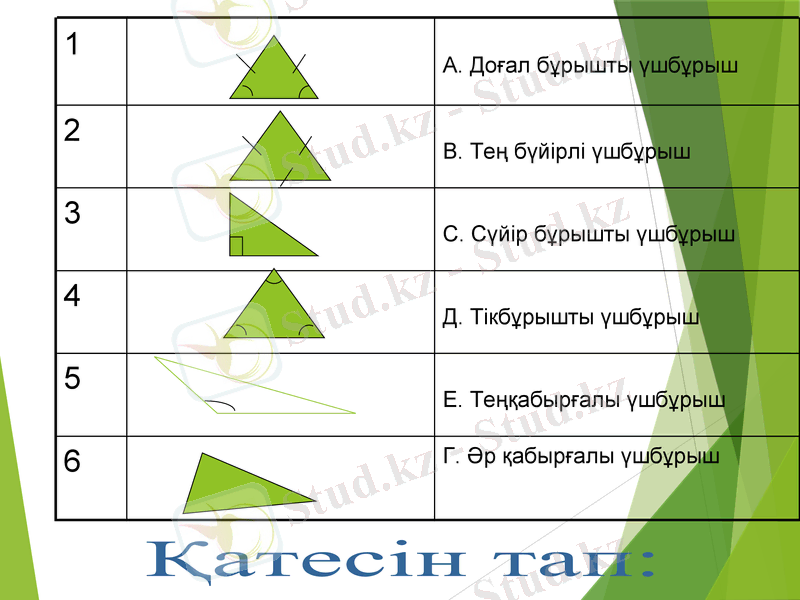
1
А. Доғал бұрышты үшбұрыш
2
В. Тең бүйірлі үшбұрыш
3
С. Сүйір бұрышты үшбұрыш
4
Д. Тікбұрышты үшбұрыш
5
Е. Теңқабырғалы үшбұрыш
6
Г. Әр қабырғалы үшбұрыш
Қатесін тап:

1
В. Тең бүйірлі үшбұрыш
2
Е. Тең қабырғалы үшбұрыш
3
Д. Тікбұрышты үшбұрыш
4
С. Сүйір бұрышты үшбұрыш
5
А. Доғал бұрышты үшбұрыш
6
Г. Әрқабырғалы үшбұрыш

Егер бір тік бұрышты үшбұрыштың катеттері екінші тік бұрышты үшбұрыштың сәйкес катеттеріне тең болса, онда мұндай тік бұрышты үшбұрыштар тең болады.
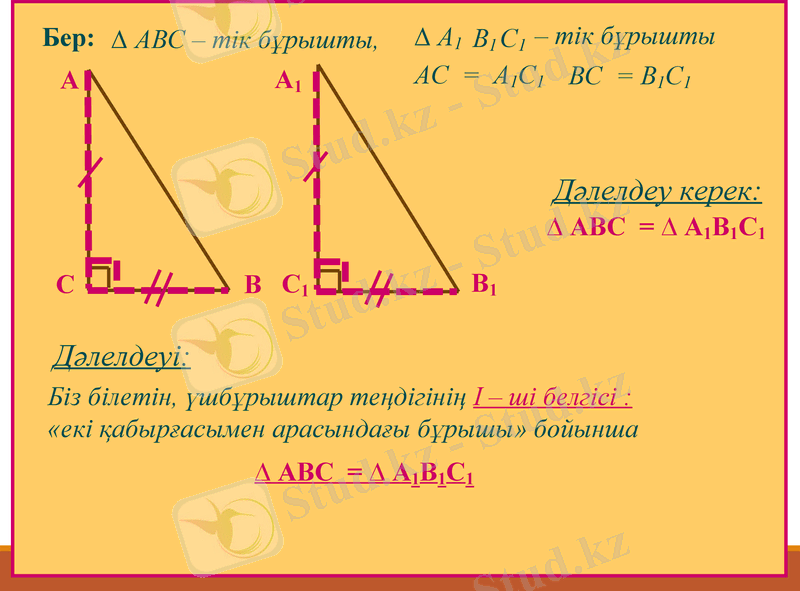
Бер:
В
А
∆ А1
С
С1
В1
АС = А1С1
Біз білетін, үшбұрыштар теңдігінің І - ші белгісі :
«екі қабырғасымен арасындағы бұрышы» бойынша
Дәлелдеуі:
∆ АВС - тік бұрышты,
- тік бұрышты
А1
В1
С1
Дәлелдеу керек:
ВС = В1С1
∆ АВС = ∆ А1В1С1
∆ АВС = ∆ А1В1С1

Егер бір тік бұрышты үшбұрыштың катеті және оған іргелес жатқан сүйір бұрышы екінші тік бұрышты үшбұрыштың сәйкес катеті мен оған іргелес жатқан сүйір бұрышына тең болса, мұндай тік бұрышты үшбұрыштар тең болады.
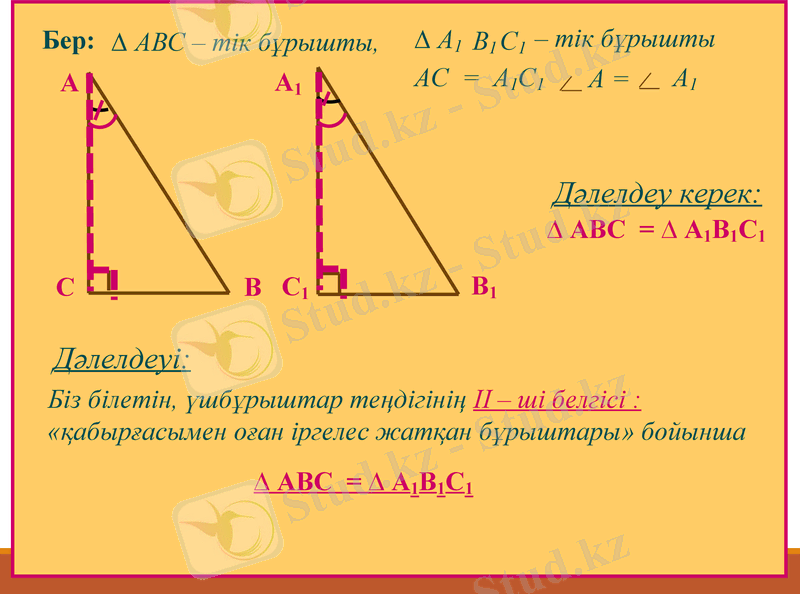
Бер:
В
А
∆ А1
С
С1
В1
АС = А1С1
Біз білетін, үшбұрыштар теңдігінің ІІ - ші белгісі :
«қабырғасымен оған іргелес жатқан бұрыштары» бойынша
Дәлелдеуі:
∆ АВС - тік бұрышты,
- тік бұрышты
А1
В1
С1
Дәлелдеу керек:
А =
∆ АВС = ∆ А1В1С1
∆ АВС = ∆ А1В1С1
А1

Егер бір тік бұрышты үшбұрыштың гипотенузасы мен сүйір бұрышы екінші тік бұрышты үшбұрыштың гипотенузасы мен сәйкес сүйір бұрышына тең болса, онда мұндай тік бұрышты үшбұрыштар тең болады.
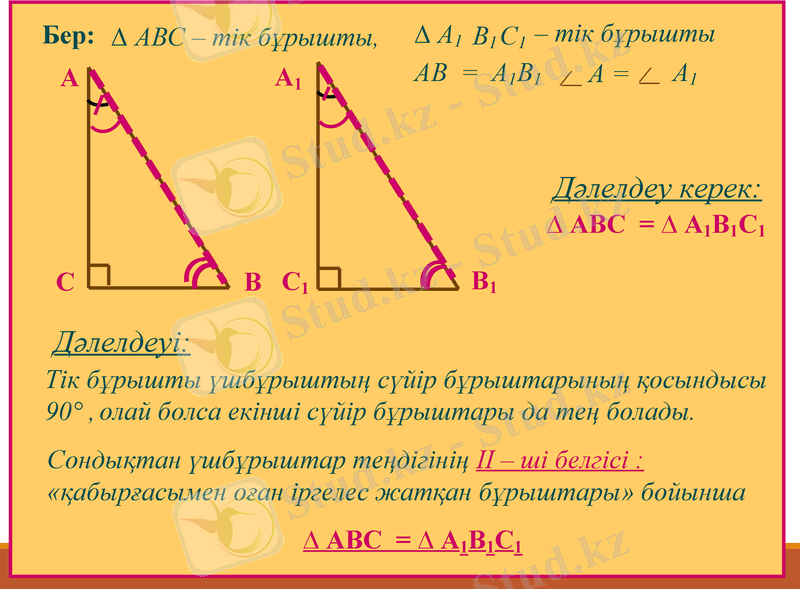
Бер:
В
А
∆ А1
С
С1
В1
АВ = А1В1
Тік бұрышты үшбұрыштың сүйір бұрыштарының қосындысы
90°,
Дәлелдеуі:
∆ АВС - тік бұрышты,
- тік бұрышты
А1
В1
С1
Дәлелдеу керек:
А =
∆ АВС = ∆ А1В1С1
∆ АВС = ∆ А1В1С1
Сондықтан үшбұрыштар теңдігінің ІІ - ші белгісі :
«қабырғасымен оған іргелес жатқан бұрыштары» бойынша
А1
олай болса екінші сүйір бұрыштары да тең болады.

Егер бір тік бұрышты үшбұрыштың гипотенузасы мен катеті екінші тік бұрышты үшбұрыштың сәйкес гипотенузасы мен катетіне тең болса, онда мұндай тік бұрышты үшбұрыштар тең болады.
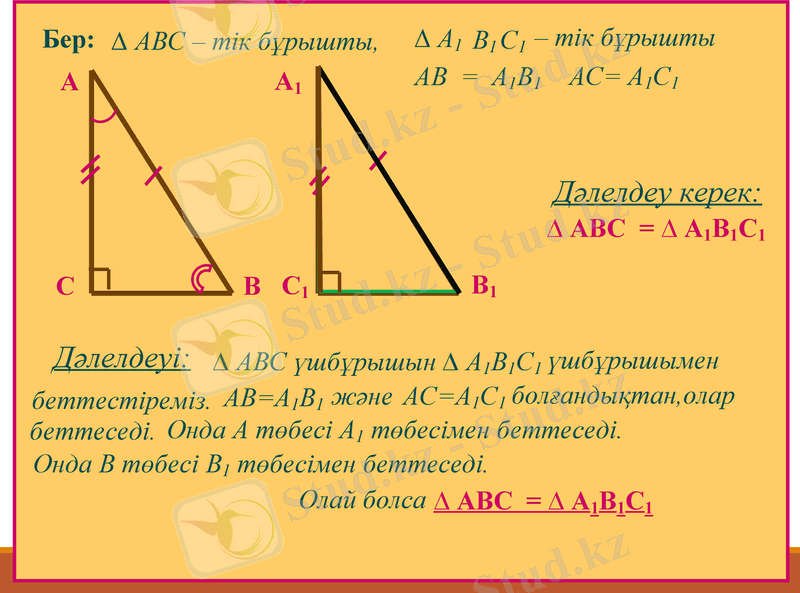
Бер:
В
А
∆ А1
С
С1
В1
АВ = А1В1
∆ АВС үшбұрышын ∆ А1В1С1
Дәлелдеуі:
∆ АВС - тік бұрышты,
- тік бұрышты
А1
В1
С1
Дәлелдеу керек:
АС= А1С1
∆ АВС = ∆ А1В1С1
үшбұрышымен
беттестіреміз.
АВ=А1В1
АС=А1С1
және
болғандықтан, олар
беттеседі.
Онда А төбесі А1 төбесімен беттеседі.
Онда В төбесі В1 төбесімен беттеседі.
Олай болса
∆ АВС = ∆ А1В1С1
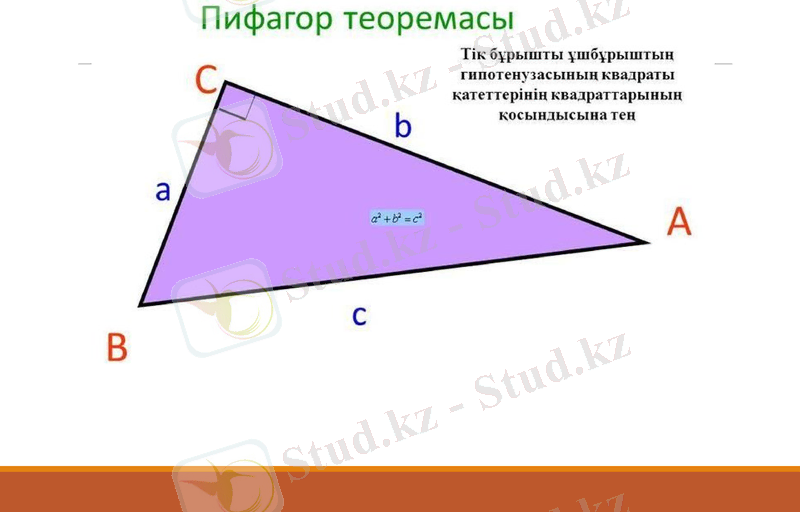
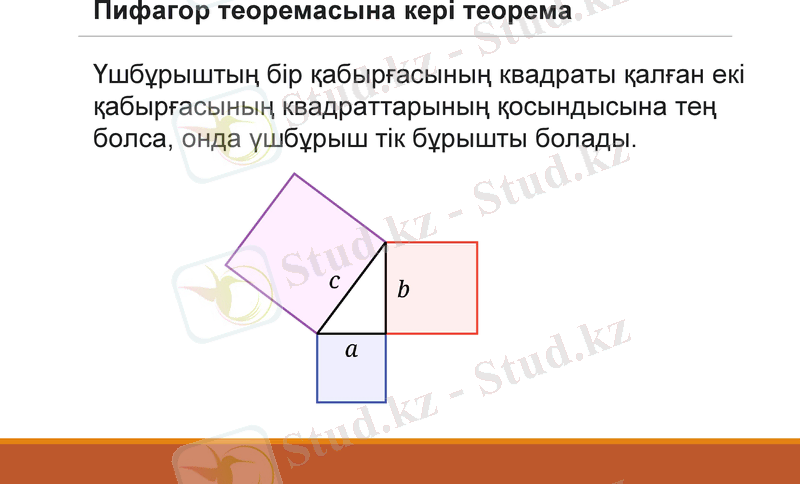
Пифагор теоремасына кері теорема
Үшбұрыштың бір қабырғасының квадраты қалған екі қабырғасының квадраттарының қосындысына тең болса, онда үшбұрыш тік бұрышты болады.

Теоременың тарихы ежелгі Қытайдан бастау алады. Ондағы негізгі назар аудартатын математикалық кітап Чу - пей. Бұл шығармада қабырғалары 3, 4, 5 - ке тең пифагор үшбұрышы туралы айтылады.
Егер тік бұрышты құрайтын 3 - ке тең қабырға мен 4 - ке тең биіктіктің ұштарын қоссақ пайда болған түзу 5 - ке тең болады.
Кантор (неміс математика тарихын зерттеуші) бұл кітапта үнді Бхаскар геометриясындағы сызбанұсқаға ұқсас сурет бар, деп есептеген.
Бұл теңдік египтіктерге б. з. д. 2300 жылы Аменемхета I патшаның кезінде белгілі болған (Берлин музейіндегі 6619 - жазбалар бойынша) .
Кантордың ойынша гарпедонаптар немесе «арқан тартушылар» тік бұрышты қабырғалары 3, 4, 5 - ке тең тікбұрышты үшбұрыштар арқылы тұрғызған. Олардың құрылу әдісін оңай көрсетуге болады. Ұзындығы 12 метрге тең арқанды алып, бір ұшынан 3 метр, екінші ұшынан 4 метр арақашықтықты өлшеп белгілейміз. Тік бұрыш 3-ке және 4-ке тең қабырғалар арасында болады. Қабырғалардың ұштарының арақашықтығы 5 - ке тең болады.

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz