Айналу беттері

Презентация қосу

Жазық қисық сызықтар
2-ші реттік қисық сызықтар
Трансценденттік қисық сызықтар
Трансценденттік қисықтар

Трансцендентные кривые: 1 — квадратриса; 2 — трактриса; 3 —
цепная линия; 4 — циклоида; 5 — архимедова спираль; 6 —
гиперболическая спираль; 7 — жезл; 8 — логарифмическая
спираль; 9 — спираль Корню; 10 — si-ci-cпираль.
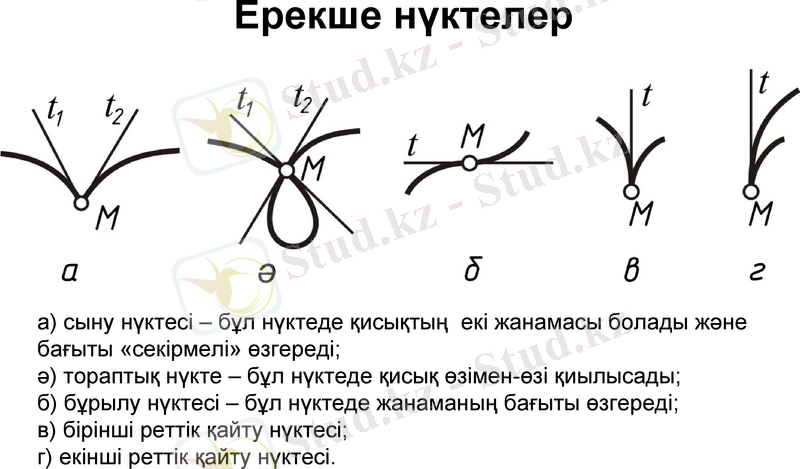
Ерекше нүктелер

а) сыну нүктесі – бұл нүктеде қисықтың екі жанамасы болады және
бағыты «секірмелі» өзгереді;
ә) тораптық нүкте – бұл нүктеде қисық өзімен-өзі қиылысады;
б) бұрылу нүктесі – бұл нүктеде жанаманың бағыты өзгереді;
в) бірінші реттік қайту нүктесі;
г) екінші реттік қайту нүктесі.
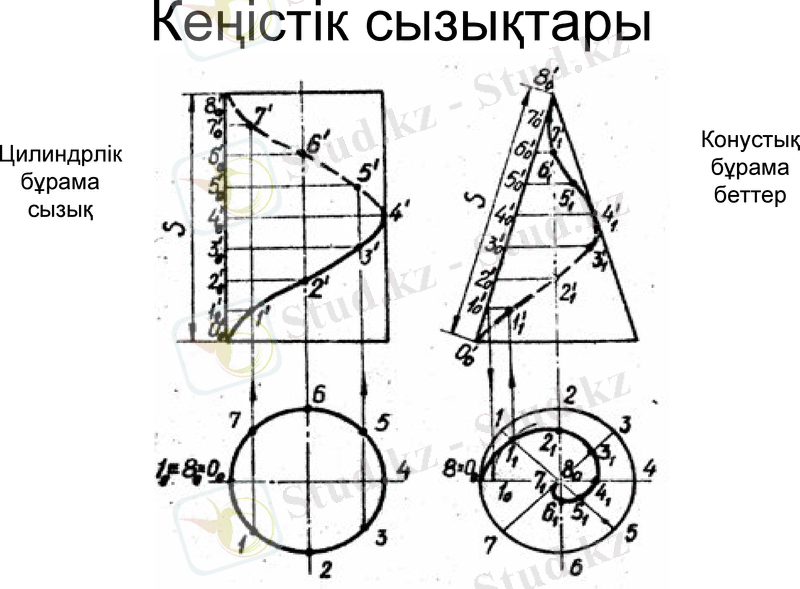
Кеңістік сызықтары
Конустық
Цилиндрлік
бұрама
бұрама
беттер
сызық
БЕТТЕРДІҢ ЖАСАЛУЫ
Сызба геометрияда
беттер кеңістікте
белгілі бір
заңдылықпен үздіксіз
қозғалатын
сызықтың
орындарының
жиыны ретінде
қарастырады. Беттің
жасалуының бұл
тәсілін
кинематикалық деп
атайды.
Беттi анықтайтын шарттарды беттiң анықтауышы деп атауға
келiсiлген. Анықтауыш – геометриялық және алгоритмдiк деп
аталатын екi бөлiктен тұрады.
Беттердің түрлері
• Айналу беттері
• Сызықтық беттер
• Бұрама беттер
• Цикликалық және топографиялық
беттер
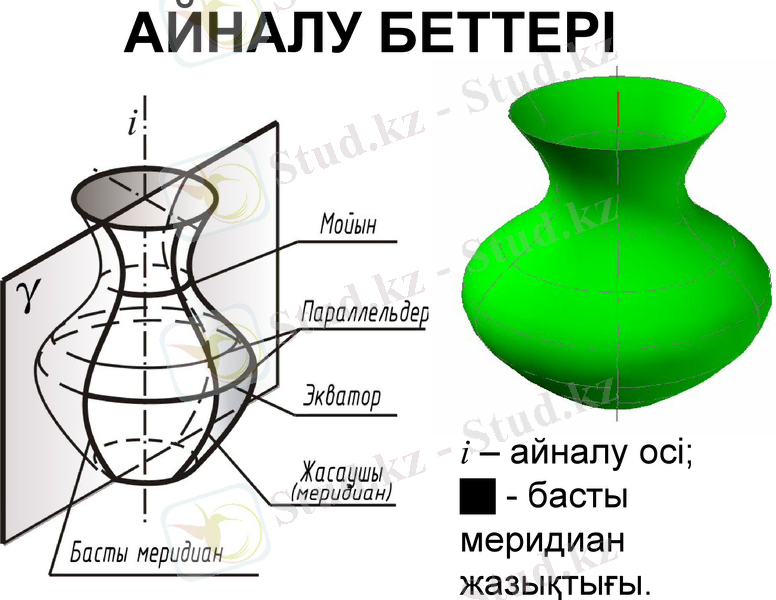
АЙНАЛУ БЕТТЕРІ

i – айналу осі;
- басты
меридиан
жазықтығы.
Конустық айналу беті

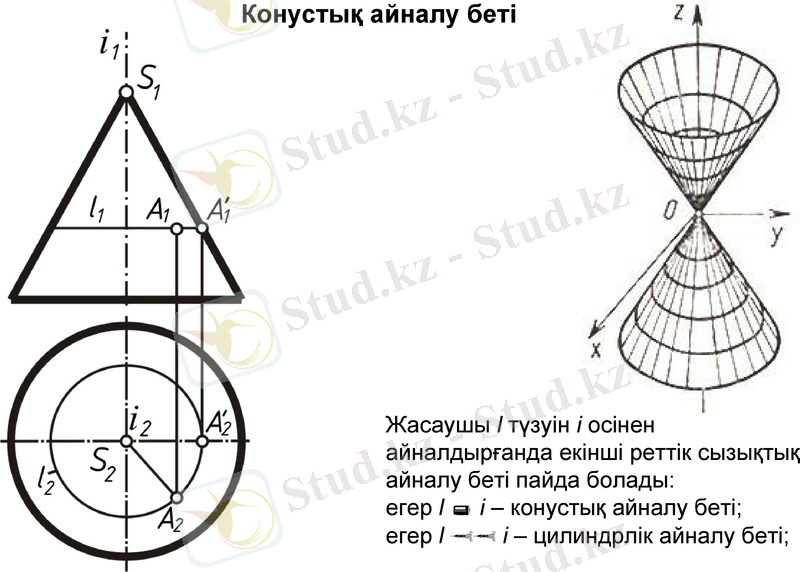
Жасаушы l түзуін i осінен
айналдырғанда екінші реттік сызықтық
айналу беті пайда болады:
егер l i – конустық айналу беті;
егер l i – цилиндрлік айналу беті;
Бір қуысты гиперболоид

егер l i – бірқуысты айналу
гиперболоиды.
• Айналу бетінің түрі жасаушының
пішіміне және оның айналу осіне
қатысты орналасуына байланысты.
Симметрия жазықтығы бар n – реттік
қисық сызығын осы симметрия
жазықтығында орналасқан айналу
осінен айналдырғанда n – реттік айналу
беті пайда болады.
2-ші реттік беттер
• 1. Сфера. Шеңберді диаметрінен айналдыру арқылы
жасалады.
• 2. Айналу эллипсоиды. Бұның меридианы эллипс
болып табылады. Егер Если эллипс өзінің үлкен осінен
айналса эллипсоид созылған деп, ал кіші осінен айналса
қысылған деп аталады.
• 3. Айналу параболоиды. Меридианы парабола болып
табылады.
• 4. Айналу гиперболоиды. Беттің меридианы –
гипербола. Егер айналу осі гиперболаның нақты осімен
сәйкес болса, екі қуысты гиперболоид, ал егер айналу осі
гиперболаның жорамал осімен сәйкес болса, бір қуысты
гиперболоид жасалады.
Сфера. Шеңберді диаметрінен
айналдыру арқылы жасалады.
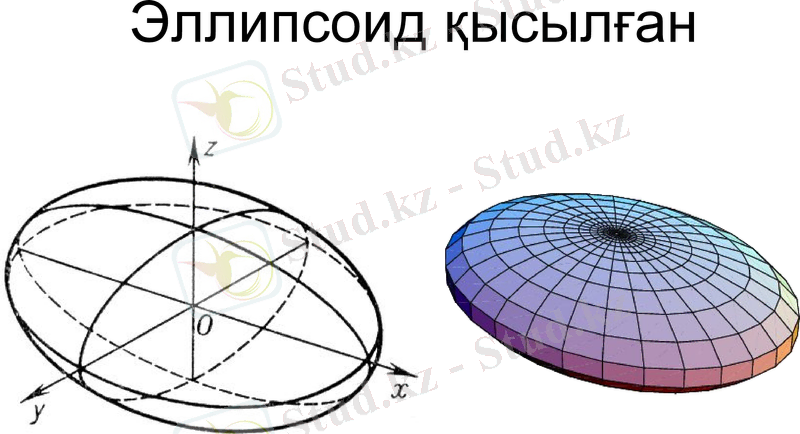
Эллипсоид қысылған
Эллипсоид созылған
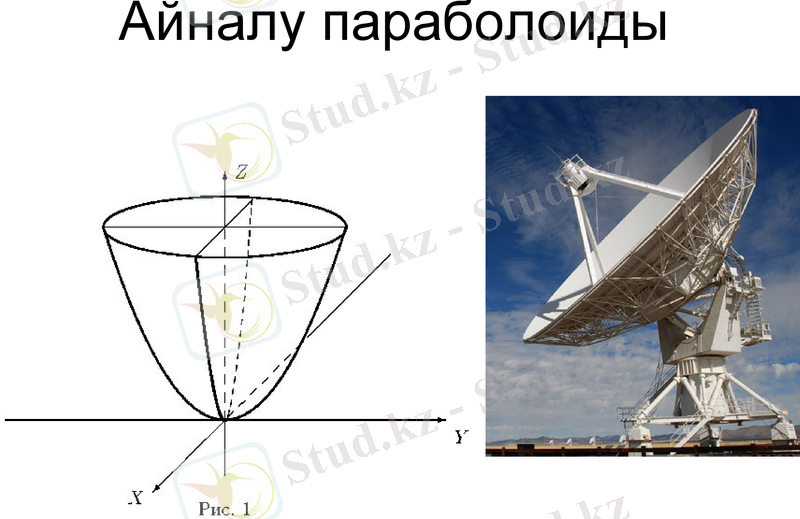
Айналу параболоиды
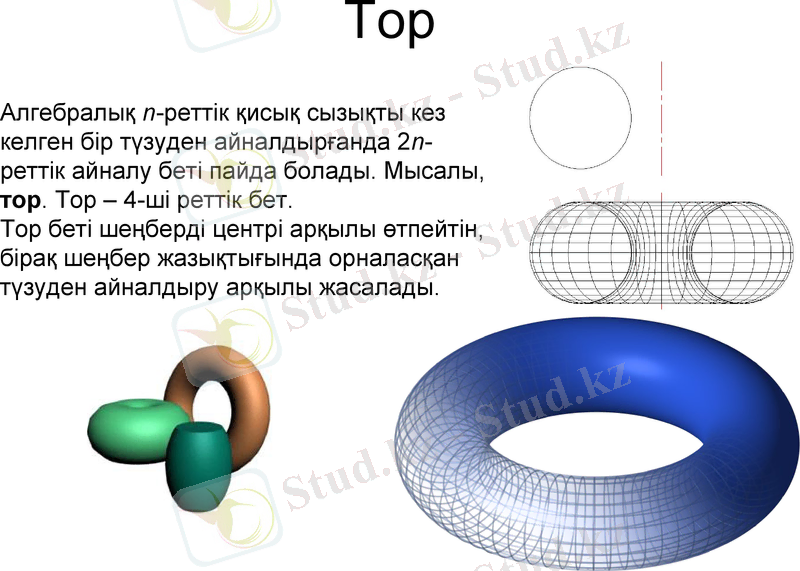
Тор
Алгебралық n-реттік қисық сызықты кез
келген бір түзуден айналдырғанда 2n-
реттік айналу беті пайда болады. Мысалы,
тор. Тор – 4-ші реттік бет.
Тор беті шеңберді центрі арқылы өтпейтін,
бірақ шеңбер жазықтығында орналасқан
түзуден айналдыру арқылы жасалады.
Сызықтық беттер
Түзудің белгілі бір заңды қозғалысынан пайда болған
бетті сызықтық деп атайды. Олар жайылатын және
жайылмайтын болып екіге бөлінеді. Жайылатын
беттер – конустық, цилиндрлік және торстық беттер.
Кеңістік сызығына жанамалар жиынынан жасалған
бетті торстық немес кері қайту қыры бар бет деп
атайды.
Жайылмайтын беттер – параллелизм жазықтығы бар
беттер (Каталан беттері): цилиндроид, коноид, қиғаш
жазықтық (гиперболалық параболоид)
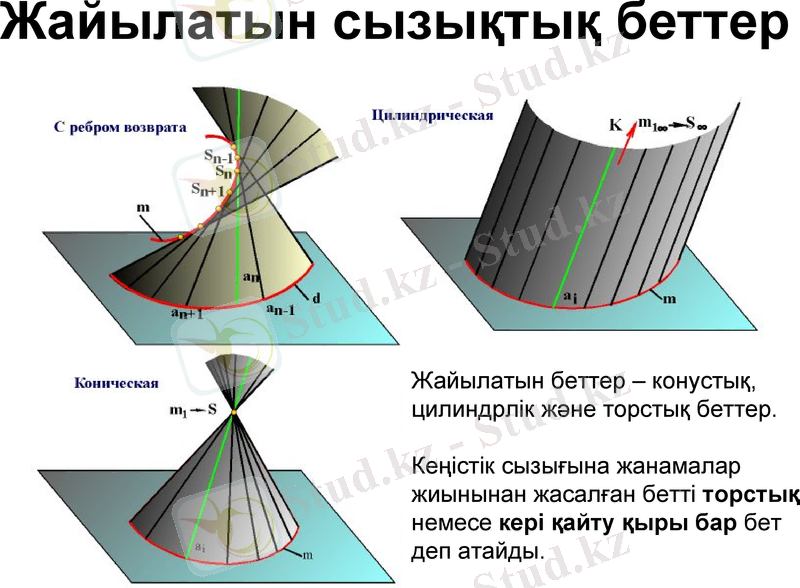
Жайылатын сызықтық беттер

Жайылатын беттер – конустық,
цилиндрлік және торстық беттер.

Кеңістік сызығына жанамалар
жиынынан жасалған бетті торстық
немесе кері қайту қыры бар бет
деп атайды.
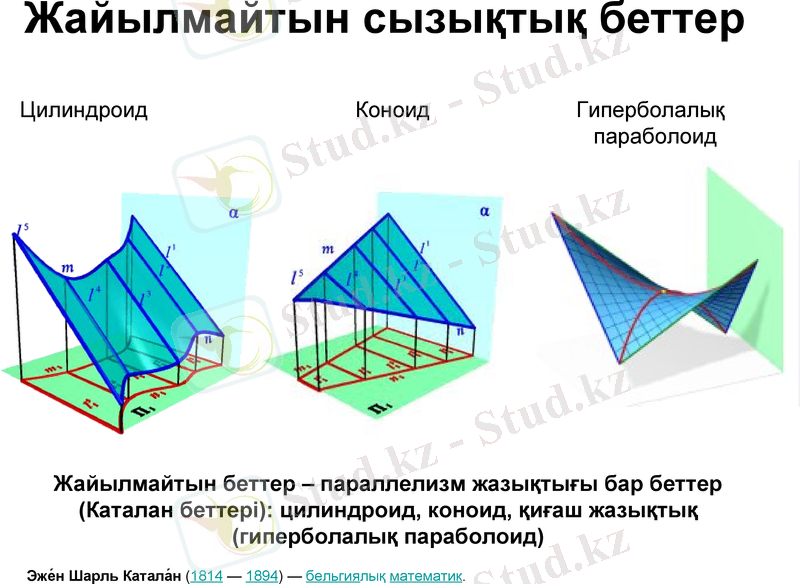
Жайылмайтын сызықтық беттер
Цилиндроид Коноид Гиперболалық

параболоид

Жайылмайтын беттер – параллелизм жазықтығы бар беттер
(Каталан беттері): цилиндроид, коноид, қиғаш жазықтық
(гиперболалық параболоид)
Эже́н Шарль Катала́н (1814 — 1894) — бельгиялық математик.
Бұрама беттер
Сызықтың бұрама қозғалысынан жасалатын
бетті бұрама бет деп атайды. Егер
жасаушы бұрама қозғалыстың осімен
қиылысатын болса, бұрама бет жабық деп
аталады, ал егер қиылыспайтын болса –
ашық деп аталады. Егер жасаушы түзу
болса бет геликоид деп аталады. Егер
жасаушы бұрама қозғалыстың осіне
перпендикуляр болса - тік, ал қиғаш
орналасса – қиғаш деп аталады. Суретте
жабық тік геликоид көрсетілген. Егер ашық
геликоидтың жасаушысы белгілі бір
цилиндрлік бұрама сызыққа жанама
қозғалса, геликоид бұрама торс деп немесе
эвольвенттік деп аталады, өйткені оның
нормаль қимасы (оське перпендикуляр)
шеңбердің эвольвентасы болып табылады.
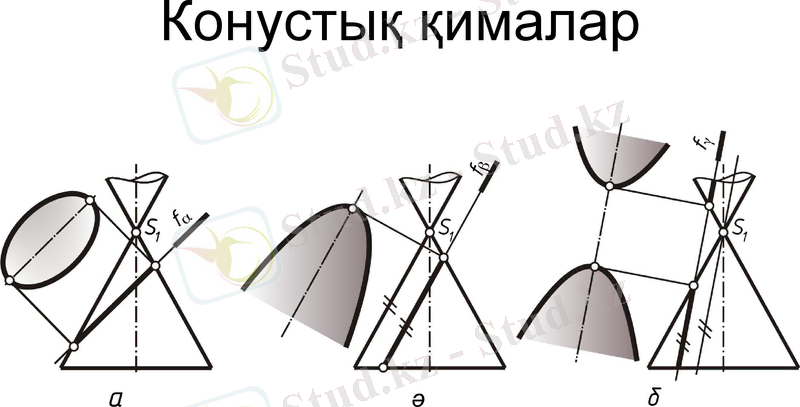
Конустық қималар

Ұқсас жұмыстар

Цилиндрлік тісті доңғалақ жасау

Қөпжақтар Айналу денелері

Буын - бір сүйекпен екінші сүйекті жалғастыратын аралық

Осьтік сорап

Карбюраторлы қозғалтқыштың қоректендіру жүйесінің құрылымы және бөлшектерінің конструкциясын жобалау

Жұмыс дөңгелегі шарикподшипниктері түріндегі екі тірекке, болат білік

Фрикциялық берілістердің артықшылықтары

Қаңқа сүйектерінің буынды байланысы, бассүйектегі буынды омыртқалар байланысы

Іштен жанатын қозғалтқыштары

Бұрғылау шығырларының тежегіштері

Пәндер