Жиын және оларға қолданылатын амалдар

Презентация қосу

Е.А. Бөкетов атындағы Қарағанды мемлекеттік университеті
«Математика және Ақпараттық технологиялар» факультеті
«Математикалық анализ және дифференциалдық теңдеулер» кафедрасы

«Жиын және оларға қолданылатын амалдар»

Орындаған: М-19-3 тобының студенті
Калинбетов Н.О.
Тексерген: Оразбекова Рауана Толеукутовна
Жиын және оларға
қолданылатын амалдар
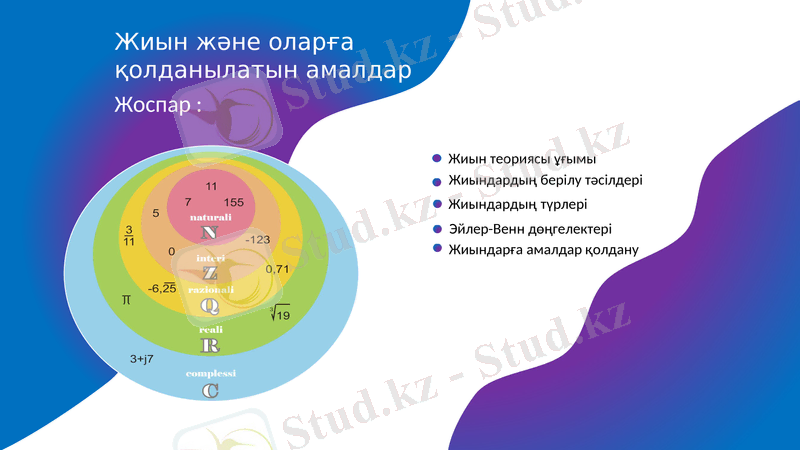
Жоспар :

Жиын теориясы ұғымы
Жиындардың берілу тәсілдері
Жиындардың түрлері
Эйлер-Венн дөңгелектері
Жиындарға амалдар қолдану
Жиын ұғымы анықтауға болмайтын
алғашқы ұғымдардың бірі. Жиынды
құрайтын объектілерді жиынның
элементтері дейді.

1- ден 10-ға дейінгі сандар, натурал
сандар, бір таңбалы сандар, үшбұрыш
шаршылар т.с.с.

Осы әр түрлі жиынтықтарды
жиындар деп атайды.
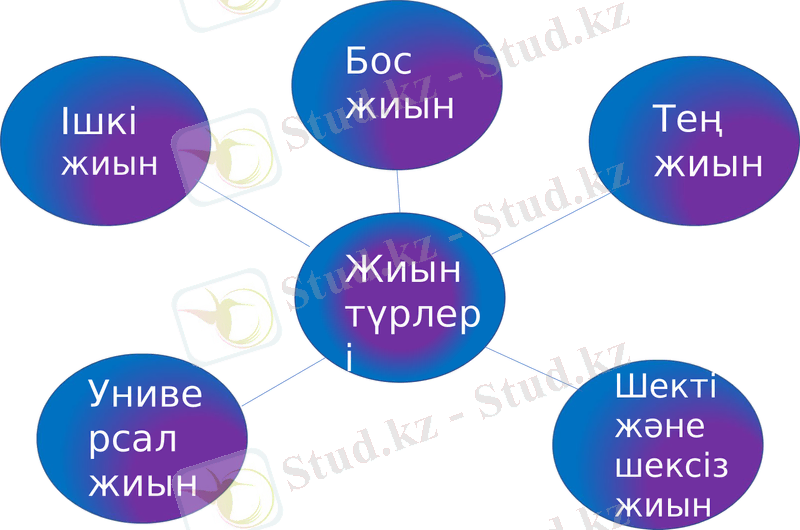
Жиындардың берілу
тәсілдері

Жиынды оның А- жиыны 3,4,5 және 6
элементтерін атау сандарынан тұрады
десек, онда біз жиын
арқылы аныктап беруге
берілген дейміз. А
болады, егер кез келген (3,4,5,6).
обьектіні жиынға тиісті
немесе тиісті емес
екенін, айта алсак, онда
жиын берілген деп
есептейміз.
Бос
Ішкі жиын Тең
жиын жиын

Жиын
түрлер
і
Униве Шекті
рсал және
шексіз
жиын
жиын
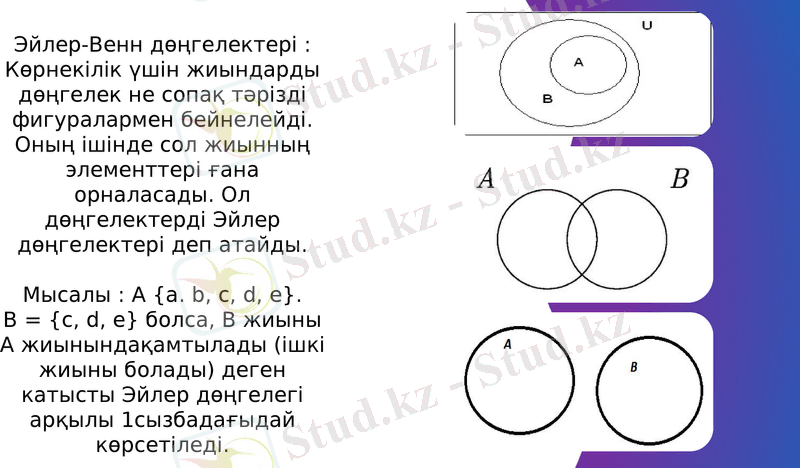
Эйлер-Венн дөңгелектері :
Көрнекілік үшін жиындарды
дөңгелек не сопақ тәрізді
фигуралармен бейнелейді.
Оның ішінде сол жиынның
элементтері ғана
орналасады. Ол
дөңгелектерді Эйлер
дөңгелектері деп атайды.

Мысалы : А {а. b, c, d, e}.
В = {c, d, e} болса, В
жиыны А
жиынындақамтылады (ішкі
жиыны болады) деген
катысты Эйлер дөңгелегі
арқылы 1сызбадағыдай
Жиындардың қиылысуы :
Анықтама: А жиынына да В
жиынынада тиісті элементтерден
тұратын C жиынын A және В
жиындарының қиылысуы деп
атайды.
А және В жиындарының
қиылысуы былай белгіленеді: ˄ ;
Мысалы: А = {2, 4, 6, 8} және В =
{5, 6, 7, 8, 9} жиындары берілсін.
А және В жиындарының ортақ
элементтерінен тұратын С
жиынын кұрайық, С={6, 8}.
Сонымен алынған C жиыны А
және В жиындарының қиылысуы
деп аталады.
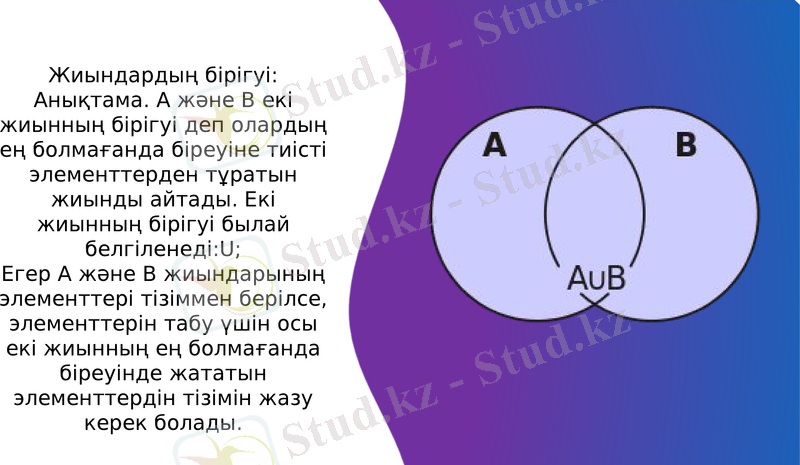
Жиындардың бірігуі:
Анықтама. А және В екі
жиынның бірігуі деп олардың
ең болмағанда біреуіне тиісті
элементтерден тұратын
жиынды айтады. Екі
жиынның бірігуі былай
белгіленеді:U;
Егер А және В жиындарының
элементтері тізіммен берілсе,
элементтерін табу үшін осы
екі жиынның ең болмағанда
біреуінде жататын
элементтердін тізімін жазу
керек болады.
Жиындардың айырымы:
А жиыны мен В жиынының айырмасы
деп А жиынының В жиынында
жатпайтын элементтерінен тұратын
жиынды айтады. Айырманың
анықтамасын былай жазып
көрсетуге болады:B∉А және х ∈A\B
= {x | x}
Мысалы.
1) Егер А = {1, 3, 5, 6}, B = {5, 6,
7, 8, 9} болса, онда В \ А = {7, 8,
9}.
2) Егер А = (-2; 3], B = [1; 4]
болса, онда B\ А = (3; 4]
Жиынның толықтауышы:
A⊂B жиыны А жиынының
ішкіжиыны болсын, яғни В.
В жиынында жатпайтын A
жиынының барлық
элементтерінің жиынын В-
нің толықтауыш жиыны
деп атайды.
B жиынынатолықтауыш
жиынды таңбасымен
белгілейді.
Жиындарға қолданылатын амалдардың заңдары:
Жиындардың қиылысуы және бірігуі коммутативті
болады
A⋂B = B⋂A
A∪B = B∪A
Жиындардың қиылысуы және бірігуі ассоциативті
болады
(A⋂B)⋂C= A⋂(B C)
C∪ (B∪C) = (A∪B)∪A
Жиындардың қиылысу және бірігу амалдарын
байланыстыратындистрибутивтік заңы орынды болады
A⋂(B∪C) = (A⋂B)∪(A⋂C)
A∪(B⋂C) = (A∪B)⋂(A∪C)
Назарларыныз
ға Рахмет !!!

Ұқсас жұмыстар

Жиындардың бірігуі

МАТЕМАТИКАЛЫҚ ТАЛДАУҒА КІРІСПЕ

Иррационал сандар

Арифметикалық есептер

Мектептегі дискретті математика элементтерін оқыту әдістемесі

Жалпы білім беретін мектепте нақты сандарды оқытып - үйрету

Алгоритмдік тілдің алфавиті, синтаксисі және семантикасы

Геометрия бөлімінің бөлімшелері

Матрицаларды көбейту

Комплекс сандардың геометрияда қолдануы

Пәндер