Регрессиялық талдау

Тақырыбы:

Регрессиялық талдау

Дәріс жоспары:

Регрессиялық талдау: негізгі түсініктер.

Регрессия түрлері.

Сызықты регрессия параметрлерін ең кіші квадраттар әдісі бойынша бағалау.

Регрессия коэффициентінің маңыздылығы туралы болжамды тексеру.

Регрессия теңдеуінің маңыздылығы туралы болжамды тексеру.

Детерминация коэффициенті.

Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы.

Регрессиялық талдау

«Регрессия» терминін алғаш рет биометрияның негізін салушы Ф. Гальтон енгізген, оның ойын ізбасары К. Пирсон дамытқан.

Ф. Гальтон (1822-1911)

К. Пирсон

(1857-1936)

Регрессиялық талдау - бір немесе бірнеше белгілердің (факторлық белгілердің) және салдардың (нәтижелі белгілердің) арасындағы байланысты өлшеуге мүмкіндік беретін статистикалық өңдеу әдісі.

Регрессиялық талдау: негізгі түсініктер

Белгі - бұл зерттелетін құбылыстың немесе үдерістің негізгі ерекшелігі.

Нәтижелік белгі - зерттелелетін көрсеткіш.

Факторлық белгі - нәтижелік белгінің мәніне әсер ететін көрсеткіш.

Регрессиялық талдаудың мақсаты регрессия теңдеуі түрінде берілген орташа мәннің (у) нәтижелік белгісінің, (х1, х2, …, хn), факторлық белгіге функционалдық байланысын бағалау болып табылады:

Регрессиялық талдау: негізгі түсініктер

РЕГРЕССИЯ

ЖҰПТАСҚАН

у = f (x)

КӨПШЕ

Регрессиялық талдау келесі кезеңдерден тұрады:

функция түрін анықтаудан;

регрессия коэффициенттерін анықтаудан;

нәтижелі белгінің теориялық мәндерін есептеуден;

регрессия коэффициентінің статистикалық маңыздылығын тексеруден;

регрессия теңдеуінің статистикалық маңыздылығын тексеруден.

Дәріс жоспары:

Регрессиялық талдау: негізгі түсініктер.

Регрессия түрлері.

Сызықты регрессия параметрлерін ең кіші квадраттар әдісі бойынша бағалау.

Регрессия коэффициентінің маңыздылығы туралы болжамды тексеру.

Регрессия теңдеуінің маңыздылығы туралы болжамды тексеру.

Детерминация коэффициенті.

Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы.

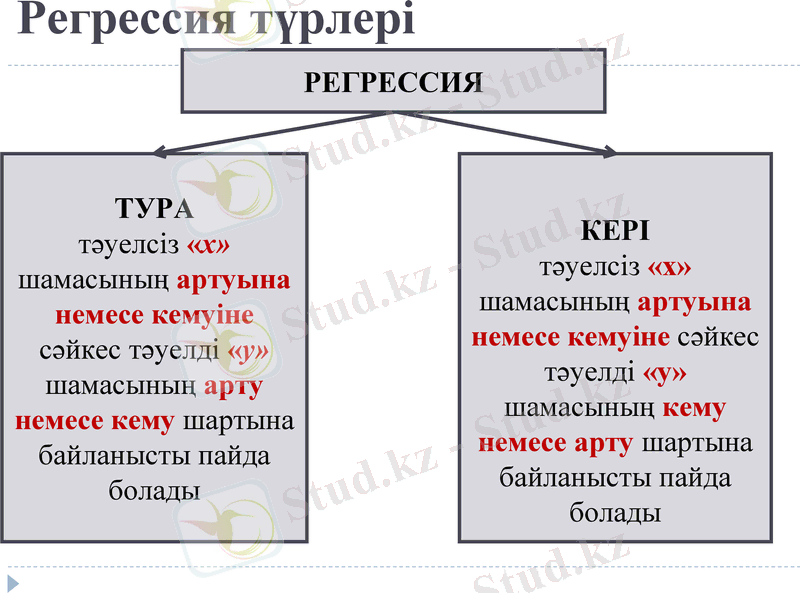
Регрессия түрлері

РЕГРЕССИЯ

ТУРА

тәуелсіз «х» шамасының артуына немесе кемуіне сәйкес тәуелді «у» шамасының арту немесе кему шартына байланысты пайда болады

КЕРІ

тәуелсіз «х» шамасының артуына немесе кемуіне сәйкес тәуелді «у» шамасының кему немесе арту шартына байланысты пайда болады

Жұптасқан регрессия теңдеуілер

Байланысты сипаттау үшін келесі жұптасқан регрессия теңдеулерінің түрлерін қолданады:

у=a+bx - сызықтық;

y=eax+b - экспоненциалды;

y=a+b/x - гиперболалық;

y=a+b1x+b2x2 - параболалық;

y=abx - көрсеткіштік және т. б.

мұндағы a, b1, b2 - теңдеудің коэффициенттері (параметрлері) ; у - нәтижелі белгі; х - факторлық белгі.

Дәріс жоспары:

Регрессиялық талдау: негізгі түсініктер.

Регрессия түрлері.

Сызықты регрессия параметрлерін ең кіші квадраттар әдісі бойынша бағалау.

Регрессия коэффициентінің маңыздылығы туралы болжамды тексеру.

Регрессия теңдеуінің маңыздылығы туралы болжамды тексеру.

Детерминация коэффициенті.

Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы.

Сызықты регрессия параметрлерін ең кіші квадраттар әдісі бойынша бағалау

Регрессия теңдеуін құру, оның коэффициенттерін (параметрлерін) бағалауға алып келеді, ол үшін ең кіші квадраттар әдісі қолданылады.

Ең кіші квадраттар әдісі: болғанда параметрлерді бағалауға мүмкіндік береді.

Ең кіші квадраттар әдісі бойынша сызықты регрессия у=a+bх теңдеуінің параметрлерін анықтау формуласы:

Дәріс жоспары:

Регрессиялық талдау: негізгі түсініктер.

Регрессия түрлері.

Сызықты регрессия параметрлерін ең кіші квадраттар әдісі бойынша бағалау.

Регрессия коэффициентінің маңыздылығы туралы болжамды тексеру.

Регрессия теңдеуінің маңыздылығы туралы болжамды тексеру.

Детерминация коэффициенті.

Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы.

Регрессия коэффициентінің маңыздылығын тексерудің сызбасы

1) Н0: a=0, b=0.

Н1: a≠0, b≠0.

2) р=0, 05 - маңыздылық деңгейі.

3) мұндағы mb, ma - кездейсоқ қателіктер:

4) tкесте(р; f), мұндағы f=n-k-1, n - бақылау саны, k - айнымалылары «х» теңдеудегі параметрлер саны.

5) Егер болса, онда Н0 қабылданбайды, яғни коэффи-циент маңызды.

Егер болса, онда Н0 қабылданады, яғни коэффициент маңызды емес.

Дәріс жоспары:

Регрессиялық талдау: негізгі түсініктер.

Регрессия түрлері.

Сызықты регрессия параметрлерін ең кіші квадраттар әдісі бойынша бағалау.

Регрессия коэффициентінің маңыздылығы туралы болжамды тексеру.

Регрессия теңдеуінің маңыздылығы туралы болжамды тексеру.

Детерминация коэффициенті.

Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы.

Регрессия теңдеуінің маңыздылығын тексерудің сызбасы

1) Н0: регрессия теңдеуі маңызды емес.

Н1: регрессия теңдеуі маңызды.

2) р=0, 05 - маңыздылық деңгейі.

мұндағы n - бақылау саны; k - айнымалылары «х» теңдеудегі параметрлер саны; у - нәтижелі белгінің нақты мәні; yx - нәтижелі белгінің теориялық мәні; - жұпталған корреляция коэффициенті.

4) Fкесте(р; f1; f2),

мұндағы f1=k, f2=n-k-1- еркіндік дәрежелерінің саны

5) Егер Fесеп>Fкесте, онда регрессия теңдеуі дұрыс таңдалған.

Ұқсас жұмыстар

КӨПТІК СЫЗЫҚТЫҚ РЕГРЕССИЯ МОДЕЛЬ

ЭКОНОМИКАЛЫҚ ТАЛДАУДЫҢ ӘДІСТЕРІ

Статистиканың басқа қоғамдық ғылымдардан айырмашылығы

Қаржылық болжау

Урбандалу процестерін моделдеудің ақпараттық жүйесін құру

Тәуелді және тәуелсіз үлгілер

Кездейсоқ. жасаушылардың автокорреляциясы

Көпфакторлы дисперсиялық талдау