Өрістің математикалық сипаттамасы және негізгі түрлері: гравитациялық, электрлік, магниттік және электромагниттік



ОҢТҮСТІК ҚАЗАҚСТАН МЕМЛЕКЕТТІК ПЕДАГОГИКАЛЫҚ УНИВЕРСИТЕТІ
ПРЕЗЕНТАЦИЯ
Тобы: 1510-19а
Орындағандар:Абдыр Индира, Зейлан Назкен, Рысалы Құндыз, Спатаева Жансая
Өрістің математикалық сипаттамасы

Өріс- еркіндік дәрежесі шексіз көп физикалық жүйе, материяның негізгі түрі. Электрлік, гравитациялық, ядролық және әлсіз әсерлесуге қатысатын нысандардың өз өрістерітері болады. Өріс - осы нысандардың әсерлесуін тасымалдайтын орта. Бір бөлшектің күш әсері екінші бөлшекке өріс арқылы біртіндеп шекті уақытта беріледі. Әсерлесу кезінде өріс бірінші бөлшектің энергиясы мен импульсының бір бөлігін екінші бөлшекке қарай тасымалдайды. Сондықтан өріс материяның негізгі түрі болып табылады. Өріс ұғымын тұтас ортаның қасиеттерін зерттеуге де қолданады. Бұл жерде ортаның әр нүктесінің күйін анықтайтын физикалық шамалар жиынтығы (қысым, температура, тартылыс күші, т. б. ) өріс болып табылады.
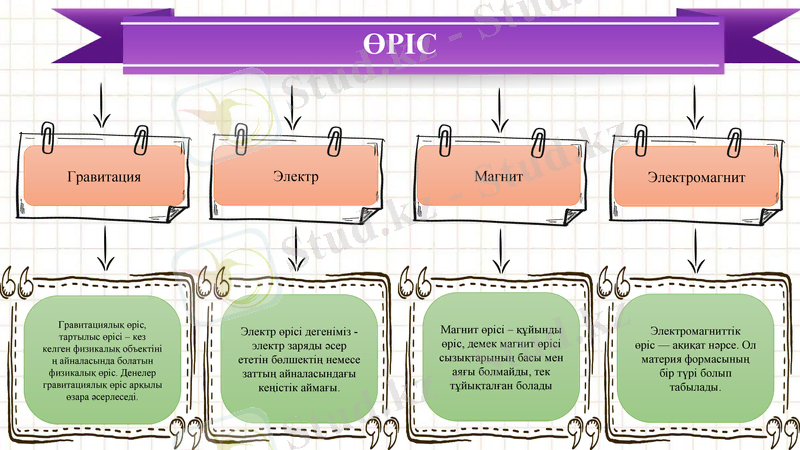
Өріс
Гравитация
Электр
Магнит
Электромагнит
Гравитациялық өріс, тартылыс өрісі - кез келген физикалық объектінің айналасында болатын физикалық өріс. Денелер гравитациялық өріс арқылы өзара әсерлеседі.
Электр өрісі дегеніміз - электр заряды әсер ететін бөлшектің немесе заттың айналасындағы кеңістік аймағы.
Магнит өрісі - құйынды өріс, демек магнит өрісі сызықтарының басы мен аяғы болмайды, тек тұйықталған болады
Электромагниттік өріс - ақиқат нәрсе. Ол материя формасының бір түрі болып табылады.
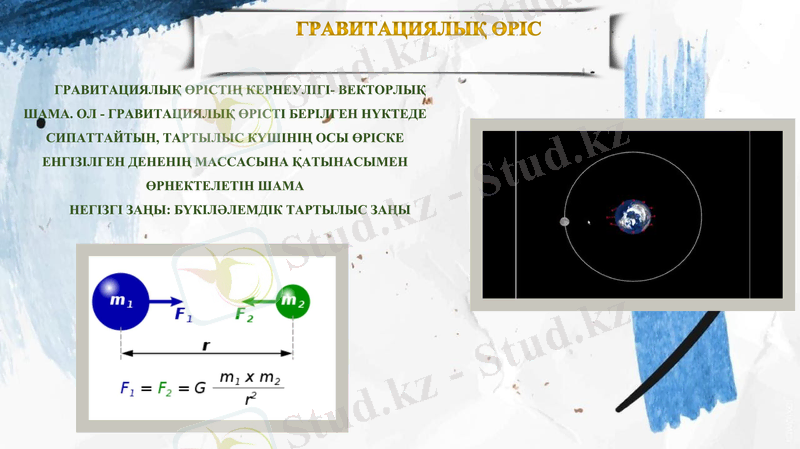
Гравитациялық өріс
Гравитациялық өрістің кернеулігі- векторлық шама. Ол - Гравитациялық өрісті берілген нүктеде сипаттайтын, тартылыс күшінің осы өріске енгізілген дененің массасына қатынасымен өрнектелетін шама
Негізгі заңы: Бүкіләлемдік тартылыс заңы
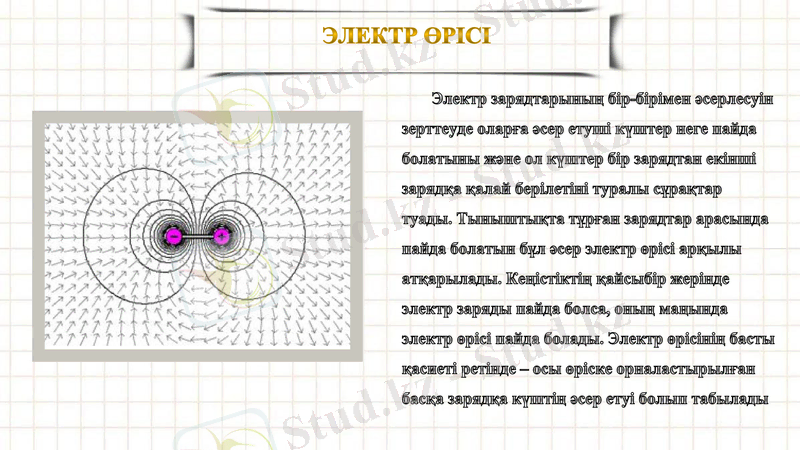
Электр өрісі
Электр зарядтарының бір-бірімен әсерлесуін зерттеуде оларға әсер етуші күштер неге пайда болатыны және ол күштер бір зарядтан екінші зарядқа қалай берілетіні туралы сұрақтар туады. Тыныштықта тұрған зарядтар арасында пайда болатын бұл әсер электр өрісі арқылы атқарылады. Кеңістіктің қайсыбір жерінде электр заряды пайда болса, оның маңында электр өрісі пайда болады. Электр өрісінің басты қасиеті ретінде - осы өріске орналастырылған басқа зарядқа күштің әсер етуі болып табылады

Магнит өрісі
Магнит өрісін магнит индукциясының сызықтары арқылы бейнелейді. Магнит индукциясының сызығы дегеніміз - жанамасы әрбір нүктеде магнит индукциясы векторының В бағытымен сәйкес келетін қисық.
Қорытынды магнит өрісін (В) сипаттайды, ол барлық макро және микротоқтармен түзіле отырып, әртүрлі ортада әртүрлі шамаға ие болады. Макротоктың тұрақты мәнінде бірақ, әртүрлі ортада әртүрлі болуы мүмкін. Кернеулік векторы (H) - Макротоқтағы магнит өрісін сипаттайды.

Электромагниттік өріс
Электромагниттік өріс - ақиқат нәрсе. Ол материя формасының бір түрі болып табылады. Материя формасының екінші түрі зат.
Электр зарядтары айнымалы қозғалыс (мысалы, тербеліс) жасағанда, олардың туғызатын айнымалы электромагнитгік өрісі кеңістіктің бір нүктесінен екінші нүктесіне тарайды.
Электр зарядтары айнымалы қозғалғанда, яғни кез келген айнымалы тоқта электр өрісі де, магнит өрісі де уақыт өтуіне қарай өзгеріп отырады.
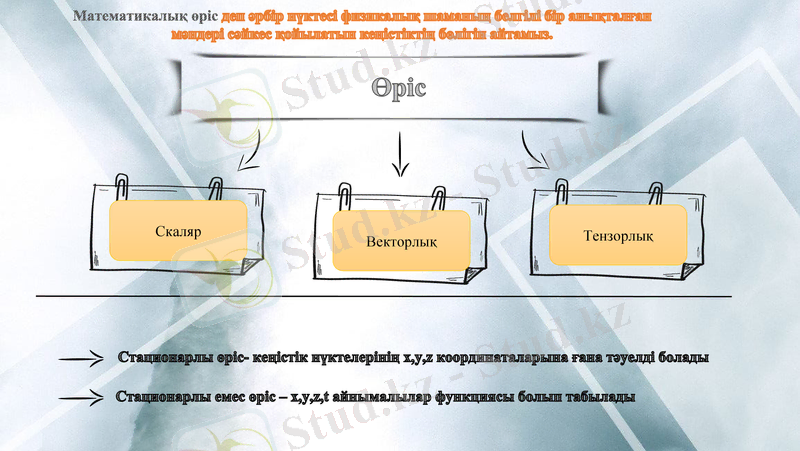
Өріс
Математикалық өріс деп әрбір нүктесі физикалық шаманың белгілі бір анықталған мәндері сәйкес қойылатын кеңістіктің бөлігін айтамыз.
Скаляр
Векторлық
Тензорлық
Стационарлы өріс- кеңістік нүктелерінің x, y, z координаталарына ғана тәуелді болады
Стационарлы емес өріс - x, y, z, t айнымалылар функциясы болып табылады

Скаляр өріс
Скалярлық өрістің градиенті
Кеңістіктің әрбір нүктесінде скаляр болатын функциямен сипатталатын физикалық өріс.

Векторлық өріс
Векторлық өріс - кеністіктің әрбір нүктесінде вектор болатын функциямен сипатталатын физикалық өріс.



НАЗАРЛАРЫҢЫЗҒА
РАХМЕТ!
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz