Теңсіздіктерді шешу
Презентация қосу
Оңтүстік Қазақстан Мемлекетік Педагогикалық Университеті
ПРЕЗЕНТАЦИЯ
Тақырыбы: Теңсіздіктерді шешу.
Тобы: 109-18.
Орындаған: Қожанова А.Ж.
Қабылдаған: Жетпісбаева Г.
Шымкент- 2021.
Жоспар:
• 1.Мектеп математика курсында теңсіздіктер тақырыбын
оқыту реті.
• 2. Теңсіздікті шешу және оның шешімдері.
• 3. Сызықтық теңсіздіктерді шешуге үйрету.
• 4. Теңсіздіктер жүйесі және бірілігі.
Әдетте мектепте «теңсіздік» тақырыбы бастауыш
сыныптан басталады. Олар санды теңсіздіктер.
3=3 = 3=5
Бұл - теңдік < Бұл - теңсіздік
=
- теңдік белгісі > - теңсіздік белгісі
3 тең 3-ке деп 3 тең емес 5-ке
оқылады. деп оқылады.
ТЕҢСІЗДІК
• ТЕҢСІЗДІК – ӨЗАРА ТЕҢ ЕМЕС
ЕКІ САН НЕМЕСЕ ӨРНЕКТІҢ
АРАСЫНДАҒЫ БАЙЛАНЫС.
>, < , ≥ , ≤ белгілері теңсіздік белгілері
деп аталады.
• а және b сандарын салыстырғанда a-b
айырмасы теріс сан болса ,а
L a b
0 1 2 3 4 5 6
> және < белгілері қарама – қарсы теңсіздік белгілері
> және > белгілері бірдей теңсіздік белгілері
< және < белгілері бірдей теңсіздік белгілері
деп аталады.
Сан аралықтары
-2 ≤ x ≤ 6
/////////////////////////////////////////////////////////
-2 6
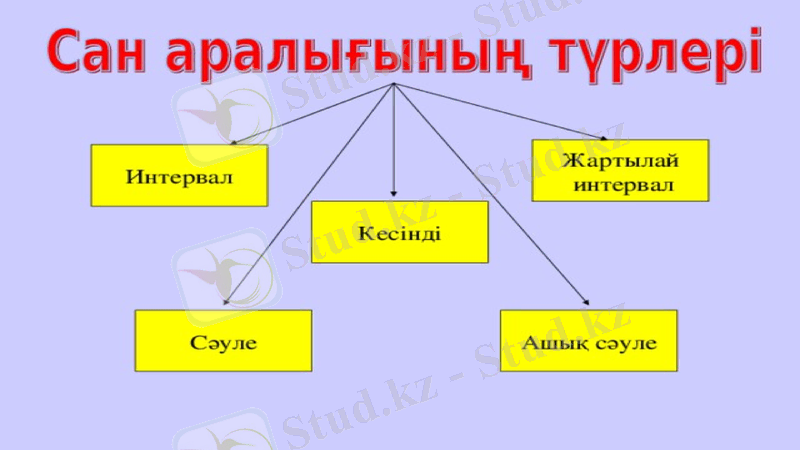
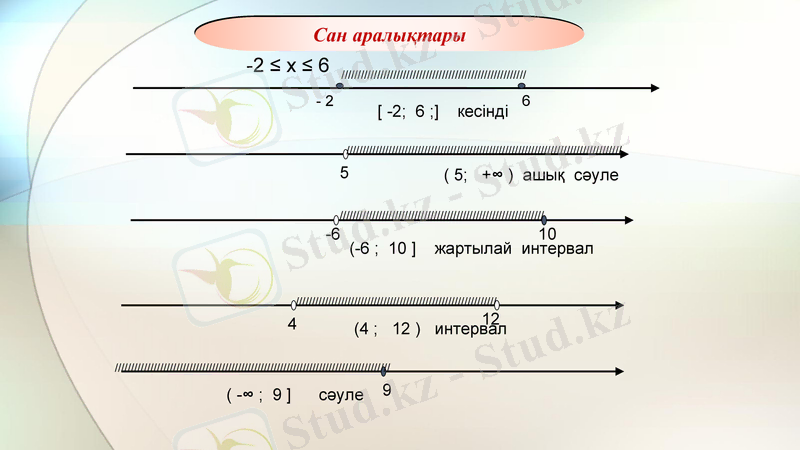
[ -2; 6 ;] кесінді
/////////////////////////////////////////////////////////////////////////////////////
5 ( 5; +∞ ) ашық сәуле
///////////////////////////////////////
////////////////////////
-6 10
(-6 ; 10 ] жартылай интервал
//////////////////////////////////////////////////////////////
4 12
(4 ; 12 ) интервал
/////////////////////////////////////////////////////////////////////////////////////
( -∞ ; 9 ] сәуле 9
• Мысалы :
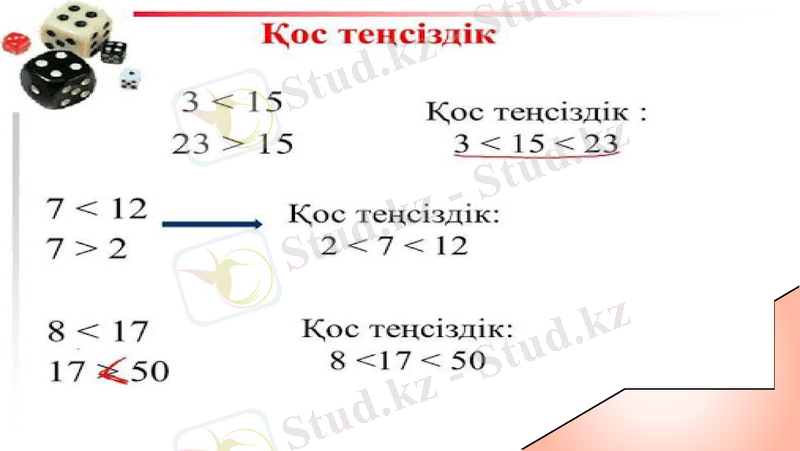
7>0 және 5 < 9 қарама – қарсы теңсіздік
белгілері бар санды теңсіздіктер
7 >5 және 9>2 - бірдей теңсіздік белгілері
бар санды теңсіздіктер.
< немесе > белгілерімен жазылса, қатаң
теңсіздіктер
≤ немесе ≥ белгілерімен жазылса ,қатаң емес
теңсіздіктер деп аталады.
• 1) a ≥ 5 теңсіздігі: «а саны 5 – тен артық немесе
тең» деп оқылса ,«а саны 5 – тен кем емес» деп те
оқылады.
• 2) b ≤ 4 теңсіздігі:«b саны 4 – тен кем немесе
тең» деп оқылса, « b саны 4 – тен артық емес» деп
те оқылады.
Теңсіздіктердің қасиеттері:
1). a > b, c > d болса онда a+c > c+d.
Мысалы 7 > 5, 3 > 2 соңдықтан 7+3 > 5+2.
2). a ≥ b, c ≥ d болса онда a+c ≥ c+d.
3). a > b болса онда –a < -c.
Мысалы 2>1, -2<-1.
4). a ≥ b болса онда –a ≤ -c.
5). a > b болсын, k саны оң болса онда k · a > k · b, k саны теріс болса
онда k · a < k · b.
Мысалы 3 > 2, 4·3 > 4·2, -4·3 < -4·2.
6). a ≥ b болсын, k саны оң болса онда k · a ≥ k · b, k саны теріс болса
онда k · a ≤ k · b.
Санды теңсіздіктерді көбейту
1) Санды теңсіздіктердің қасиетін пайдаланып, көбейткіш
теңсіздіктердің теңсіздік белгілерін бірдей етіп алу
керек.
2) Көбейткіш теңсіздіктерді мүшелеп көбейту керек
3) Көбейтінді теңсіздіктің теңсіздік белгісін көбейткіш
теңсіздіктердің теңсіздік белгісімен бірдей ету керек
Санды теңсіздіктерді бөлу
Бөлгіш теңсіздіктің мүшелерін оларға кері сандармен
алмастырып , теңсіздік белгісін қарама -қарсы белгіге
өзгерту керек.Бөлінгіш теңсіздік және бөлгіш теңсіздік
белгілерін бірдей теңсіздік белгісімен жазу керек .
Теңсіздік белгілері бірдей теңсіздіктерді мүшелеп
көбейту керек .
6( 3+5y) –(2+7y ) ≤ 5(4+3y)
18 +30y -- 2 –14y ≤ 20 + 15y
30y -14y -15y ≤ 20 – 16
//////////////////////////////
Жау: y ≤ 4 -∞ 4
Теңсіздіктің шешімдер жиыны координаталық
түзуде сәуле түрінде кескінделеді .
ортақ бөлімге келтіреміз ( о/б 14 )
7(4+у )-2(у+2 14(у+3) жақшаны ашсақ
28+7у-2у - 4 14у+42
7у -2у -14у 42+4 -28
-9у 18 ( -9 -ға бөлсек )
у -2 /////////////////////////////////////////////
-2
Жауабы : ( -2 ; +∞ )
Теңсіздіктің шешімдер жиыны координаталық түзуде ашық
сәуле түрінде кескінделеді .
Теңсіздіктер жүйесін шешу -
жүйеге қатысты барлық
теңсіздіктердің ортақ
шешімдерінің жиынын табу
Теңсіздіктер жүйесінің шешуі деп
теңсіздіктің әрқайсысын дұрыс
теңсіздікке айналдыратын
айнымалының мәнін атайды.
Шешу үшін жүйедегі теңсіздіктердің
әрқайсысын онымен мәндес теңсіздікке
түрлендіреміз:
Теңсіздіктердің табылған шешімдерін:
х>50 және х<70-ті бір координаталық
түзуге кескіндегенде,олардың ортақ
шешімдерінің жиыны (50;70) аралығы
болады.Себебі (50;+∞)∩(-∞;70)=(50;70)
₀ ₀
17< 4х-3 < 33 қос теңсіздігін теңсіздіктер жүйесі түрінде жазамыз:
Теңсіздіктердің әрқайсысын мәндес теңсіздікке
түрлендіргенде:
Осы мысалды қос теңсіздік түрінде де жазып,
шешуге болады.
17 < 4х-3 < 33
17+3 < 4х < 33+3
20 < 4х < 36
5<х<9
Теңсіздіктер жүйесінің шешімдер жиыны (5;9)
аралығы немесе
5<х<9
Сонымен, мектепте оқушылар осы мәліметтерді,
тақырыпшаларды білгенде ғана әрі қарай жоғары
сыныптарда ( 7-11 сынып) алып кете алады. Ол үшін
де функциялардың қасиеттерін ( квадраттық
функциялардың, тригонометриялық функциялардың,
логарифмдік функциялардың, көрсеткіштік
функциялардың, т.с.с. ) меңгеруі тиіс.
Сондықтан мұғалім әр кезеңде оқушылармен жақсы
жұмыс жасауы тиіс.
Зейін қойып
тыңдағандарыңызға
рахмет!!!
Ұқсас жұмыстар
Пәндер
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.
Ақпарат
Қосымша
Email: info@stud.kz