Рационал теңсіздіктерді интервал әдісімен шешу: анықтама, теорема және мысалдар



Сабақ тақырыбы: Рационал теңсіздік

Оқу мақсаты: 8. 2. 2. 9 рационал теңсіздіктерді шешу;

Сабақ мақсаттары: Оқушылар: Рационал теңсіздіктің анықтамасын тұжырымдайды; Рационал теңсіздіктерді шешеді, интервал әдісімен қолданып шешеді.

Бағалау критерийлері: Оқушылар оқу мақсаттарына жетеді, егер: рационал теңсіздіктің анықтамасын тұжырымдаса; рационал теңсіздіктерді интервал әдісін қолданып шешсе.

1. Функцияны анықтап оның анықталу облысын табу
2. Функцияны нөлмен салыстыру.
3. Функцияның нөлдерін табу
4. Теңдеудің түбірлерінің мәнін сан осіне белгілеп, сан осін интервалдарға бөлу.
5. Таңбасы теңсіздік таңбасына сәйкес интервалдарды жауап ретінде аламыз.
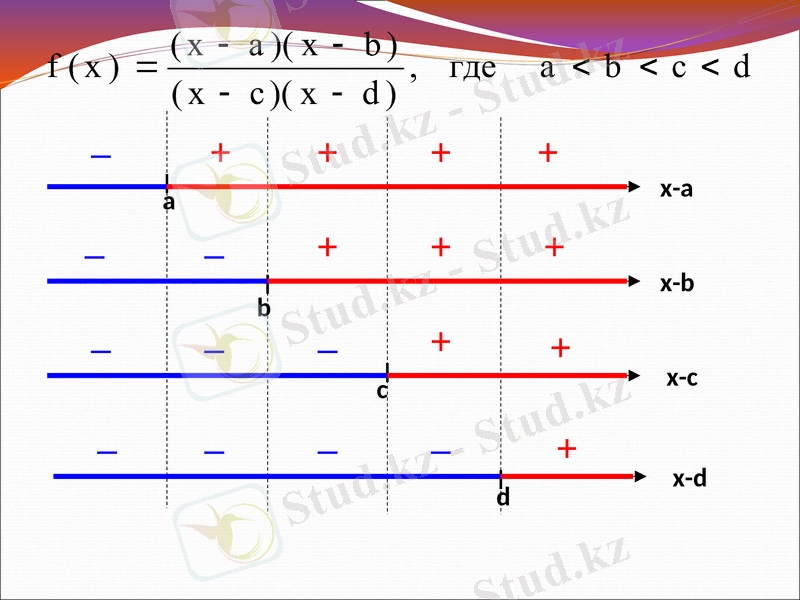
a
b
c
d
x-d
x-c
x-b
x-a
_
_
_
_
_
_
_
_
_
_
+
+
+
+
+
+
+
+
+
+

Теорема
Егер теңсіздіктің көбейткіші жұп дәрежелі болса, онда функция осы көбейткіштің нөлінен оң жағынан сол жағына өткенде таңбасы сақталады.

Мысал 1
Теңсіздікті шешейік: (х-2) (х-3) (х-4) >0.
ОХ осінде 2; 3; 4 нүктелерін белгілейік
(4; +∞) ; (3; 4) ; (2; 3) ; (-∞; 2) интервалдардың үстіне кезектесіп «+»; «-» таңбаларын жазамыз.
Жауабы:(2; 3) U(4; +∞)
+
-
+
-

Мысал 2
Теңсіздікті шешейік: (2-х) (х2-4х+3) (х+1) >0
Квадрат үшмүшені көбейткіштерге жіктейік:
(2-х) (х-3) (х-1) (х+1) >0
Екі жағын -1-ге көбейтейік
(х-(-1) ) (х-1) (х-2) (х-3) <0
-1; 1; 2; 3 нүктелерін белгілейік
Жауабы:(-1; 1) U(2; 3)
+
-
+
-
+

Мысал 3
Теңсіздікті шешейік:(х-1) (х-3) (х2+х+1) <0
х2+х+1 тек оң мәндерді қабылдайды (D<0) .
(х-1) (х-3) <0
Интервал әдісімен шешсек:
Жауабы:(1; 3)
+
-
+

Мысал 4
Теңсіздікті шешейік:(х-1) 3(х-2) 2(х-3) 4(х-4) <0
Мұндай теңсіздіктерді шешу үшін жалпы интервалдар әдісін қолданады:
1; 2; 3; 4 нүктелерін белгілейік,
А(х) = (х-1) 3(х-2) 2(х-3) 4(х-4) көпмүшенің әрбір интвервалда
Таңбаларын анықтаймыз:
Жауабы:(1; 2) U (2; 3) U(3; 4) .
+
-
-
+
-

1. Теңсіздікті шешіңдер: -х²+7х-12≥0
у=-х²+7х-12 функцияны қарастырайық
а=-1, параболаның тармақтары төмен бағытталған.
-х²+7х-12=0 теңдеуді шешеміз
D=49-48=1
х₁=(-7+1) :(-2) ; х₂=(-7-1) :(-2)
х₁=3; х₂= 4
3
4
Жауабы: хЄ[3; 4]

2. Теңсіздікті шешіңдер х²-4>0
у=х²-4,
а=1- парабола тармақтары жоғары бағытталған;
х²-4=0
х²=4
х=±2
Параболаның сұлбасын саламыз
Жауабы: хЄ(-∞; -2) U(2; +∞)
-2
2

Скачано с www. znanio. ru
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz