Нақты сандар мен функциялардың негізгі ұғымдары



Жиындар теориясының қарапайым ұғымдары




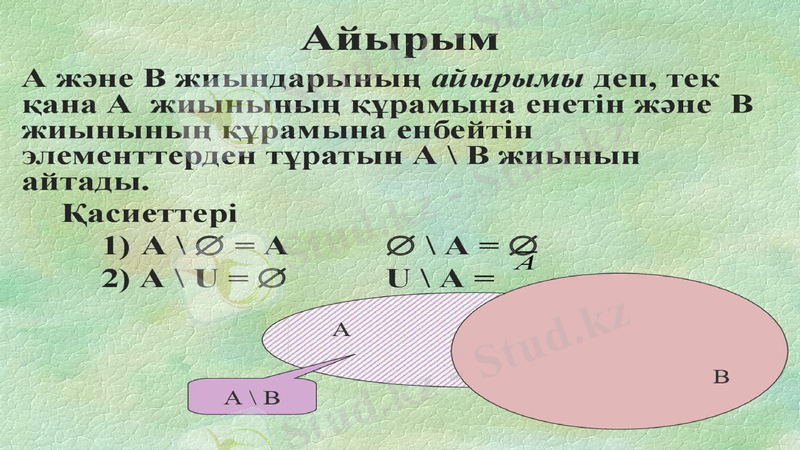

Нақты сандар жиыны
1. Натурал сандар
Натурал сандар деп мына сандарды атаймыз 0, 1, 2, 3, 4, …
Барлық натурал сандар жиының N символымен белгіленеді. Белгілі бір a санының натурал сан екенің көрсету үшін a ∈ N деп белгілейміз. Мысалы 1 ∈ N, 5 ∈ N, 3 ∈ N.
2. Бүтін сандар
Бүтін сандар деп оң және теріс таңбасымен алынған барлық натурал сандар жиынынан құралған сандар жиының атаймыз.
Яғни бүтін сандар 0, 1, 2, 3, 4, … және -1, -2, -3, -4, … сандар жиындарының бірігуінен құралған. Бүтін сандар жиының P символымен белгілейміз.

3. Рационал сандар
Рационал сандар деп рационал сандар (a ∈ P, b ∈ P, b ≠ 0) сандарын атаймыз. Рационал сандар жиының R деп белгілейміз.
Кез келген бүтін c саны рационал жиынына еңеді да, яғни рационал саны да болып табылады. Өйткені рационал сан, соңдықтан P ⊆ R.
4. Иррационал сандар
Иррационал сан деп π = 3, 141592… немесе иррационал сандар = 1, 4… сандары тәрізді бөлшек бөлігі шексіз, периодты емес цифрлардан құралған сандарды атаймыз.
Иррационал сандар жиының Q деп белгілейміз.

5. Нақты сандар
Нақты сандар жиыны деп барлық- натурал, бүтін, рационал және иррационал сандардан құралған сандар жиының атаймыз. Және бұл жиынды Z әрпімен белгілейміз.
Абсолютті шама, немесе модуль - нақты санының төмендегідей жолмен анықталатын теріс емес сан. Белгіленуі - x
Нақты санның абсолюттік шамасы:
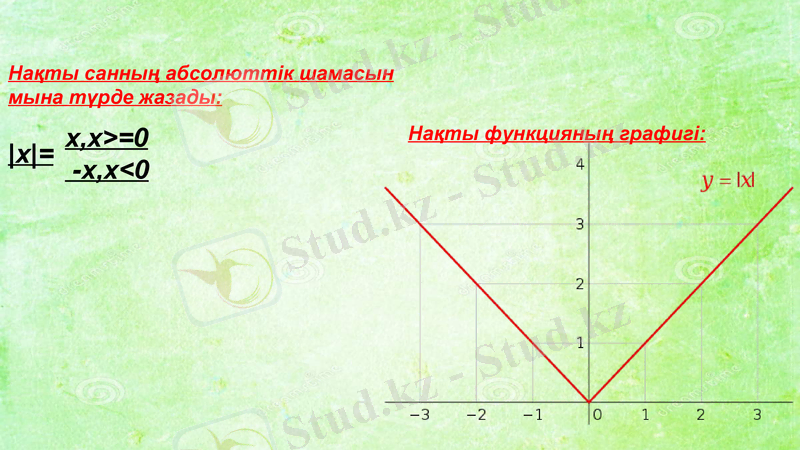
x, x>=0
-x, x<0
х=
Нақты санның абсолюттік шамасын
мына түрде жазады:
Нақты функцияның графигі:
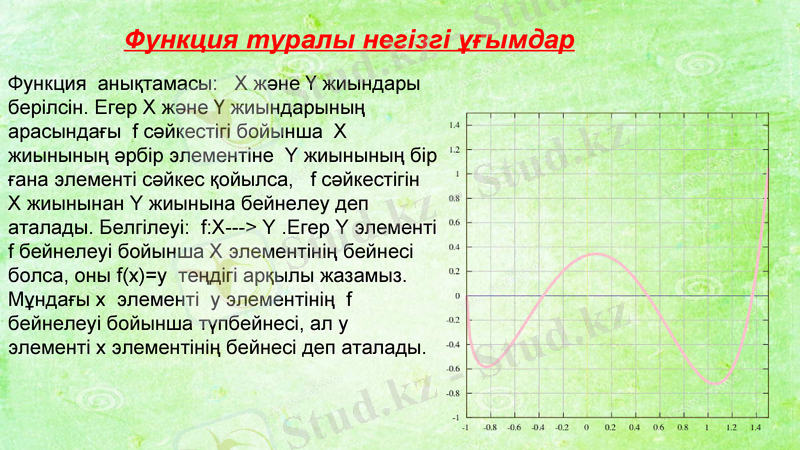
Функция туралы негізгі ұғымдар
Функция анықтамасы: Х және Ү жиындары берілсін. Егер Х және Ү жиындарының арасындағы f сәйкестігі бойынша X жиынының әрбір элементіне Y жиынының бір ғана элементі сәйкес қойылса, f сәйкестігін X жиынынан Y жиынына бейнелеу деп аталады. Белгілеуі: f:X---> Y . Егер Y элементі f бейнелеуі бойынша X элементінің бейнесі болса, оны f(x) =y теңдігі арқылы жазамыз. Мұндағы x элементі y элементінің f бейнелеуі бойынша түпбейнесі, ал y элементі x элементінің бейнесі деп аталады.

1. Сан функциясы, оның анықталу облысы мен өзгеру облысы
Анықтама. Егер белгілі бір ереже (заң) бойынша Х жиынын құрастыратын әрбір нақты х санына У жиынын құрастыратын сандардың біреуі у ғана сәйкес келсе, онда Х жиынында бір мәнді y=f(x) функциясы берілген дейді және осылайша анықталған функцияны сан функциясы деп айтады.
Аргументтің жеке мәндеріне сәйкес y=f(x) функциясының мәндерін табу үшін, функциядағы аргумент x -тің орнына берілген мәнді қойып есептеу керек. Оны былай белгілеп жазады:
y0=f(x) 0=f(x) x=x0

2. Функция графигі
Анықтама. y=f(x) функциясының графигі деп, координаталары осы теңдеуді қанағаттандыратын жазықтықтағы жиынын айтамыз. Ал, y=f(x) осы графиктің теңдеуі делінеді. Жоғарыда көрсетілгендей функцияның графигі жазықтықтағы сызық бола бермейді. Белгілі нүктелердің жиыны болғанымен, ол нүктелер бір сызық құрауы шарт емес. График - функцияның геометриялық кескіні, мағынасы болады. Ол көп жағдайларда функцияның мағынасын, қасиеттерін көрнекті түсінуге көмектеседі.

3. функциялардың берілу тәсілдері.
f(x) -функциясының берілуі аргумент x-тің әрбір мәніне сәйкес келетін f(x) функциясы мәнін көрсету болып табылады. Функцияның негізгі үш берілу тәсілдерін келтірейік.
1) Аналитикалық тәсіл
2) Кестелік тәсіл
3) Графиктік тәсіл

Аналитикалық тәсіл. Бұл тәсілде айнымалы шамалар арасындағы тәуелділік функция мәнін алу үшін аргумент мәніне қандай амалдар орындау керек екенін көрсететін формула жәрдемімен беріледі.
Функцияның кестелік тәсілмен берілуі. Бұл тәсілде аргументтің жеке мәндеріне сәйкес тәуелді айнымалының мәндері кесте түрінде беріледі, яғни х пен у айнымалылары арасындағы сәйкестік ережесі х-тің жеке-жеке мәндеріне сәйкес келетін у-тің мәндері беріліп, осы мәндерден кесте құрылады
Функция берілуінің графиктік тәсілі, әсіресе х пен у айнымалылары арасындағы тәуелділік график түрінде берілетін физикалық өлшеулер практикасында жиі қолданылады. Көп жағдайларда, мұндай графиктер өзі жазатын құралдар жәрдемімен сызылады. Атап айтқанда, әртүрлі биіктіктегі атмосфера қысымын өлшеу үшін өзі жазатын құрал - барограф қолданылады.

Кері функция
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz