Біртекті және біртекті емес коэфиценнті тұрақты екінші ретті сызықтық дифференциалдық теңдеулер

Презентация қосу

«Оңтүстік Қазақстан Медициналық Академиясы» АҚ
Медициналық биофизика және ақпараттық технологиялар кафедрасы

Тақырып: Біртекті және біртекті емес
коэфиценнті тұрақты екінші ретті сызықтық
дифференциалдық теңдеулер.

Орындаған: Дүйсенбай Алмасхан
Топ: ФӨТҚАБ 02-21 А
Қабылдаған: Иманбаева Марал
Жоспары

1 Кіріспе

2 Негізгі бөлім

3 Есеп шығару мысалдары

4 Қорытынды
Кіріспе

Дифференциялдық теңдеулер арасында ең
жиі кездесетіні екінші реттік
дифференциялдық теңдеулер. Бұл теңдеудің
ішінде міндетті түрде y’’ екінші туынды болуы
қажет. Айта кету керек, кейбір элементтер
x, y, y’
екінші реттік теңдеуде болуы міндетті түрде
емес.
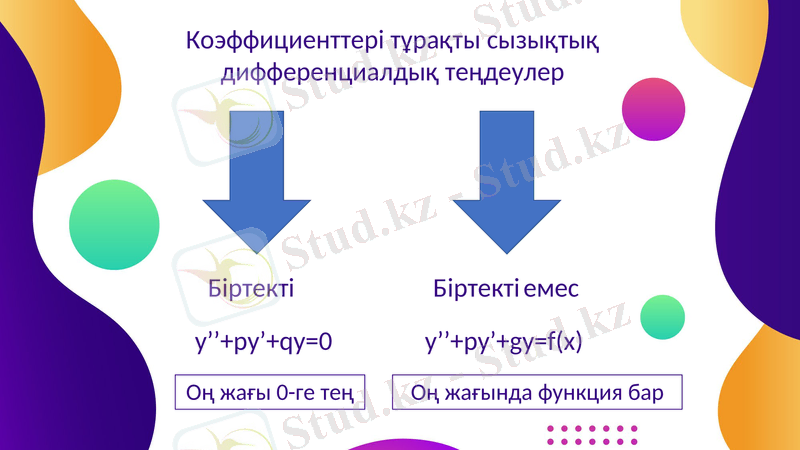
Коэффициенттері тұрақты сызықтық
дифференциалдық теңдеулер

Біртекті Біртекті емес
y’’+py’+qy=0 y’’+py’+gy=f(x)
Оң жағы 0-ге тең Оң жағында функция бар
Коэффициенттері тұрақты біртекті
сызықтық дифференциалдық теңдеулер
y’’+py’+qy=0

түріндегі теңдеуі p және q – тұрақты сандар болғанда
коэффициенттері тұрақты біртекті екінші ретті сызықтық
дифференциалдық теңдеу деп аталады.
Бұл теңдеуді шеші үшін y’’-ті k2-пен, y’-ті k-мен, y-ті 1-мен
алмастыру арқылы осы теңдеудің сипаттамалық (не
характеристикалық) теңдеуін аламыз
k2+pk+q=0
Сипаттамалық теңдеуді шешкенде үш түрлі жағдайдың
болатынын білеміз:
1. Сипаттамалық теңдеудің түбірлері D>0 болғанда k1≠k2 – нақты
және өзара тең емес болса, онда теңдеудің жалпы шешімі:
y=C1ek1x+C2ek2x
2. Сипаттамалық теңдеудің түбірлері D=0 болғанда k1=k2=k – нақты
және өзара тең болса, онда теңдеудің жалпы шешімі:
y=exk(C1+C2x)
3. Сипаттамалық теңдеудің түбірлері D<0 болғанда k1, k2 – түйіндес
комплекс сандар, k1,2=α±βi болса, онда теңдеудің жалпы шешімі:
y=eαx(C1cosβx+C2sinβx)
Коэффициенттері тұрақты біртекті емес
сызықтық дифференциалдық теңдеулер
y’’+py’+gy=f(x)

теңдеуі коэффициенттері тұрақты біртекіті емес сызықтық
диффиренциалдық теңдеу деп аталады.
Жалпы шешімі y=y0+ŷ формуласымен табылады, мұндағы y0 -
y’’+py’+qy=0 теңдеуінің жалпы шешімі, ал ŷ функциясы
y’’+py’+gy=f(x) теңдеуінің дара шешімі, ол теңдеудің оң
жағындағы f(x) функциясының берілі түріне байланысты.
f(x) функциясы төмендегідей берілсін:
Қорытынды

Бұл өзіндік жұмыста коэффициенттері тұрақты сызықтық
дифференциалдық теңдеулердің екі түрі бар екенін білдік.
Олардың формулаларын және шығару жолдарын қарастырдық.
Есеп шығару мысалдары
1-мысал: f(x)=9x-3 функциясының экстремумын табу
Шешуі:
1) Функцияның туындысын табамыз: f’(x)=9
2) Cындық нүктелерді табамыз: 9≠0 Сындық нүктелер жоқ.
3) Бұл функция сызықтық функция болып табылады, сондықтан
экстремум нүктелері жоқ.
Жауабы: f(x)=9x-3 функциясының экстремумы жоқ.

Ұқсас жұмыстар

Дифференциалдық теңдеулер

Айнымалы коэффициенттерімен дербес туындылы дифференциалдық теңдеулерді математикалық Maple пакеттерінде зерттеу және келтіру

БІРТЕКТЕС СЫЗЫҚТЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУДІҢ ФУНДАМЕНТАЛДЫ ЖҮЙЕСІ

ЕРКІН ЕМЕС МАТЕРЯЛЫҚ НҮКТЕ ҚОЗҒАЛЫСЫНЫҢ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРІ ЖӘНЕ ОНЫ НҮКТЕ ДИНАМИКАСЫНЫҢ НЕГІЗГІ ЕСЕПТЕРІН ШЕШУ ҮШІН ҚОЛДАНУ

Процестердің ұқсастық түрлері

Каноникалық теңдеулер

Өткізгіштердің кедергісі

Бейсызықты автоматты басқару жүйелері

Модельдеу объектісі

Матрицалық, экономикалық, математикалық модельдеу

Пәндер