Мектеп-ЖОО жүйесінде дискретті математика элементтерін оқыту әдістемесі



Ө. А. Байқоңыров aтындaғы Жезказған университеті
Гуманитарлық педагогтік институты
Жаратылыстану кафедрасы
ДИПЛОМДЫҚ ЖҰМЫС
«Мектептегі дискретті математика элементтерін оқыту әдістемесі»
Орындaғaн: инф-17-1т. ст. Мухтар. М
Ғылыми жетекшісі: ф. -м. ғ. д., профессор Кудайкулов А.

Жиырма бірінші ғасыр түбегейлі жаңа экономика мен ақпараттық технологиялар жағдайында басталды, бұл білім беруді жаңғыртуды қажет етеді. Білім беруді жаңғыртудың басты мақсаты оның сапасын арттыру болып табылады.
Өткен ғасырда математикада үлкен өзгерістер болды, бұл оны талдау, зерттеу және болжаудың қуатты құралдарына айналдырды.
Сондықтан білім сапасын арттыру үшін мамандыққа байланысты математиканы оқыту мазмұнын оңтайландыру қажет.
Компьютерлердегі есептеу процесі дискретті болғандықтан, ДM-нің басты ерекшелігі-классикалық математикаға тән шекті ауысу мен үздіксіздіктің болмауы.
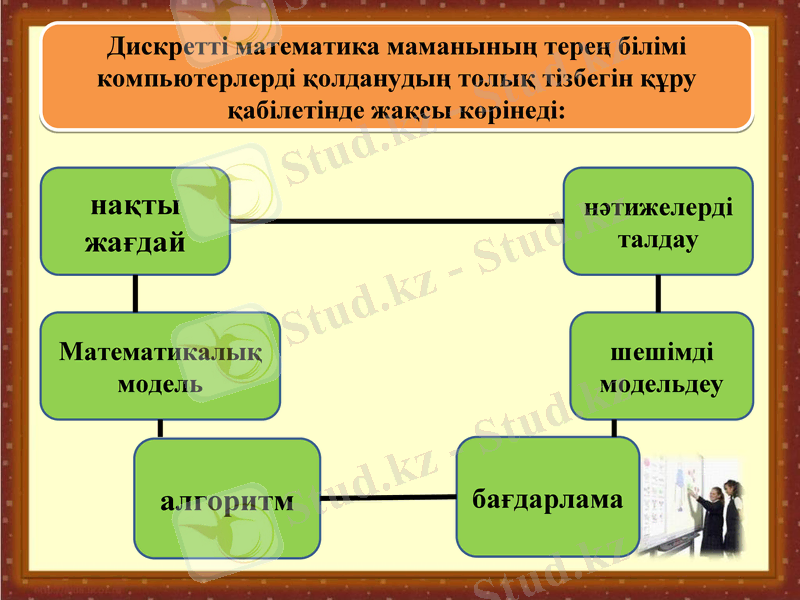
Дискретті математика маманының терең білімі компьютерлерді қолданудың толық тізбегін құру қабілетінде жақсы көрінеді:
нақты жағдай
Математикалық модель
алгоритм
бағдарлама
шешімді модельдеу
нәтижелерді талдау

Компьютерлерді пайдалану тізбегі тұрғысынан Л. Д. Кудрявцев қазіргі математикалық білімнің алдында тұрған негізгі мақсаттарды сипаттайды:
математикалық есептерді қоя білуге үйрету (басқаша айтқанда - нақты жағдайды, есептерді математикалық тілге аударуды үйрету),
математикалық модельдерді құру,
есептерді шешудің қолайлы математикалық әдісі мен алгоритмін таңдау,
жүргізілген математикалық талдау негізінде практикалық қорытындылар жасау.

Зерттеу мақсаты - дискретті математиканың пәндік мазмұнын әдіснамалық талдау арқылы "мектеп-ЖОО" жүйесінде дискретті математиканы оқыту заңдылықтарын анықтау; оларды анықтайтын факторларды бағалау және талдау; мектеп пен ЖОО-да осындай оқытудың теориялық негізделген және эксперименттік тексерілген әдістемелік жүйесін әзірлеу.
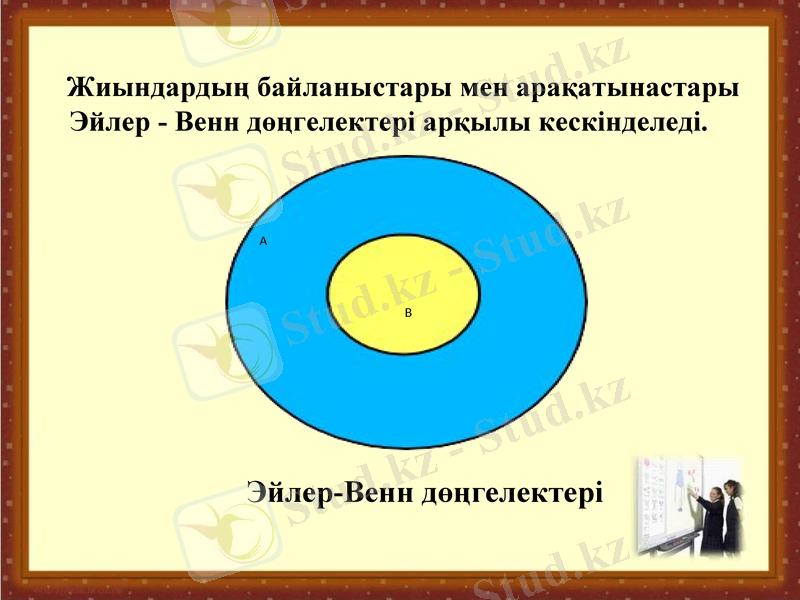
Жиындардың байланыстары мен арақатынастары Эйлер - Венн дөңгелектері арқылы кескінделеді.
Эйлер-Венн дөңгелектері

Жиын деп анықталған нысандардың бірге топтасуын айтады. Жиынның элементі деп жиынның жекешенысанын айтады. Бос жиын ∅ деп, құрамында бір де бір элемент жоқ жиынды айтады.
Әмбебап жиын (универсум) U деп, қарастырылған барлық қолданылатын элементтер жиынын айтады.
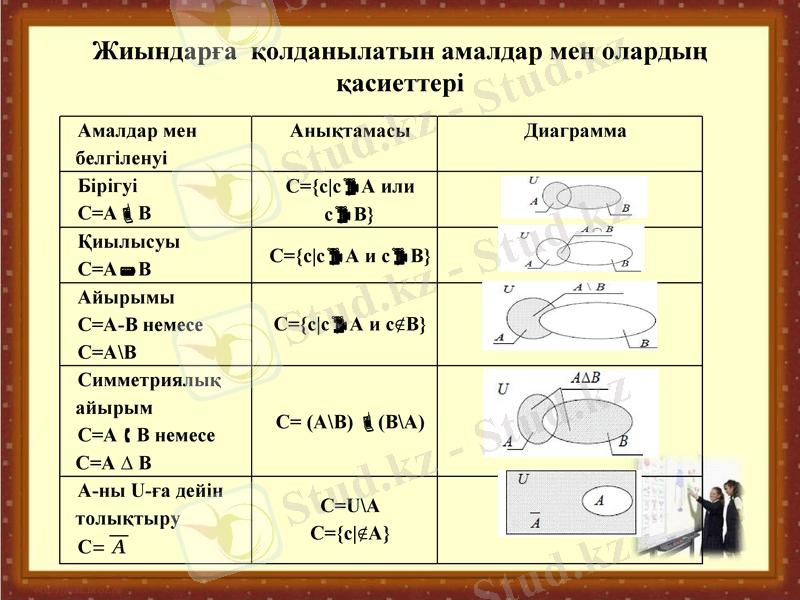
Жиындарға қолданылатын амалдар мен олардың қасиеттері
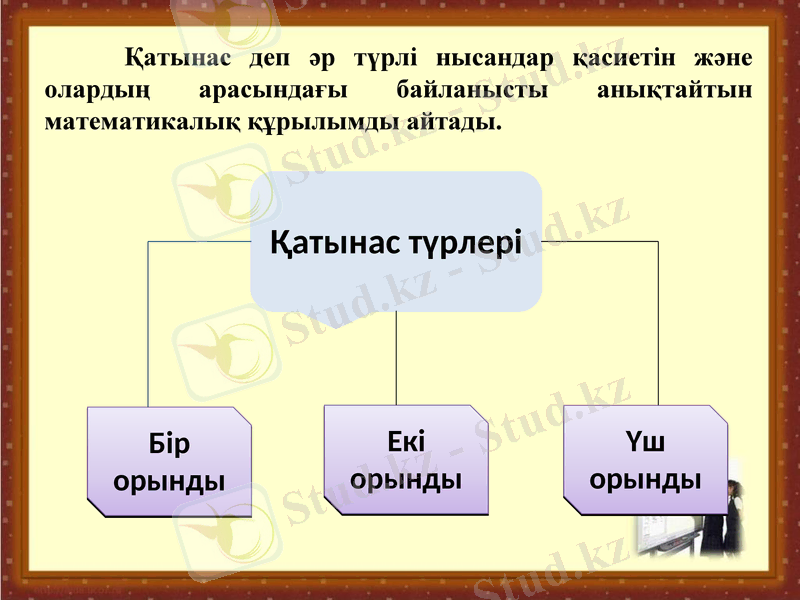
Қатынас деп әр түрлі нысандар қасиетін және олардың арасындағы байланысты анықтайтын математикалық құрылымды айтады.
Бір орынды
Екі орынды
Үш орынды
Қатынас түрлері
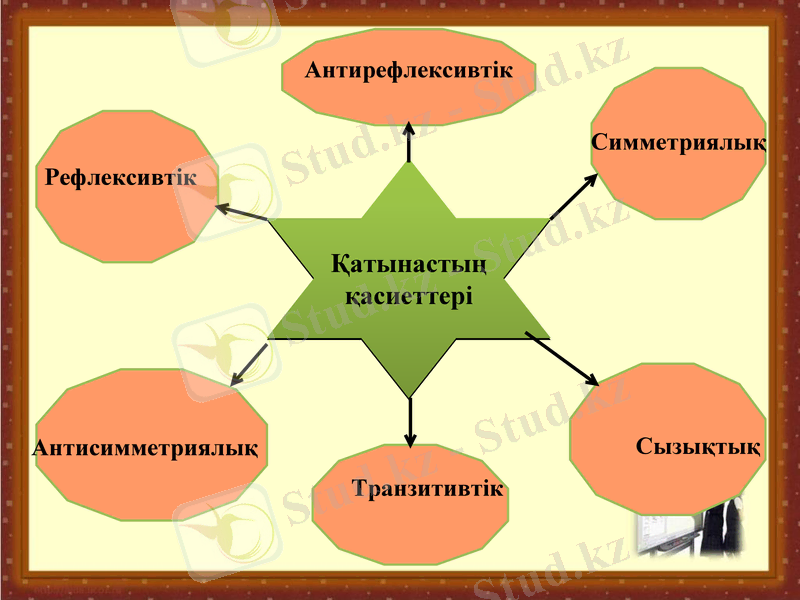
Қатынастың қасиеттері
Антирефлексивтік
Рефлексивтік
Симметриялық
Антисимметриялық
Транзитивтік
Сызықтық

Графтар
Егер графтың барлық қабырғалары бағытталмаған болса, онда ол бағытталмаған граф деп, ал егер графтың барлық қабырғалары бағытталған болса, онда ол бағытталған граф деп аталады.
Егер графта бағытталған және бағытталмаған да қабырғалар болса, ол аралас граф деп аталады.
Егер граф қабырғалары шыңдардың реттелген жұбымен анықталса, онда оны бағытталған қабырға немесе доға деп атайды (сызбада бағытталған қабырғаға оның бағытын анықтайтын стрелкалар қойылады) .

Графтың қасиеттері
Егер екі шың екі немесе одан да көп қабырғалармен қосылса, онда мұндай қабырғалар параллельді деп аталады (мысалы, қабырғалар е4 және е5) .
Егер қабырғаның басы мен соңы бір жерден шықса, онда мұндай қабырға ілмек (петля) деп аталады(мысалы, қабырға e7) . Ілмексіз және параллельді қабырғаларсыз графтар қарапайым деп аталады.

Комбинаторика элементтері
Саны шектеулі элементтерден әр түрлі комбинациялар құрастыруға және белгілі бір ереже бойынша құрастырылған барлық мүмкін комбинациялар санын есептеуге тура келетін жағдайлар жиі кездесіп отырады. Мұндай есептер комбинаторлық есептер, ал оларды шешумен шұғылданатын математика бөлімі комбинаторика деп аталады.
Комбинаторикада тек шектеулі жиындар ғана қарастырылады. Математиканың бұл бөлімінің ықтималдық теориясында, басқарушы жүйелер теориясында есептеу машиналарында және ғылым мен техниканың басқа да көптеген салаларында маңызы зор.

Комбинаторика мынандай жағдайларға байланысты есептерді қарастырады
берілген қасиеттерге ие болатын қанша элемент болатындығын анықтау;
берілген қасиеттерге ие болатын барлық элементтердің алгоритмін құру
қандай да бір қасиеті бойынша берілген элементтер ішінен ең жақсысын іріктеп алу.
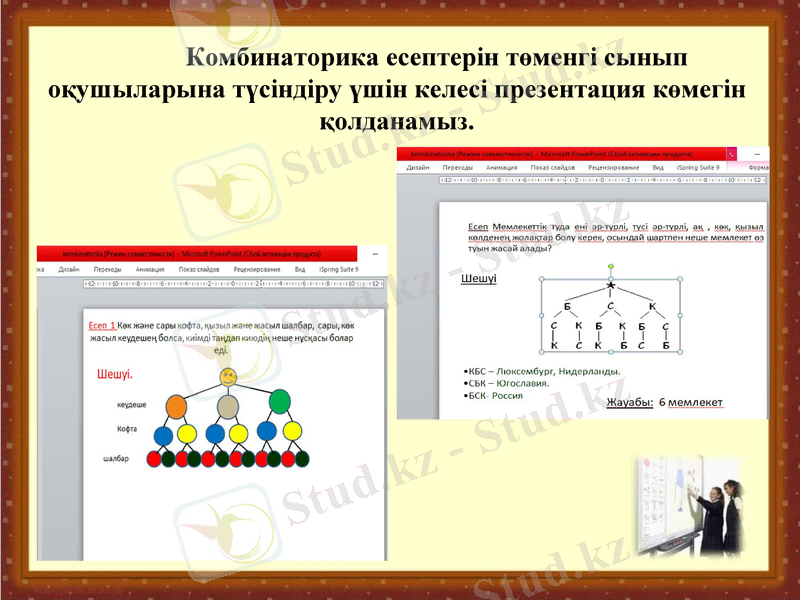
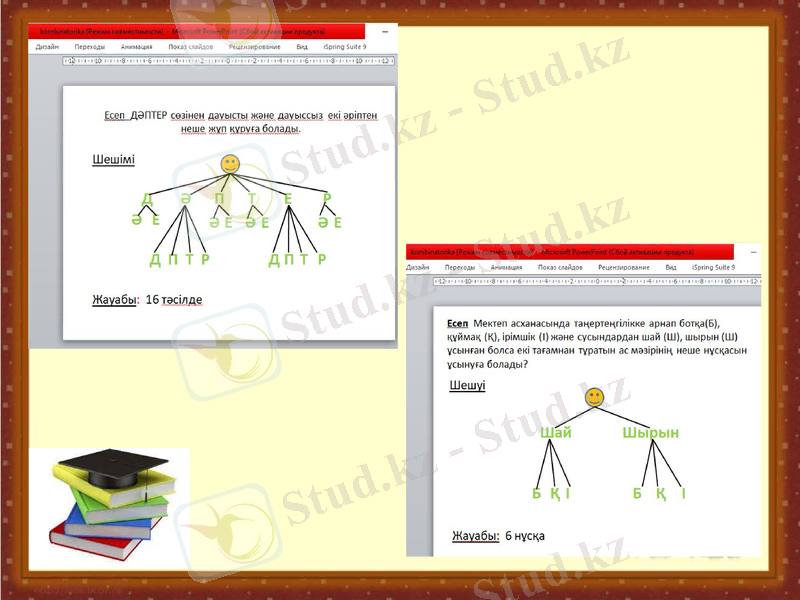
Комбинаторика есептерін төменгі сынып оқушыларына түсіндіру үшін келесі презентация көмегін қолданамыз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz