Материалдық нүкте мен қатты дененің кинематикасы



Материалдық нүктенің кинематикасы
Орындаған: Шадиярова Ырысгүл Бағытқызы
Мамандық: Математика және физика пәнінің мұғалімі. 2 жылдық, 1-курс

Кинематика - теориялық механика пәнінің кинематика
бөлімінде, дене қозғалысы оны қозғалысқа келтіретін күштерді
ескермей қарастырылады да және дене қозғалысының
геометриялық параметрлері (траектория, жылдамдық, үдеу)
анықталады.
Нүкте кинематикасы - екі мәселе қарастырады:
Кинематика
Нүкте кинематикасы
Қатты дене кинематикасы

1. Нүктенің қозғалыс теңдеуі - қозғалыстағы нүктенің берілген санақ жүйесіне қарағандағы орны уақытқа тәуелді теңдеулер арқылы беріледі.
Осы теңдеулер арқылы қозғалыстағы нүктенің барлық кинематикалық сипаттамаларын (траекториясын, жылдамдығын, үдеуін) табу;
2. Қозғалыс траекториясы - қозғалып бара жатқан нүктенің кеңістіктегі геометриялық орындарын қосатын үздіксіз сызық.
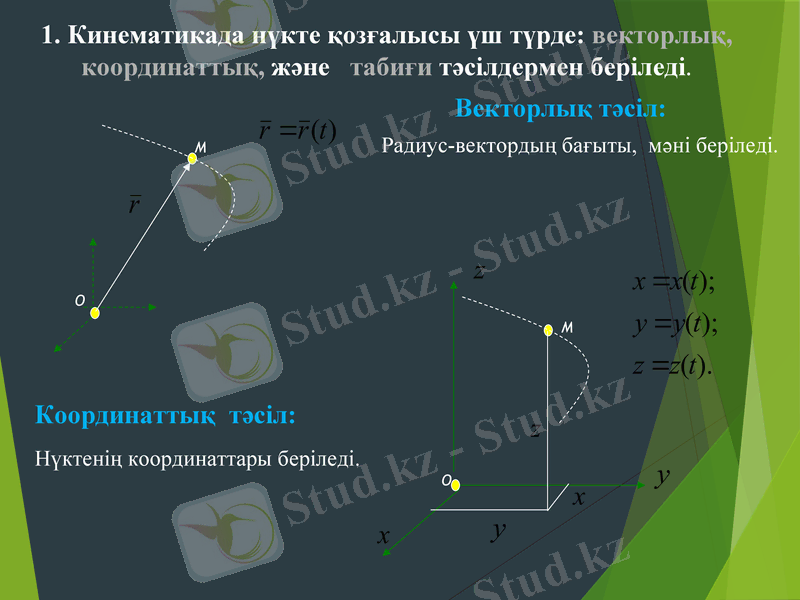
1. Кинематикада нүкте қозғалысы үш түрде: векторлық, координаттық, және табиғи тәсілдермен беріледі.
Векторлық тәсіл:
Координаттық тәсіл:
Нүктенің координаттары беріледі.
Радиус-вектордың бағыты, мәні беріледі.

Табиғи тәсіл:
Нүктенің қозғалыс теңдеуі мен траекториясы беріледі.

2. Қозғалыстың траекториясын анықтау үшін координаттық тәсілдің теңдеулерінен уақытты жою керек:
Барлық үш тәсіл де бір-біріне эквивалентті және бір-бірімен байланысты.
Векторлық пен координаттық:
Соңғы екі теңдеу қозғалыстың траекториясын сипаттайды.

Мысал:
Соңғы екі теңдеу радиусы R болатын цилиндр, биіктігі с-ға тең, z өсіне параллель болады. Сонда нүктенің траекториясы радиусы R-ға тең шеңбер

Нүкте жылдамдығы - нүктенің бірлік уақытта орын ауыстыру тездігін (шапшаңдығын) анықтайтын физикалық шама.
Нүктенің жылдамдығын анықтаудың үш түрі:
Векторлық тәсіл: Нүктенің екі түрлі уақыттағы t және t1= t + t жағдайын салыстырамыз:
t уақыттағы орта жылдамдық,
MM1 хорда бойымен бағытталған
t 0 дағы шек:

t уақытындағы жылдамдық векторы, ол траекторияға жанама бағытталған.
Радиуса-вектор мен координаттардың байланысы:
Координаттық тәсіл:
Векторлық тәсілді жылдамдықты анықтау үшін қолданамыз:

Табиғи тәсіл:
Жылдамдық векторы:
Жанамаға проекциясы:
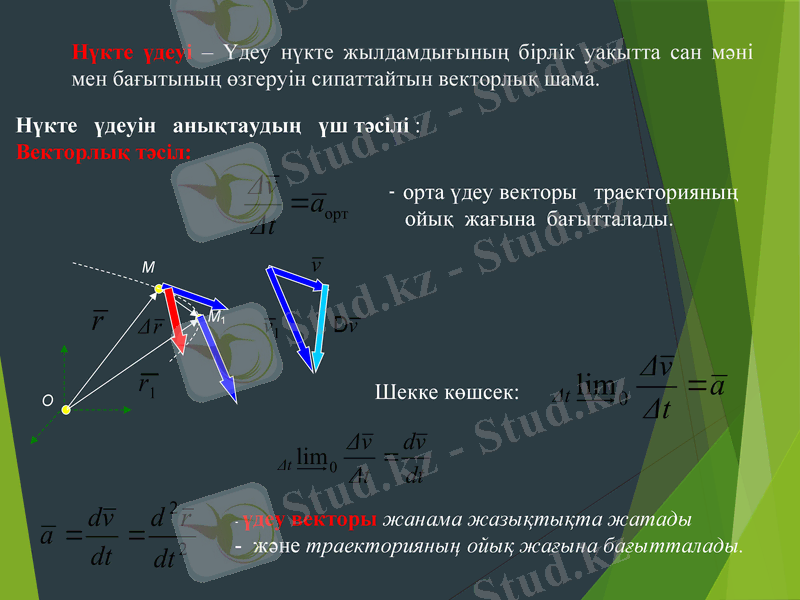
Нүкте үдеуі - Үдеу нүкте жылдамдығының бірлік уақытта сан мәні мен бағытының өзгеруін сипаттайтын векторлық шама.
Нүкте үдеуін анықтаудың үш тәсілі :
Векторлық тәсіл:
орта үдеу векторы траекторияның
ойық жағына бағытталады.
Шекке көшсек:
үдеу векторы жанама жазықтықта жатады
және траекторияның ойық жағына бағытталады.
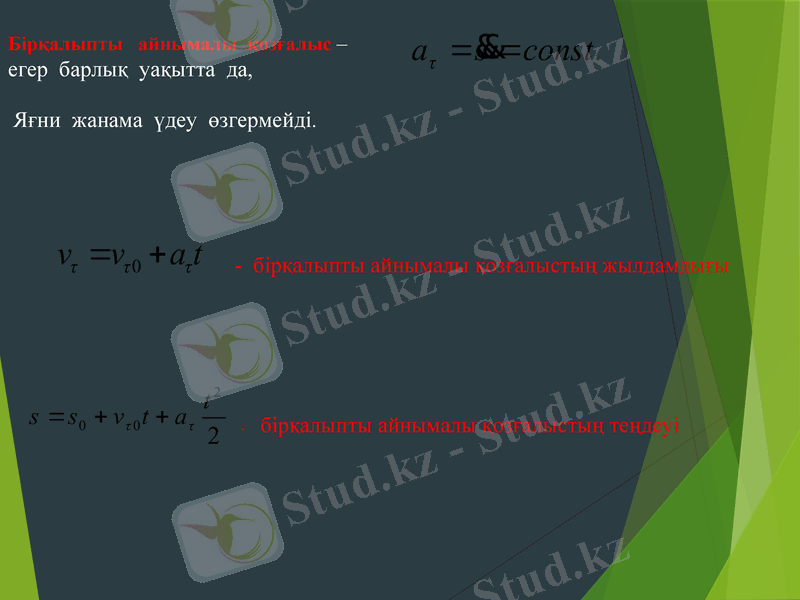
Бірқалыпты айнымалы қозғалыс -
егер барлық уақытта да,
Яғни жанама үдеу өзгермейді.
бірқалыпты айнымалы қозғалыстың жылдамдығы
бірқалыпты айнымалы қозғалыстың теңдеуі

Қатты дене кинематикасы - қозғалыстың бес түрі:
1. Ілгерілемелі (ползун, насостың поршені, паравоздың дөңгелектері(спарник), түзу жолмен жүру, лифтің кабинасы, купенің есігі) .
2. Айналмалы (маховик, кривошип, кәдімгі есік) .
3. Жазықпараллеь немесе жазық (шатун, локомотивтің дөңгелегі) .
4. Сфералық (гироскоп) .
5. Қозғалыстың жалпы жағдайы немесе еркін ұшу (оқ, тас, аспан денесі)
Ілгерілемелі қозғалыс - Қатты дененің онымен өзгерместей болып бекітілген түзуі өзінің бастапқы қалпына параллель қалып отыратын қозғалысы.
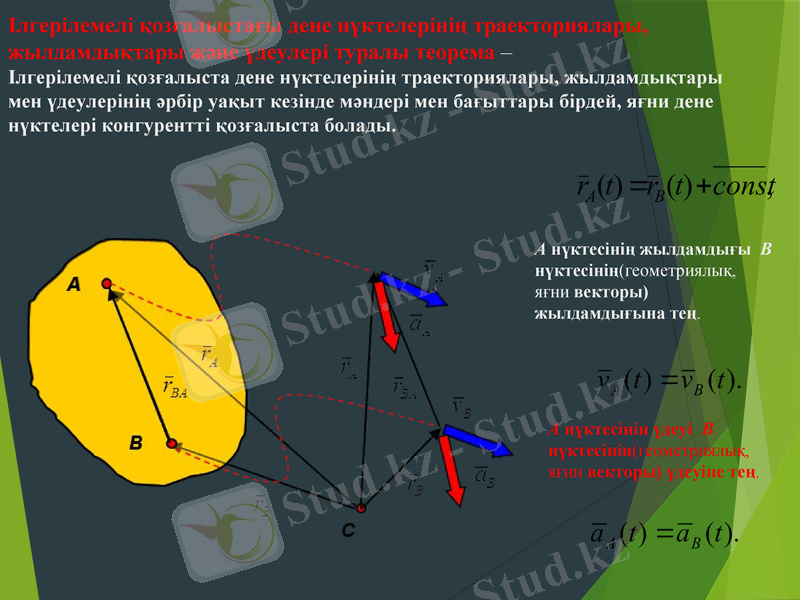
Ілгерілемелі қозғалыстағы дене нүктелерінің траекториялары,
жылдамдықтары және үдеулері туралы теорема -
Ілгерілемелі қозғалыста дене нүктелерінің траекториялары, жылдамдықтары
мен үдеулерінің әрбір уақыт кезінде мәндері мен бағыттары бірдей, яғни дене
нүктелері конгурентті қозғалыста болады.
A нүктесінің жылдамдығы B нүктесінің(геометриялық, яғни векторы) жылдамдығына тең.
A нүктесінің үдеуі B нүктесінің(геометриялық, яғни векторы) үдеуіне тең.

Сонымен, ілгерілемелі қозғалыстың барлық кинематикалық сипаттамаларын( траектория, жылдамдық және үдеу) оның жалғыз ғана нүктесінің қозғалысы арқылы анықтауға болады.
Қатты дененің айналмалы қозғалысы - Егер қозғалыстағы дененің кем дегенде екі нүктесі қозғалмайтын болса, онда мұндай дене тұрақты өстен айналмалы қозғалыста болады.
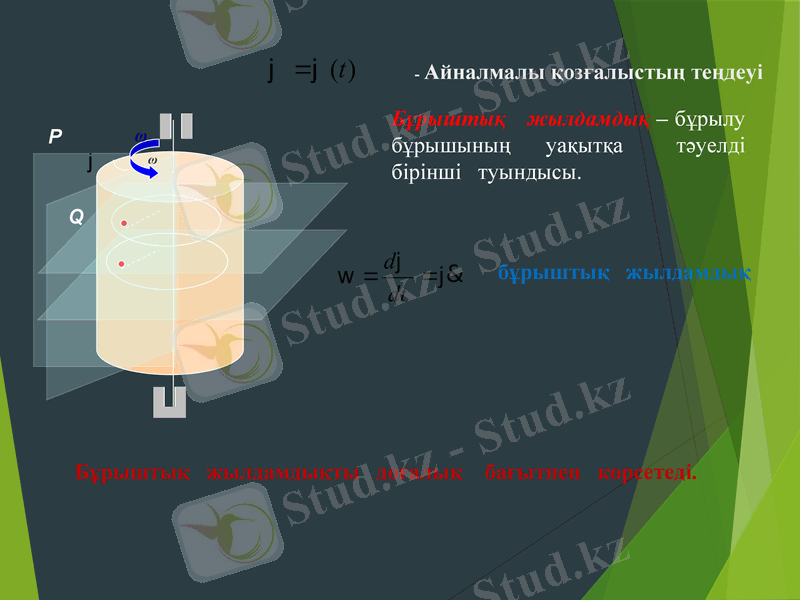
P
Q
ω
- Айналмалы қозғалыстың теңдеуі
Бұрыштық жылдамдық - бұрылу бұрышының уақытқа тәуелді бірінші туындысы.
бұрыштық жылдамдық
Бұрыштық жылдамдықты доғалық бағытпен көрсетеді.
ω
P
Q
ω
ε
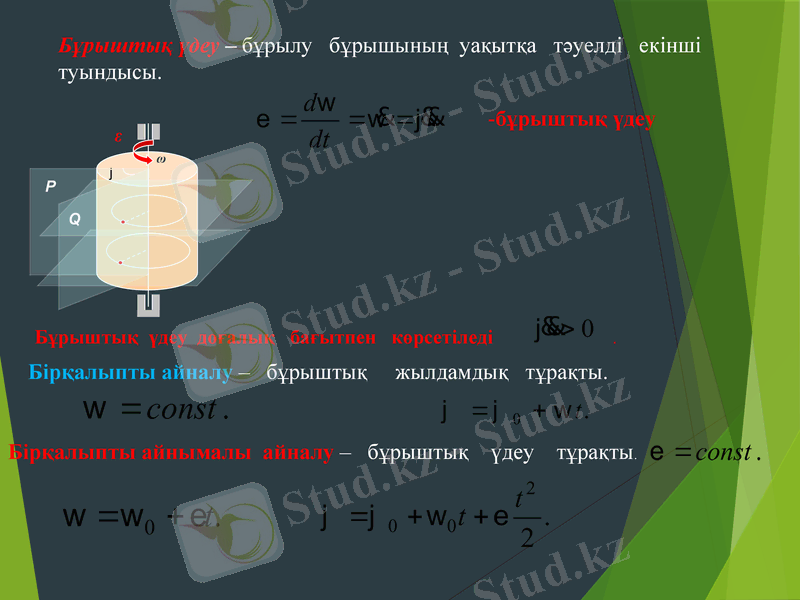
Бұрыштық үдеу - бұрылу бұрышының уақытқа тәуелді екінші туындысы.
бұрыштық үдеу
Бұрыштық үдеу доғалық бағытпен көрсетіледі .
Бірқалыпты айналу - бұрыштық жылдамдық тұрақты.
Бірқалыпты айнымалы айналу - бұрыштық үдеу тұрақты.

Айналмалы қозғалыстағы дене нүктесінің жылдамдығы -
R - дөңгелек радиусы, айналу өсі мен нүктенің арасындағы арақашықтық.
Доғаның ұзындығы:
Жылдамдық векторы, нүкте траекториясына жанаманың бойымен, айналудың бағытымен бағытталады.
Жылдамдық радиусқа тура пропорционал болады.
R
O
+
-
s
φ
ω

Айналмалы қозғалыстың үдеуі - нүктенің траекториясы белгілі болса, онда:
Жанама үдеу
айналмалы үдеу, радиусқа перпендикуляр, бұрыштық жылдамдықпен бағыттас
Тік нормаль үдеу
(центрге тартқыш)
Центрге тартқыш үдеу, радиустың бойымен айналу өсіне қарай бағытталады.
+
R
ε

Толық үдеу, ол екі вектордың қосындысына тең:
Толық үдеу мен радиустың арасындағы бұрыш радиусқа байланысты емес:
Айналмалы қозғалыстағы жылдамдық пен үдеудің векторы.
Бұрыштық жылдамдық пен бұрыштық үдеудің векторы айналу өсінің
бойымен доғалықтың бағыты сағат тіліне қарсы бағытталса жоғары
бағытталады.

Айналмалы қозғалыстағы жылдамдықтың векторы - бұрыштық жылдамдық пен радиус вектордың векторлық көбейтіндісіне тең:
1
2
Осы теңдеу - Эйлер теңдеуі деп аталады.

Айналмалы қозғалыстың жанама үдеу векторы - бұрыштық үдеу векторы мен радиус-векторының векторлық көбейтіндісіне тең,
Осы векторлық көбейтіндінің модулі:
Олай болса:
Үдеу векторының бағыты оң қол ережесі бойынша анықталады.

Айналмалы қозғалыстың центрден тепкіш( нормаль немесе тік) үдеуі - бұрыштық жылдамдық пен жылдамдық векторының векторлық көбейтіндісіне тең:
R
Бұл вектордың модулі:
Олай болса:
Векторлық көбейтіндіні былай жазуға болады:

Қатты дененің параллель жазық қозғалысы - дене нүктелері
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz