Графтар әдісі

Презентация қосу

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ
МИНИСТРЛІГІ
М.Әуезов атындағы Оңтүстік Қазақстан университеті

ЕТ ж\е БҚЕ кафедрасы

Презентация
Тақырыбы: Графтар саны: цикломатикалық,
хроматикалық, сыртқы және ішкі бірліктер.

Орындаған: Лесхан Ж.

Шымкент 2021 ж
Жоспар:
1 Эйлер теоремасы

2 Графтар әдісі

3 Цикломатикалық сан

4 Хроматикалық сандар

5 Ішкі тұрғындық жиыны

6 Сырттай тұрғын жиындар

37 Пайдаланылған әдебиеттер тізімі
Леонард Эйлер –
швейцариялық математик,
механик және физик. Базель
университетін бітірген. Графтің
әр бір қабырғасы бір рет кіретін
циклді эйлер циклі деп
аталады, ал осындай циклі бар
графті эйлер граф деп
аталады.Мұндай графтар түрін
анықтау проблемасы Л.
Эйлермен 1736 жылы
шешілді.Эйлер теоремасы. Бұл
ұғымдар 1736 жылы Эйлердің
Кенигсберг көпірлері туралы Леонард
жұмысында енгізілген. Эйлер
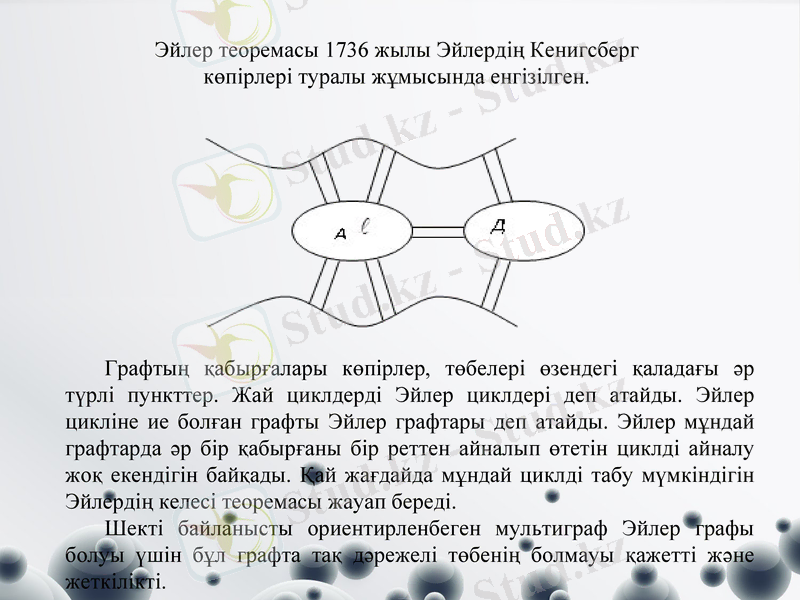
Эйлер теоремасы 1736 жылы Эйлердің Кенигсберг
көпірлері туралы жұмысында енгізілген.

Графтың қабырғалары көпірлер, төбелері өзендегі қаладағы әр
түрлі пункттер. Жай циклдерді Эйлер циклдері деп атайды. Эйлер
цикліне ие болған графты Эйлер графтары деп атайды. Эйлер мұндай
графтарда әр бір қабырғаны бір реттен айналып өтетін циклді айналу
жоқ екендігін байқады. Қай жағдайда мұндай циклді табу мүмкіндігін
Эйлердің келесі теоремасы жауап береді.
Шекті байланысты ориентирленбеген мультиграф Эйлер графы
болуы үшін бұл графта тақ дәрежелі төбенің болмауы қажетті және
жеткілікті.
Дәлелд
еу

Эйлер циклі
Қажеттілігі

Жеткіліктілігін
төбеден өтерде бір дәлелдеу үшін
қабырғадан кіріп графтың барлық

Жеткіліктілігі.
екінші қабырғадан төбелері жұп
шығуы керек. дәрежелі болсын
Сондықтан тақ деп ұйғарамыз.
дәрежелі төбенің
болмауы қажетті.
Егер шекті ориентирленбеген граф G(X) әр түрлі бас нүкте және
ақырғы нүкте -ге ие болса, онда ол Эйлер шынжыры деп аталады.
Графта Эйлер шынжыры бар болуы үшін оның байланысты және x(i)
және x(j) төбесінен басқа барлық төбелері жұп дәрежеге ие болуы
керек. x(i) және x(j) төбесі тақ дәрежелі болуы керек, себебі x(i)
төбеден бір рет артықша шығады, ал x(j) төбеге бір рет артықша
кіреді. Жоғарыдағы шарттар Эйлер шынжырының бар болуының
жеткілікті шарты.

x(i)

x(j)
Шекті байланысты ориентирленбеген G(X) графтың төбелері саны k-ға
тең болып, әрбір төбе тақ дәрежелі болса, онда G(X)-ты қаптайтын
қабырғалары бойынша қиылыспайтын шынжырлар саны k/2-ге тең.

Мұнда х1, х2, х3, х5 – тақ дәрежелі төбелер. (х2, х5) және (х1, х3)
қабырғаларды қосамыз. Онда келесі Эйлер циклдеріне ие болған
Эйлер графын аламыз: х , х , х , х , х , х , х , х , х . (х3, х1) қабырғаны алып
1 2 3 4 5 6 1 1 3

тастасақ Эйлер шынжырын аламыз. (х2, х5) қабырғаны алып тастасақ,
онда екі қаптаушы шынжырларды аламыз: х , х , х , х , х , х және х , х , х., х
1 2 3 4 5 2 5 6 1 3
Графтар әдісі
Графтар әдісімен техникадағы көп есептерді шешу графтардың
сипаттамасын анықтауға келтіріледі. Олардың 4 сипаттамасы бар.

Цикломатикалық Хроматикалық Ішкі Сырттай тұрғын
сан. G(X) графтың сандар.Р – натурал
n төбесі, т сан болсын. Егер тұрғындық жиындар.
қабырғасы және r G(X) графтың кез жиыны. G(X) – граф,Т Х .
байланысты келген екі төбесі әр
компонентасы түрлі бояумен А. Егер S X А. Егер Т-ға
болсын. боялған болса, жиынының кез тиісті болмаған
G m n r онда G(X) Р – келген екі кез келген төбені
хроматикалық граф
санды G графтың деп аталады. Граф
төбесі сыбайлас Т-ға тиісті болған
цикломатикалық Р – хроматикалық болмаса, яғни төбемен доға
саны деп атайды.
Бұл санның
болатын сандардың кез келген x S арқылы қосуға
ең кішісі G( x) S
физикалық төбе үшін болса, онда Т
хроматикалық сан
мағынасы зор. деп Ø болса, онда S жиынды сырттай
Электр Gаталады.
Оны
арқылы жиын G(X) тұрғын деп
шынжырларын белгілейміз. Егер
есептеудегі G 2 графтың іштей атайды.
байланыссыз болса, граф тұрғын жиыны
контурлар санын бихроматикалық
деп аталады. Демек, G( x) Т Ø.
анықтауда граф деп аталады.
қолданылады.
Пайдаланылған әдебиеттер тізімі

1. Соболева Т.С.. Дискретная математика : учебник для вузов. — М.:
Академия, 2014. - 256 с. ISBN 978-5-4468-0278-4.
2. Жетпісов Қ. Математикалық логика және дискретті математика,
Қарағанды, 2008.
3. Байсалов М.Ж. Дискрет математика. Оқу құралы. Алматы, 2007.
4. Тасқараев А., Оразов И. Математикалық логика және дискретті
математика. Оқу құралы. Шымкент, 2008.
5. Ахметова С.Т., Оспанова Р.Д. Дискретті математика. Оқу құралы.
2009.
6. Аляев Ю.А., Тюрин С.Ф. Дискретная математика. – М.: Финансы
и статистика, 2010. -385с.

Ұқсас жұмыстар

Графтың қасиеттері

Деректер қоры

Мектептегі дискретті математика элементтерін оқыту әдістемесі

Графтар теориясының элементтері

11-15 ғасырлардағы Италия, 7 - сынып

Графтың байланыс компоненттері

Ортағасырлық феодалдық қоғамның дамуы

Мәліметтер қорының басқа да модельдері

1-15ғғ. Франция, Германия, Италия

Бастауыш мектепте компьютерлік технологияны қолданудың қазіргі жағдайы

Пәндер