Бейсызықты автоматты басқару жүйелері

Презентация қосу

Қарағанды техникалық
университеті

В.Ф. Бырька атындағы кафедра

Автоматты басқару теориясы
пәніне дәрістік курс

6В07109 – Электр энергетикасы мамандық
студенттеріне арналған
ӨПА кафедрасының аға
оқытушысы:
Нурмағанбетова Ж.С.
Қарағанды техникалық
университеті
Дәріс 1, тақырыбы:
Бейсызықты автоматты
басқару жүйелері

1. Бейсызықты элементтердiң жiктелуі
және сипаттамалары.
2. Автоматты басқарудағы бейсызықты
жүйелердің ерекшеліктері
3. Бейсызықты сипаттамаларды
гармониялық сызықтандыру әдiсі
Бейсызықты элементтердiң
жiктелуі және сипаттамалары

Өздігінен жүретін сызықтық емес
тәуелділіктердің болуы бұл жүйенің күйін
сызықтық емес дифференциалдық теңдеулермен
сипаттауға әкеледі. Өздеріңіз білетіндей,
сызықтық емес теңдеулер топтарының көпшілігі
жалпы түрде шешілмейді және шешімдердің
нақты жағдайлары туралы ғана айтуға болады.
Сондықтан сызықтық емес жүйелерді зерттеуде
әртүрлі жуық әдістер үлкен рөл атқарады.
Сызықтық емес жүйелерді зерттеудің жуық
әдістері арқылы, әдетте, жүйенің барлық
динамикалық қасиеттері туралы толық түсінік алу
мүмкін емес, бірақ олардың көмегімен
тұрақтылық, өздігінен тербелістердің болуы, кез-
келген жеке режимдердің сипаты және т. б.
сияқты бірқатар маңызды сұрақтарға жауап
беруге болады.
Бейсызықты элементтердiң жiктелуі
және сипаттамалары

Автоматты басқарудың сызықты емес (бейсызық)
жүйесі – ең болмаса бір буыны сызықты емес
теңдеумен сипатталатын жүйе. Статикалық және
динамикалық сызықты емес жүйелер болып бөлінеді.
Бірінші сызықты емес алгебралық теңдеумен, екінші
сызықты емес дифференциалдық теңдеумен
сипатталады. Сызықты емес жүйенің жалпы
құрылымдық сұлбасын екі бөліктің қосылу түрінде
қарастырамыз: сызықты бөлігі – тұрақты
коэффициентті қарапайым сызықты
дифференциалдық теңдеулермен жазылатын жүйе
және бейсызық (сызықты емес) бөлігі – сызықты
емес элементтерден тұратын жүйе.
Бейсызықты элементтердiң жiктелуі және
сипаттамалары

Сызықты емес элемент инерциясыз, оның кіріс
шамалары және шығыс шамалары бір бірімен
алгебралық сызықты емес теңдеулермен
байланысты. Сызықты емес элементтердің
сипаттамасы әр түрлі болуы мүмкін. Сызықты
емес элементтерді екі түрге бөледі: жеткілікті
сызықты емес және жеткіліксіз сызықты емес.
Сызықты емес жеткіліксіз болып есептеледі,
егер оны сызықты элементпен
алмастырғанда жүйенің принципиалды
ерекшеліктері өзгермесе және сызықталған
жүйелердің процестері нақты жүйелердің
процестерінен айырмашылық болмаған
жағдайда. Егер алмастыру мүмкін емес және
сызықталған жүйелерде
айырмашылық үлкен болса, онда жеткілікті
сызықты емес болады.
Бейсызықты байланыстардың
негізгі сипаттамалары
Жеткілікті сызықты емес жүйелердің басты
ерекшелігі олар үшін суперпозиция принципі
орындалмайды, ал өтпелі процестердің
сипаттамасы
сыртқы әсер шамасынан және бастапқы
ауытқудан тәуелді болады. Қарапайым сызықты
емес элементтер болып статикалық сызықты емес
элементтер табылады. Оларда шығыс шамасы тек
кіріс шамасынан тәуелді,
яғни бұл тәуелділік бір мағыналы.
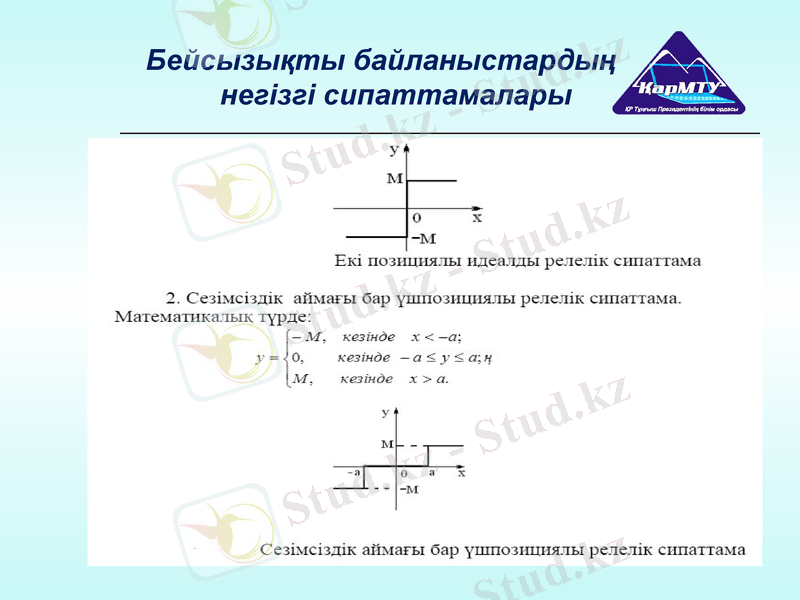
1. Идеалды релелік сипаттама.
Математикалық түрде:
Бейсызықты байланыстардың
негізгі сипаттамалары
Бейсызықты байланыстардың
негізгі сипаттамалары
Бейсызықты байланыстардың
негізгі сипаттамалары

4. Сезімсіздік аймағы бар және қанығусыз
релелік сипаттама.
Математикалық түрде:
Бейсызықты байланыстардың
негізгі сипаттамалары
Бейсызықты байланыстардың
негізгі сипаттамалары
Динамикалық сызықты емес жүйелерде шығыс
шамасы кіріс шамасынан және оның туындысынан
тәуелді. Динамикалық сызықты емес жүйелердің
сипаттамалары бір мағыналы емес. Суретте бір
мағыналы емес типтік сызықты емес сипаттамалар
келтірілген.
1. Гистерезисті релелік сипаттама.
Бейсызықты байланыстардың
негізгі сипаттамалары

Гистерезисті релелік
сипаттама
Бейсызықты байланыстардың
негізгі сипаттамалары

Сезімсіздік аймақ
тары
бар гистерезисті
релелік
сипаттама
Бейсызықты байланыстардың
негізгі сипаттамалары
Сызықты емес жүйелерді зерттеудің негізгі
есептері:
а) жүйенің тепе-теңдік күйін табу және
олардың орнықтылығын зерттеу;
б) автотербелісті анықтау және оларды
орнықтылығын талдау;
в) әр түрлі бастапқы ауытқулар кезінде
орныққан күйдегі өтпелі процестерді
зерттеу. Сызықты емес АБЖ зерттеу әдісі
екі негізгі топқа бөлінеді: нақты және
жуықтау әдістері. Нақты зерттеу әдісіне
фазалы жазықтық әдісі және Ляпунов әдісі
жатады.
Бейсызықты байланыстардың
негізгі сипаттамалары

Сызықтық емес жүйе – бейсызықты
дифференциалдық немесе алгебралық
теңдеулермен сипатталатын жүйе. Әдетте жүйе
сызықты емес байланыстың, яғни бейсызықты
дифференциалдық теңдеумен сипатталған
сілтеменің болуына байланысты алынады.
Бейсызықты байланыстарға мыналар жатады:
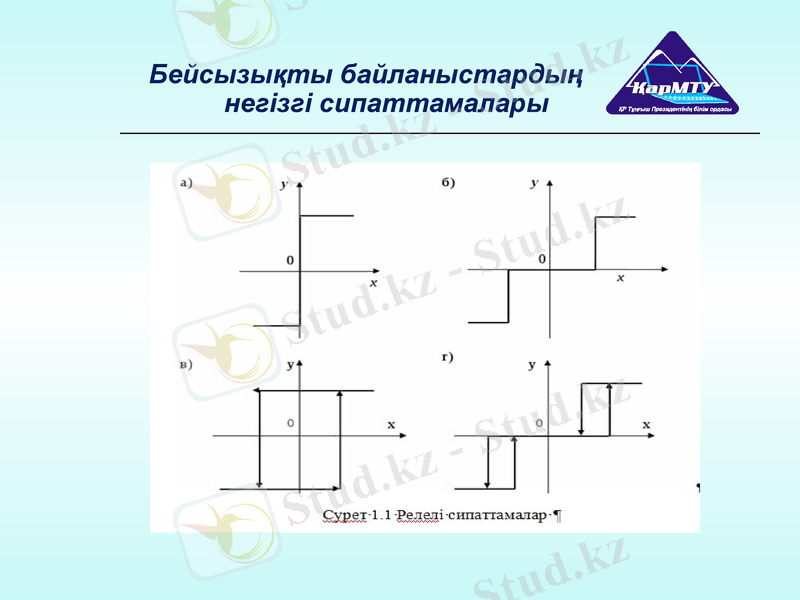
1) Релелік сипаттамасы бар буын (1.1 сурет);
2) Кесек-сызықтық типті сипаттамасы бар буын
(1.2-сурет);
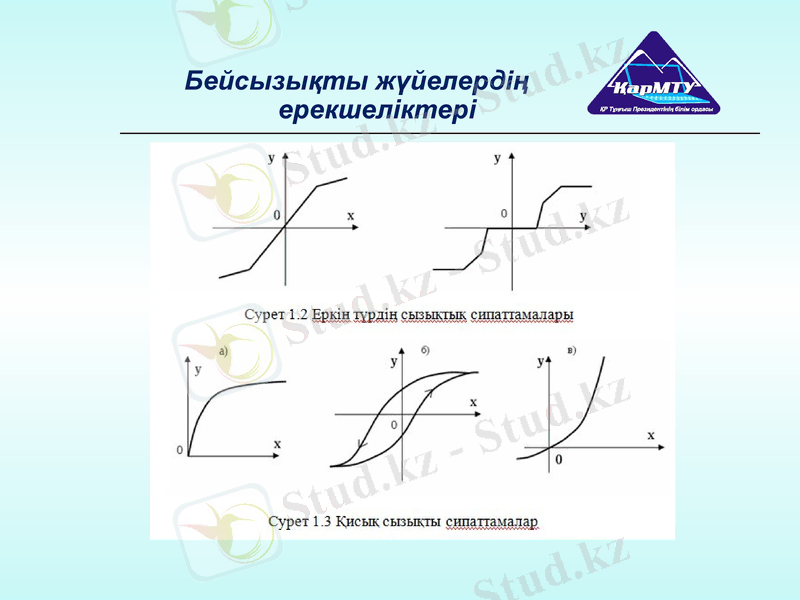
3) еркін түрдің қисық сызықты сипаттамасы бар
буын (1.3-сурет);
4) осы теңдеуге кіретін айнымалылардың немесе
олардың туындыларының көбейтінділерінің
есебінен сызықты емес болып табылатын буын;
5) жұмысы логикалық операцияларды
орындаумен байланысты буын.
Бейсызықты байланыстардың
негізгі сипаттамалары
Бейсызықты байланыстардың
негізгі сипаттамалары

Релелік сипаттамалары:
а) идеалды реле;
б) сезімталдық аймағы бар үш
позициялы реле;
в) гистерезисі бар екі позициялы
реле;
г) сезімталдық аймағы мен
гистерезисі бар үш позициялы реле.
Бейсызықты жүйелердің
ерекшеліктері
Бейсызықты жүйелердің
ерекшеліктері
Қисық сызықты сипаттамалар:
а) қанықтыру жүйелеріне тән сипаттама;
б) гистерезисі бар электромагниттік
құрылғылардың сипаттамасы;
в) түзеткіштің сипаттамасы.
Сызықтық емес статикалық сипаттамалардың
көптеген басқа түрлері бар.
Дифференциалдық теңдеудің сызықтық емес
болуына байланысты динамикада сызықтық
емес жағдайлар да бар. Сызықтық емес жүйені
сипаттайтын дифференциалдық теңдеулер
жиынтығында әдетте сызықтық байланыстарға
жататын бірнеше теңдеулер болады.
Бейсызықты тұйық АБЖ құрылымдық схемасы
төменде ұсынылған:
Бейсызықты жүйелердің
ерекшеліктері

Мұнда сызықтық бөлік кез-келген күрделіліктің
құрылымына ие болуы мүмкін (кері байланыс және
т.б.) және сызықтық дифференциалдық
теңдеулермен сипатталады. Сызықтық емес байланыс
сызықтық емес алгебралық немесе
дифференциалдық теңдеулермен сипатталады.
Бейсызықты жүйелердің
ерекшеліктері
Жүйенің ең дегенде бір элементінің сипаттамасы
елеулі бейсызықты болып келсе, онда бұл
жүйені бейсызықты деп атайды.
Мұндай жүйелердің
жұмысы бейсызықты дифференциал теңдеулер
арқылы өрнектеледі. Іс жүзінде инерциясыз
бейсызықты буыны бар жүйелер көп кездеседі.
Жүйедегі мұндай буынның болуы оның жалпы
динамикасының қасиеттеріне көп-көрім себебін
тигізеді. Мысалы: егер сызықты жүйе бастапқы
күйінен аз ауытқығанда орнықты болып қалса,
онда ол үлкен ауытқуда да орнықты болып
қалады, ал бейсызықты жүйе аз ауытқуда
орнықты болғанымен, үлкен ауытқуда орнықсыз
болуы мүмкін.
Бейсызықты жүйелердің
ерекшеліктері
Бұл тұрғыда мынандай жағдайларды
атап өткен жөн:
• біріншіден, бейсызықты АРЖ-ға
суперпозиция принципі
қолданылмайды;
• екіншіден, бейсызықты АРЖ өтпелі
процесінің сапасы жүйеге берілетін
қосымша қобалжыту әсерінің
көрсеткішіне тәуелді болады.
Бейсызықты жүйелердің
ерекшеліктері
Технологиялық процестің дұрыс өтуіне сәйкес
басқарылатын шаманың берілген уақыт аралығында
ұстап отыруға керекті мәнін алдын ала берілген мән
деп, ал фактілі, яғни процестің өлшенген мәнін
нақты (қазіргі) деп атайды. Реттелетін шаманың
алдын ала жоспарланған және нақты мәндерінің
арасындағы айырмасын ауытқу дейді. Осы қызмет
алгоритмін орындау үшін белгілі бір сыртқы
команданы орындайтын қоңдырғыны басқару
объектісі дейді.
Технологиялық процесті жүргізу үшін басқару
объектісіне әсер ететін тиімді ыкпалды басқару
дейді. Егер бұл басқару адамның қатысуынсыз жүзеге
асса, оны автоматты, ал адамның катысуымен
болса қолмен басқару деп атайды. Жалпы
технологиялық процестер орындалатын барлық
өндіріс жабдықтары басқару объектілеріне жатады.
Бейсызықты жүйелердің
ерекшеліктері

Жұмыс барысында автоматты басқару
жүйесіне әртүрлі ішкі және сыртқы әсерлер
ықпал жасайды. Автоматты жүйенің бір
бөлігінен келесі бөлігіне технологиялық
процестің бірқалыпты өтуін қамтамасыз
ететін әрекеттің тізбекті желісін құрайтын
әсерді ішкі әсер деп атайды. Оларды басқарушы
әсер дейді.
Ал сыртқы әсер екіге бөлінеді.
Технологиялық процестің тиянақты өтуіне
қажет әсер қызмет алгоритміне сәйкес жүйе
кірісіне беріледі де, жоспарланған әсер деп
аталады. Ал, жүйеге немесе басқару объектісіне
сыртқы ортадан берілетін әсерді қоздырғыш
әсер деп атайды.
Автоматты басқару жүйелерінің
жіктеуі
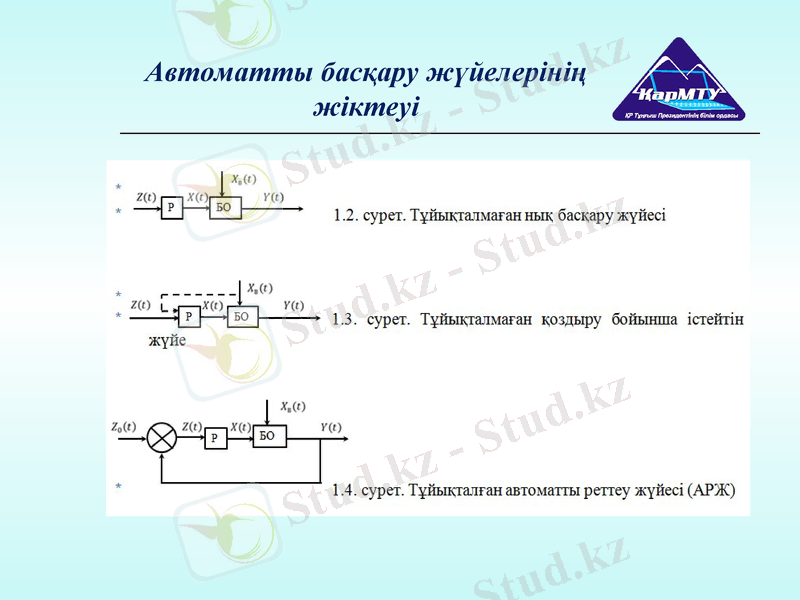
Автоматты басқару жүйелерінің
жіктеуі
Автоматты басқару жүйелерінің
жіктеу
Автоматты басқару жүйелерінің
жіктеу
Автоматты басқару теориясындағы пайдаланылатын
барлық мәселелерді екі үлкен класқа біріктіруге
болады ¾ автоматты жүйелерді талдау және
синтездеу мәселелері. Жүйені талдау деп толық
белгілі құрылымдық схемасы және берілген
параметрлері арқылы оның статикалық немесе
динамикалық қасиеттерін анықтауды айтады.
Жүйені жобалау және құрастыру кезеңіндегі
синтездің орны өте маңызды. Жалпы жағдайда
жүйені жобалау кезінде алгоритмдік және
функционалдық құрылымды анықтап алу қажет,
яғни синтездеудің мәселесін толық шешіп алу керек.
Жүйенің алгоритмдік құрылымын математикалық
модельдер және математикалық түрде анық
жазылған шарттар негізінде табады. Сондықтан
алгоритмдік құрылымды іздеу процедурасын
көбінесе теориялық синтез деп атайды.
Автоматты басқару жүйелерінің
жіктеу
Функционалдық құрылымның синтезі
немесе жүйенің техникалық синтезі
нақты элементтерді таңдаудан және
қосалқы элементтердің статикалық
және энергетикалық сипаттамаларын
өзара қиыстырудан тұрады.
Жобалаудың бұл сатысы инженерлік
тапқырлықты талап етеді. Жүйенің
синтезі деп автоматты реттеудің белгілі
сапа көрсеткіштері бойынша оның
құрылымдық схемасын, элементтері
арасындағы байланыстарды
анықтауды айтады.
Автоматты басқару жүйелерінің
жіктеу
Жалпы автоматты реттеу жүйесі, бір-
бірімен өзара байланысты реттелуші объект
пен реттеуші органнан тұратыны белгілі.
Бұл жүйені құрар алдында, сериялық
жабдықтар каталогынан реттеуші органды,
орындаушы құрылғыны, датчикті таңдап
алады. Бұл элементтер реттелуші
объектімен бірге жүйенің өзгермейтін
(берілген) бөлігін құрайды. Соңынан, жүйенің
статикалық және динамикалық
сипаттамаларына қойылатын талаптар
негізінде оның функционалдық және
корректирлеуші құрылғылардан тұратын,
өзгермелі бөлігін анықтайды.
Автоматты басқару
жүйелерінің жіктеу
Корректирлеуші құрылғылар жүйенің
контурына тізбектеле, параллель немесе кері
байланыс түрінде қосылып, оның динамикалық
қасиеттерін жоғарылатуға мүмкіндік
туғызады.
Сонымен, автоматты реттеу жүйесінің
синтезі келесі кезеңдерден тұрады:
1) Реттеу объектісінің қасиеттерін талдау,
статикалық және динамикалық
сипаттамаларын анықтау;
2) Реттеу жүйесін қанағаттандыратын реттеу
сапасының шарттарын, оптималдау
критерийлерін негіздеу және тұжырымдау;
3) Техникалық құралдарды таңдап алып, жүйенің
Автоматты басқару
жүйелерінің жіктеу
4) Оптимал динамикалық сипаттамаларды
синтездеу;
5) Оптимал режимді аппроксимациялау (жуықтату),
яғни, реттеу сапасымен жүйенің жұмысын іске
асырудың техникалық тұрғыдағы күрделі еместігі
және оның сенімділігі арасындағы ымыраға келе
отыра, жүйенің қалаулы динамикалық сипаттамасын
алу;
6) Бүкіл жүйенің қалаулы динамикалық сипаттамасын
толығымен қамтамасыз ететін, корректирлеуші
құрылғының динамикалық сипаттамасын анықтау;
7) Корректирлеуші құрылғының схемасын,
техникалық пайдалану жолын және параметрлерін
таңдап алу;
8) Қойылған талаптарға сай келетін, алынған
автоматты реттеу жүйесінің схемасына талдау
жүргізу.
Бақылау сұрақтары
1. Сызықтық емес жүйелердің тұрақтылығын
зерттеу әдістері әдетте қандай екі топқа
бөлінеді?
2. Бейнеленген нүкте ұғымына анықтама беріңіз.
3. Фазалық траектория ұғымын
анықтаңыз.Фазалық кеңістік ұғымына
анықтама беріңіз.
4. Қандай ерекше нүктелер мен арнайы
сызықтарды білесіз?
5. Қандай байланыстар сызықты емес?
6. Релелік сипаттамалардың қандай түрлерін
білесіз?
7. Сызықты емес жүйеге анықтама беріңіз.
8. Сызықты емес жүйелердің ерекшеліктері.
9. Жабық сызықты емес жүйенің жеңілдетілген
құрылымдық диаграммасын сызыңыз.
Студенттің өздік жұмысы
1. Типтік бейсызыкты үзбелердің математикалык
жазылуы.
2. Типтік бейсызыкты үзбелердің математикалык
жазылуы
3. Бейсызыкты жүйені коспалау әдісімен зерттеу
4. Бейсызыкты жүйені коспалау әдісімен зерттеу
5. Бейсызықты қадағалаушы жүйелер теңдеулері
6. Бейсызықты қадағалаушы жүйелер теңдеулері
7. Бейсызыкты жүйенің орныктылығын нүктелерді
түрлендіру әдісімен зерттеу.
8. Абсолюттік тұрақтылық критерийлары В.М. Попова
бойынша.
9. Сызық еместердің гармоникалық линиялдауы
10. Гармоникалық коэффициенттерді есептеу.
11. Стационарлық сызықсыз жүйелерді жобалап
зерттеу гармоникалық линиялдау әдісімен.
Студенттің өздік жұмысы
1. Бейсызыкты жүйенің орныктылығын нүктелерді
түрлендіру әдісімен зерттеу.
2. Ляпуновтын бірінші әдісімен орнықтылықты
анықтау.
3. Ляпуновтын бірінші әдісімен орнықтылықты
анықтау.
4. Сызықты емес жүйелердегі автотербелістердің
пайда болуы.
5. Сызықты емес жүйелердегі автотербелістер
орнықтылығын анықтау әдістері.
6. Сызықсыз жүйелердің тәлімдерінің
ерекшіліктері
7. Динамикалық сызық еместер.
8. Сызықсыз коррекция.
9. Сызықты емес АБЖ болатын өтпелі процестердің
сапасын бағалау
10. Дискреттік АБЖ типтерінің негізгі
сипаттамалары
Қолданылған әдебиеттер тізімі
1. Бекбаев А.Б., Сулеев Д.К., Хисаров Б.Д. Сызыкты жэне
бейсызыкты жуйелердщ автоматты реттеу теориясы.
Окулык. Алматы: Эверо, 2005. - 328 б.
2. Бекбаев А.Б., Сулеев Д.К., Хисаров Б.Д.Сызыкты жэне
бейсызыкты автоматты реттеу жуйесшц теориясы. Есептер
жинагы. Оку курал. Алма- ты: 2012.
3. В.А. Бесекерский, Е.П. Попов. Теория систем
автоматического управления. С-П., Профессия., 2003г. -
752с.
4. Воронов К.П. Теория автоматического управления.
Учебное пособие. Х., Изд-во Гуманитарный центр,2007, 526
с.
5. Ротач В.Я. Теория автоматического управления: учебник
для вузов. М.: Издательский дом МЭИ, 2007. - 400 с.
6. Гайдук А.Р., Беляев В.Е. Пьянченко Т.А. Теория
автоматического управления в примерах и задачах с
решением в MATLAB. Учебное пособие, СПБ: изд-во «Лань»,
2017.464 с.
Назарларыңызға рахмет!

Ұқсас жұмыстар

АВТОМАТТЫ РЕТТЕУ ЖӘНЕ ЖОСПАРЛЫ БАСҚАРУ

Автоматты реттеу және жоспарлы басқару жүйелерінің басқару құрылғылары

Функционалдық талаптар

Бағдарламаланатын логикалық контроллер

Бос радикалдар

Биологиялық басқару

Сұранысқа орай технология даму үстінде

Ғарыш аппараттарының жіктелуі

Автоматтандырылған ақпараттық

Зияткерлік ақпараттық жүйе

Пәндер