Филогенетикалық анализдің алгоритмдері

Презентация қосу

ЖОСПАР:

1.Филогенетикалық анализдің алгоритмдері.
2.Парсимония
3.Максимальды ықтималдылық әдісі
4.Байсовтық талдау
1. Өркен Айсулу, Медеуова Зере
2. Шараман Жанель, Қаржанбай
Азиза
3. Хажайхан Жанерке, Садикова
Эльвира
4. Сағындық Сәния, Қалқожа
Гүлмаржан
Филогенетикалық
анализдің
алгоритмдері.
Филогенетикалық анализ және
молекулалық эволюция
• Молекулалық деңгейде эволюция-бұл мутация және селекция процесі,
молекулалық эволюция өмір ағашының әртүрлі бұтақтарындағы гендер мен
ақуыздардың өзгеруін зерттейді. Филогенез-эволюциялық қатынастардың
көрінісі.
• Дәстүр бойынша филогения организмдер арасындағы морфологиялық
белгілерді салыстыруға негізделген. Қазіргі уақытта филогенетикалық
талдау үшін молекулалық тізбектер туралы мәліметтер де қолданылады.
Молекулалық эволюцияның міндеті:

Тірі жүйелердегі тұқым қуалайтын ақпараттың өзгеру
заңдылықтарын зерттеу, оның ішінде жасушалық емес және
жасушалық өмір формалары жер бетіндегі тіршіліктің даму
тарихын зерттеу ,тіршілік формалары (филогения)арасында
туыстық қатынастар орнату.
Филогенетикалық ағаштарды
құрудың негізгі алгоритмдері
• Қашықтықты бағалауға негізделген әдістер (матрицалық әдістер): барлық
жапырақтар (OTUs) арасындағы эволюциялық қашықтық есептеледі және
шыңдар арасындағы қашықтық жұптасқан қашықтық матрицасына сәйкес
келетін ағаш салынады.
• UPGMA
• Neighbor-joining
• Минималды эволюция
• Квартеттер ("топологиялық") ...
Филогенетикалық ағаштарды
құрудың негізгі алгоритмдері

Максималды үнемдеу (үнемділік),
Максималды ықтималдылық,
максималды парсимония, MP:
Maximum likelihood, mL: эволюция
Деректерді түсіндіруге қажетті
моделін қолданады және берілген
мутациялардың ең аз саны бар ағаш
модельде ең сенімді ағаш салынады
таңдалады.
• Гомология-жалпы ата-бабадан шыққан.
• Ұқсастық-қазір жинақталған деректер тарихи
гипотезаларды білдірмейді .
• Кластерлеу-белгілі бір белгілері бойынша ұқсас
объектілерді біріктіру (иерархиялық жіктеу).
• Филогения-биологиялық қатынастардың сипаттамасы,
әдетте филогенетикалық ағаш түрінде
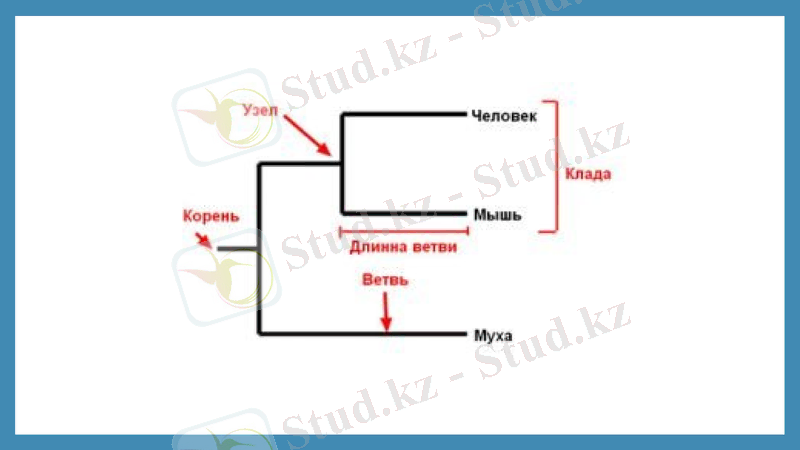
• Түйін (node) - ата-бабалар тізбегін (түр, популяция) тәуелсіз дамитын
екіге бөлу нүктесі. Эволюцияны бейнелейтін графиктің ішкі шыңына
сәйкес келеді.
• Жапырақ (leaf, OTU-жедел таксономиялық бірлік) - нақты (заманауи)
объект; графтың сыртқы шыңы.
• Филиал (филиал) — түйіндер арасындағы немесе түйін мен парақтың
арасындағы байланыс; графиктің шеті.
• Түбір (түбір) — гипотетикалық жалпы ата.
• Клада (clade) - екі немесе одан да көп таксалар тобы немесе ДНҚ тізбегі,
оның жалпы ата - бабасы да, оның барлық ұрпақтары да бар.
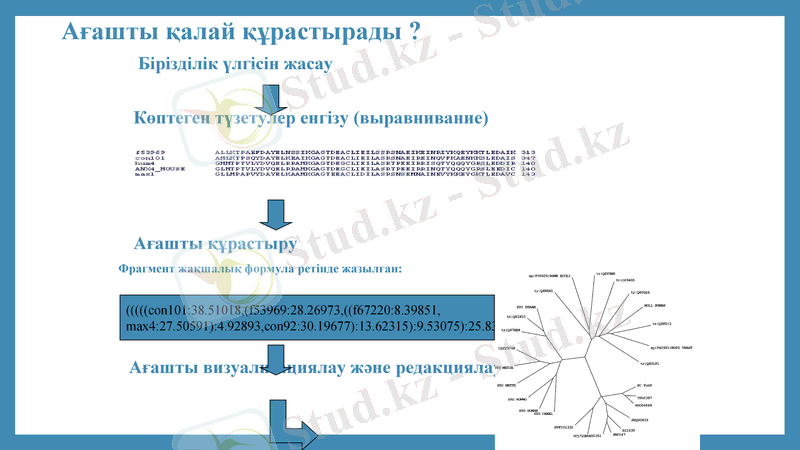
Ағашты қалай құрастырады ?

Бірізділік үлгісін жасау

Көптеген түзетулер енгізу (выравнивание)

Ағашты құрастыру
Фрагмент жақшалық формула ретінде жазылған:

(((((con101:38.51018,(f53969:28.26973,((f67220:8.39851,
max4:27.50591):4.92893,con92:30.19677):13.62315):9.53075):25.83145,

Ағашты визуализациялау және редакциялау
ПАРСИМОНИЯ
Қаржанбай Азиза, Шараман Жанель
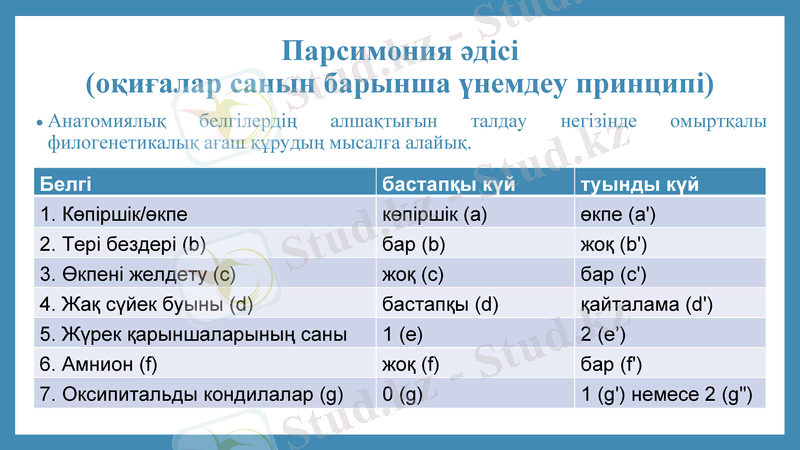
Парсимония әдісі
(оқиғалар санын барынша үнемдеу принципі)
•Анатомиялық белгілердің алшақтығын талдау негізінде омыртқалы
филогенетикалық ағаш құрудың мысалға алайық.

Белгі бастапқы күй туынды күй
1. Көпіршік/өкпе көпіршік (a) өкпе (a')
2. Тері бездері (b) бар (b) жоқ (b')
3. Өкпені желдету (c) жоқ (c) бар (c')
4. Жақ сүйек буыны (d) бастапқы (d) қайталама (d')
5. Жүрек қарыншаларының саны 1 (e) 2 (e’)
6. Амнион (f) жоқ (f) бар (f')
7. Оксипитальды кондилалар (g) 0 (g) 1 (g') немесе 2 (g")
Белгілердің таралуы
Туынды белгілері бойынша
ұқсастықтар қарастырылады.
Қызыл түспен белгіленген
белгілер шешуді қажет ететін
мәліметтер қақтығысын
тудырады.
Деректер қақтығыстары
нәтижесінде пайда болады:
параллелизм, риверсия,
кладаның негізін қалаушы
түрдің ішіндегі
полиморфизм. Ағаштың ең
үнемді нұсқаларын саламыз.
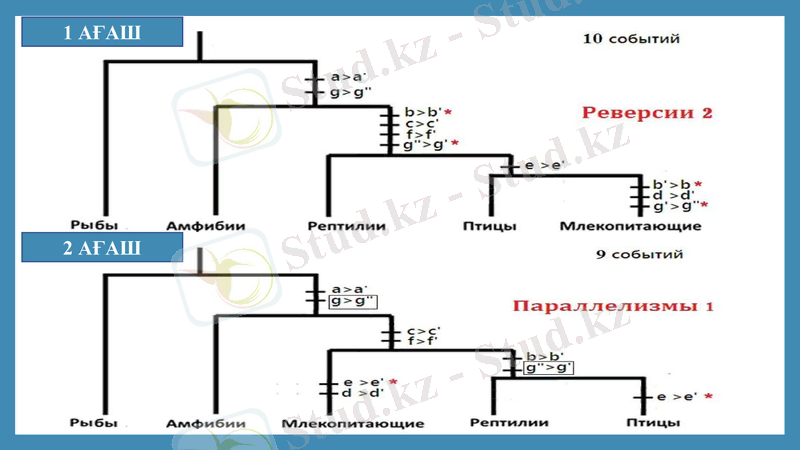
1 АҒАШ

2 АҒАШ
ПАРСИМОНИЯНЫҢ
ҚОЛДАНЫЛУЫ
• Талдауға өте көп ағаштар қосылған кезде, мүмкін ағаштардың саны күрт
артады.
•- 50 түрден тұратын топ үшін 3 x 10*76 мүмкін филогенетикалық ағаштар бар.
• Компьютерді қолдана отырып, ең жақсы ағашты табу үшін осындай деректер
көлемін талдау өте ұзақ уақытқа созылады.
• Систематиктер
парсимония (үнемділік) принципін көптеген мүмкін ағаштардың
ішінен талданған деректерді жақсы көрсететін бір ағашты таңдау үшін
қолданады.
• Филогенетикалық анализде парсимония ағашты таңдау үшін қолданылады, оны
алу үшін эволюциялық өзгерістердің ең аз саны қажет болды.
ПАРСИМОНИЯ ӘДІСІ
Ағаштардың барлық мүмкін топологияларын
талдайды

Белгінің эволюциялық жолы оның ең аз өзгеруін
қажет ететіндей болуы керек

Өзгерістердің ең аз саны бар ағашты таңдайды
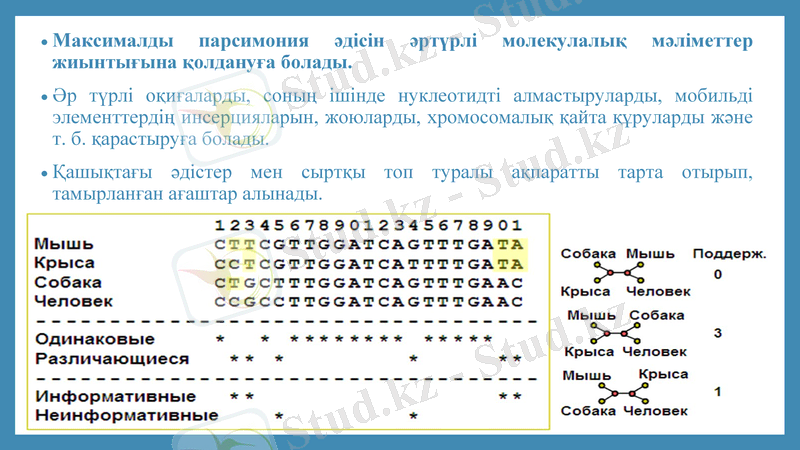
•Максималды парсимония әдісін әртүрлі молекулалық мәліметтер
жиынтығына қолдануға болады.
•Әр түрлі оқиғаларды, соның ішінде нуклеотидті алмастыруларды, мобильді
элементтердің инсерцияларын, жоюларды, хромосомалық қайта құруларды және
т. б. қарастыруға болады.
•Қашықтағы әдістер мен сыртқы топ туралы ақпаратты тарта отырып,
тамырланған ағаштар алынады.
Максималды ықтималдылық әдісі
Максималды ықтималдылық - филогенетикалық қатынастарды талдайтын ең
көп қолданылатын статистикалық әдістердің бірі. Бұл әдіс ықтималдық
моделіне негізделген филогенезді талдайды. Сонымен қатар, бұл әдіс орташа
мәнді де, дисперсияны да ескереді. Осылайша, филогенезде белгілі бір
организмнің берілген генетикалық деректеріне максималды ықтималдылық
алынады.
Максималды ықтималдылықтың статистикалық әдісін қолданудың
артықшылықтары мен кемшіліктері бар. Бұл әдіс генетикалық ақпаратты
қамтитын қарапайым мәліметтер жиынтығын талдау кезінде өте ыңайлы .
Генетикалық мәліметтер арасындағы дисперсия дәрежесі төмен болған кезде
ықтималдылықтың максималды баллдары сенімді болады. Максималды
ықтималдықпен алынған нәтижелер белгілі бір филогенетикалық қатынастың
парсимондық максималды балдарын растайды. Сондықтан ықтималдықтың
максималды талдауы растау тесті ретінде әрекет етеді.
Максималды ықтималдылық бен
парсимонияның ұқсастықтары
Максималды ықтималдылық бен максималды парсимония
- бұл филогенезде маңызды рөл атқаратын екі тәсіл.
● Екі әдіс те қолда бар генетикалық деректерге сүйене
отырып, организмнің өзінің ата -бабасына қатынасын
бейнелейді.
● Филогенетикалық ағаштарды максималды
ықтималдылық мен максималды парсимония арқылы
түсіндіруге болады.
● Екі техникада да генетикалық деректер ДНҚ немесе
РНҚ реттілігіне сүйенеді.
● Екі әдіс те филогенетикалық ағаштарды өсіруде
маңызды.
Максималды ықтималдылық беен максималды парсимонияның
айырмашылығы неде?
Максималды ықтималдылық мен максималды парсимония - бұл филогенетикалық
ағашты түсіндіруде екі түрлі тәсіл. Максималды парсимония бірнеше ерекшеліктерді
талдауға және ағзадан организмге сипаттың өзгеруін азайтуға әсер етеді. Керісінше,
ықтималдықтың максималды әдісі орташа мәнді де, дисперсияны да ескереді және
белгілі бір организмнің берілген генетикалық деректерінің максималды ықтималдығын
алады.

Сонымен қатар, максималды парсимонияның сенімділігі ғана қорытынды жасауға
жеткіліксіз. Бірақ, ықтималдылықтың максималды әдісі максималды парсимонияның
нәтижелерін растайтын тест ретінде әрекет етеді. Осылайша, қорытынды ең жоғары
ықтималдылықпен де, максималдылықпен де жасалуы керек.
Төмендегі инфографика максималды парсимония мен максималды ықтималдылық
арасындағы айырмашылықты көрсетеді.
Максималды ықтималдылық мен максималды парсимония
Филогенез филогенетикалық ағаштарды құру арқылы
эволюциялық қатынастарды анықтауда маңызды рөл
атқарады. Максималды парсимония - бұл таңба күйінің
өзгеруінің ең аз саны бар ағаш салу әдісі. Керісінше,
филогенетикалық ағаштың максималды ықтималдығы
генетикалық деректер арасындағы максималды ұқсастықты
қолдануға негізделген. Екі талдау үшін де деректер ДНҚ
немесе РНҚ тізбектік деректерінен алынады. Ағаш құрылысы
екі техниканың көмегімен жүзеге асқанда сенімділік пен дәлдік
жоғары болады. Осылайша, бұл максималды парсимония мен
максималды ықтималдылық арасындағы айырмашылықты
қорытындылайды.
Байсовтық талдау
•Жиі келу статистикасы
•Жиі келу статистикасындағы туа біткен кемшіліктер
•Байес статистикасы
•Шартты Ықтималдық
•Байес Теоремасы
• Байсовтық талдау-бұл ықтималды мәлімдемелерді қолдана отырып, белгісіз параметрлер туралы
зерттеу сұрақтарына жауап беретін статистикалық парадигма.
• Мысалы, ер адамның орташа биіктігі 70-тен 80 дюймге дейін немесе әйелдің орташа биіктігі
60-тан 70 дюймге дейін болуы ықтималдығы қандай? Белгілі бір штаттағы адамдар
республикашыларға немесе демократтарға дауыс беру ықтималдығы қандай? Қылмыс жасады
деп айыпталған адамның кінәлі болу ықтималдығы қандай? А емінің нақты медициналық
провайдер үшін В емінен гөрі үнемді болу ықтималдығы қандай? Егер А препараты
тағайындалса, науқастың қан қысымының төмендеуі ықтималдығы қандай? Және тағы басқалар.
• Мұндай ықтималды тұжырымдар Байес талдауы үшін табиғи болып табылады, өйткені барлық
параметрлер кездейсоқ шамалар болып табылады. Байес анализінде параметр классикалық
жиілік анализіндегідей бір тұрақты мәннің орнына мәндердің барлық таралуы бойынша
жинақталады. Бұл үлестіруді бағалау, қызығушылық параметрінің кейінгі таралуы Байес
талдауының негізінде жатыр.
Постериори үлестірімі алдын-ала параметрді бөлуді және бақыланатын мәліметтер
негізінде параметр туралы ақпарат беретін сенімділік моделін қамтиды. Таңдалған
алдын-ала үлестіру моделіне және сенімділікке байланысты, артқы үлестіру
аналитикалық түрде қол жетімді немесе жақын, мысалы, Марков тізбегінің Монте-
Карло әдістерінің бірі (MCMC).

Байес тұжырымы модель параметрлері үшін әр түрлі жиынтықтарды
қалыптастыру үшін артқы үлестірімді қолданады, оның ішінде артқы орташа
мәндер, медианалар, процентильдер және сенімді интервалдар деп аталатын
аралық бағалаулар. Сонымен қатар, модель параметрлерінің барлық статистикалық
тестілері бағаланған кейінгі үлестірімге негізделген ықтималды мәлімдемелер
түрінде көрсетілуі мүмкін.

Байес талдауының ерекше белгілері талдауға алдын-ала ақпаратты қосу, сенімді
аралықтарды алдын-ала анықталған ықтималдығы бар параметр белгілі болатын
белгіленген диапазон ретінде интуитивті түсіндіру және кез-келген қызығушылық
гипотезасына нақты ықтималдылықты тағайындау мүмкіндігін қамтиды.
Жиі келу статистикасы
Жиілік статистикасы оқиғаның (гипотезаның) бар-жоғын тексереді. Ол
эксперименттің ұзақ мерзімді перспективасындағы оқиғаның ықтималдығын
есептейді (яғни нәтиже алу үшін эксперимент бірдей жағдайларда
қайталанады).Мұнда белгіленген мөлшердің таңдаулы үлестірімдері алынады. Содан
кейін эксперимент теориялық тұрғыдан шексіз рет қайталанады, бірақ іс жүзінде
тоқтату ниетімен орындалады. Мысалы, мен экспериментті 1000 рет қайталанған
кезде тоқтататынымды немесе монетаны лақтырған кезде кем дегенде 300 Гол
көретінімді ескере отырып, оны тоқтату ниетімен өткіземін.
Жиі келу статистикасындағы туа біткен кемшіліктерОсы уақытқа дейін біз жиі
келу статистикасының бір ғана кемшілігін көрдік.20 ғасырда сандық модельдерге
қолданылатын жиілік статистикасының жаппай өсуі болды, бір үлгінің екіншісінен
ерекшеленетінін тексеру үшін, параметр оны модельде сақтауға жеткілікті
маңызды және гипотезаларды тексерудің басқа да көріністері. Бірақ жиі келу
статистикасы олардың дизайны мен түсіндірілуінде елеулі кемшіліктерге ие
болды, бұл өмірдің барлық нақты мәселелеріне үлкен алаңдаушылық тудырды.
Мысалы:
1. p-белгілі бір тоқтату ниеті бар іріктеу статистикасы (белгіленген өлшем)
бойынша өлшенген мәндер үлгінің ниеті мен мөлшерінің өзгеруімен өзгереді.
яғни, егер екі адам бірдей деректермен жұмыс істесе және әртүрлі тоқтату
ниеті болса, олар бірдей деректер үшін екі түрлі p мәндерін ала алады, бұл
қажет емес.Мысалы: А адамы монетаны лақтыруды жалпы саны 100-ге
жеткенде тоқтата алады, ал Б 1000-ға тоқтайды. Үлгінің әртүрлі өлшемдері
үшін біз әртүрлі t-баллдар мен әртүрлі p-мәндерді аламыз. Сол сияқты, тоқтату
ниеті төңкерістердің белгіленген санынан төңкерістің жалпы ұзақтығына
өзгеруі мүмкін. Бұл жағдайда біз әр түрлі p мәндерін аламыз.
2-сенімділік аралығы (C. I), p мәні сияқты, үлгінің мөлшеріне байланысты. Бұл
тоқтау потенциалын мүлдем абсурд етеді, өйткені қанша адам бірдей деректерге
сынақ жүргізсе де, нәтижелер дәйекті болуы керек.
3-сенімділік интервалдары (C. I) ықтималдылықты бөлу емес, сондықтан олар
параметрдің ең ықтимал мәнін және ең ықтимал мәндерді қамтамасыз етпейді.
Байес статистикасы"Байес статистикасы-статистикалық есептерге
ықтималдылықты қолданатын математикалық процедура. Бұл адамдарға
жаңа деректерді дәлелдеуде сенімдерін жаңарту құралдарын
ұсынады".Ники лауда мен Джеймс Хант арасындағы барлық 4
чемпионаттың (F1) ішінен Ники 3 рет жеңді делік, ал Джеймс тек 1
жеңді.Сонымен, егер сіз келесі жарыстың жеңімпазына ставка жасасаңыз,
ол кім болар еді?Сіз Ники Лаудты айтар едіңіз.Міне, қиындық. Егер сізге
Джеймс жеңіске жеткенде және Никки жеңген кезде бір рет жаңбыр жауды
деп айтылса, не істеу керек, және келесі күні жаңбыр жауады. Сонымен,
сіз қазір ақшаңызды кімге қоясыз? Интуитивті түрде Джеймстің жеңіске
жету мүмкіндігі күрт артқанын байқауға болады. Бірақ сұрақ: Қанша?
Қарастырылып отырған мәселені түсіну үшін біз кейбір ұғымдармен
танысуымыз керек, олардың біріншісі-шартты ықтималдық.
Шартты ықтималдық.
Ол келесідей анықталады:B-ге берілген А оқиғасының ықтималдығы B және A
ықтималдығына бөлінген бірге болу ықтималдығына тең."Мысалы: төменде
көрсетілгендей екі жартылай қиылысатын А және В жиынтығы делік.А жиынтығы
оқиғалардың бір жиынтығын, ал В жиынтығы екіншісін білдіреді. Біз берілген B-
нің болу ықтималдығын есептегіміз келеді. В оқиғасын қызыл түспен бояйық.
Байсовтық талдау.

Филогенияның байесиялық тұжырымы алдыңғы және ықтималдық
моделіндегі мәліметтерді ескере отырып, ағаштың дұрыс болу
ықтималдығын білдіретін ағаштардың кейінгі ықтималдығын құру
үшін алдыңғы және мәліметтер ықтималдығындағы ақпаратты
біріктіреді. 1990 жылдары молекулалық филогенетикаға үш тәуелсіз
топ енгізілді: Берклидегі Брюс Раннала және Цихенг Янг,
Мэдисондағы Боб Мау және Айова университетіндегі Шуин Ли, сол
кездегі соңғы екеуі аспиранттар болды. Бұл тәсіл 2001 жылы
MRBayes бағдарламалық жасақтамасы шыққаннан бері өте танымал
болды және қазіргі уақытта молекулалық филогенетикадағы ең
танымал әдістердің бірі болып табылады.
Филогенетикалық қайта құруға байесиялық көзқарас P(A) ағашының априорлық
ықтималдығын P (A|B) ағаштарындағы ықтималдылықтың кейінгі таралуын алу
үшін мәліметтер ықтималдығымен(B) біріктіреді. Aғаштың кейінгі ықтималдығы-
бұл алдыңғы мәліметтер мен сенімділік моделінің дұрыстығын ескере отырып,
ағаштың дұрыс болу мүмкіндігі.MCMC әдістерін үш кезеңмен сипаттауға болады:
-Aлдымен стохастикалық механизммен Марков тізбегі үшін жаңа күй ұсынылады.
-Екіншіден, бұл жаңа мемлекеттің дұрыс болуы ықтималдығы есептеледі. -
Үшіншіден, жаңа кездейсоқ мән ұсынылады (0,1).
Егер бұл жаңа мән қабылдау ықтималдығынан аз болса,жаңа күй қабылданады
және тізбек күйі жаңартылады. Бұл процесс мыңдаған немесе миллиондаған рет
орындалады. Тізбектегі бір ағашқа бару саны оның кейінгі ықтималдығына
жақындау болып табылады. MCMC әдістерінде қолданылатын кейбір кең таралған
алгоритмдерге Метрополис–Хастингс алгоритмдері, метрополисі бар MCMC
(MC3) және Ларгет пен Саймонның жергілікті алгоритмі кіреді.
Метрополис–Хастингс Алгоритмі
MCMC–тің ең көп қолданылатын әдістерінің бірі-Метрополис-Хастингс алгоритмі,
бастапқы Метрополис алгоритмінің өзгертілген нұсқасы. Бұл күрделі және көп
өлшемді таралу ықтималдығынан кездейсоқ іріктеудің кеңінен қолданылатын
әдісі. Metropolis алгоритмі келесі қадамдарда сипатталған:Бастапқы ағаш, Ti,
кездейсоқ таңдалады.Көршілес ағаш, Tj, ағаштар жиынтығынан таңдалады.R,
ықтималдық (немесе ықтималдық тығыздығының функциялары) қатынасы Tj және
Ti келесідей есептеледі: R = f (Tj) / f (Ti)Егер R ≥ 1 болса, Tj ағымдағы ағаш
ретінде қабылданады.Егер R <1 болса, Tj R ықтималдығы бар ағымдағы ағаш
ретінде қабылданады, әйтпесе Ti сақталады.Бұл кезеңде процесс 2-қадамнан N рет
қайталанады.Алгоритм тепе-теңдік үлестіріміне жеткенше жұмысын
жалғастырады. Сондай-ақ, біз Ti ағашының ескі күйінде болған кезде жаңа Tj
ағашын ұсыну ықтималдығы TJ-де болған кездегі ti сөйлемінің ықтималдығына
тең болады деп болжайды. Олай болмаған кезде Хастингс түзетулері қолданылады.
Метрополис-Хастингс алгоритмінің мақсаты-Марков процесі стационарлық
үлестірімге жеткенше белгілі бір үлестірімі бар күйлер жиынтығын құру.
Алгоритм екі компоненттен тұрады:Qi,j ауысу ықтималдығы функциясын қолдана
отырып, бір күйден екінші күйге (i → j) өту мүмкіндігіТізбектің J күйіне ai,j
ықтималдығымен қозғалысы және i – де 1-ai,j ықтималдығымен қалады.
Қолдану саласы:
Байес теориялары мен желілері интуитивті түсінікке және тиісті
бағдарламалық жасақтаманың болуына байланысты кеңінен
қолданылады. Байес желілері әртүрлі салаларда қолданылады:
медициналық диагностика, суретті модельдеу, генетика, сөйлеуді тану,
экономика, ғарышты зерттеу және қазіргі іздеу жүйелері. Олар
құрылымдық байланыстар мен деректерді пайдалану арқылы белгісіз
айнымалыларды құру қажет болатын кез-келген салада қосымшаны таба
алады. Байес желілерін себептік байланыстарды зерттеу, проблемалық
аймақты түсінуді тереңдету және жүйеге араласудың салдарын болжау
үшін қолдануға болады.
Артықшылықтары мен кемшіліктері
Артықшылықтары:
Кемшіліктері:

-Күрделі жүйелер үшін Байес
-Әдісті қолдану үшін
желілеріндегі барлық өзара
априорлық ақпаратты білу
әрекеттесулерді анықтау
жеткілікті.
әрдайым мүмкін емес.
-Логикалық тұжырымдалған
-Байес тәсілі әдетте
тұжырымдарды түсіну оңай.
сараптамалық әдістермен
-Әдісті қолдану Байес
алынған көптеген шартты
формуласына негізделген.
ықтималдықтар туралы
-Бұл әдіс субъективті
білімді қажет етеді.
ықтималды бағалауды қолдану
-Бағдарламалық жасақтаманы
әдісі болып табылады.
қолдану сараптамалық
бағалауға негізделген.
MRBAYES бағдарламалық
жасақтамасы
• MrBayes-бұл филогенияның байесиялық тұжырымын орындайтын ақысыз
бағдарламалық құрал. Алғашқыда Джон П. Уэльсенбек пен Фредерик
Ронквист 2001 жылы жазған. Байес әдістерінің танымалдығы өскен сайын,
MrBayes көптеген молекулалық филогенетиканы таңдаған бағдарламалардың
біріне айналды. Ол Macintosh, Windows және UNIX операциялық жүйелеріне
ұсынылады және командалық жол интерфейсіне ие. Бағдарламада стандартты
MCMC алгоритмі, сондай-ақ Metropolis-пен байланысты MCMC нұсқасы
қолданылады. MrBayes стандартты NEXUS форматында тураланған тізбекті
матрицаларды (ДНҚ немесе амин қышқылдары) оқиды
• MrBayes ағаштардың кейінгі ықтималдығын жуықтау үшін
MCMC қолданады. Пайдаланушы ауыстыру моделінің
болжамдарын, алдын-ала деректерді және MC талдау
мәліметтерін өзгерте алады. Сондай-ақ, бұл пайдаланушыға
талдауға таксалар мен таңбаларды жоюға және қосуға мүмкіндік
береді. Бағдарламада ДНҚ-ны алмастырудың ең стандартты
моделі, 4x4, сонымен қатар JC69 деп аталады, ол нуклеотидтер
арасындағы өзгерістер бірдей ықтималдылықпен жүреді деп
болжайды.[30] ол сонымен қатар 20x20 аминқышқылдарын
алмастырудың бірқатар модельдерін және ДНҚ алмастырудың
кодондық модельдерін жүзеге асырады. Ол нуклеотидті сайттар
арасындағы тең алмастыру жылдамдығы туралы болжамды
жеңілдетудің әртүрлі әдістерін ұсынады. MrBayes сонымен қатар
филогенетикалық ағаш пен модель параметрлерінің белгісіздігін
ескеретін ата-бабалардың күйлерін шығара алады.
• MrBayes 3 түпнұсқа MrBayes-тің толық қайта құрылған және
қайта құрылымдалған нұсқасы болды. Бағдарламалық
жасақтаманың деректер жиынтығының гетерогенділігін ескеру
қабілеті басты жаңалық болды. Бұл жаңа құрылым қолданушыға
модельдерді араластыруға және әртүрлі мәліметтер түрлерімен
(мысалы, ақуыз, нуклеотид және морфологиялық) жұмыс жасау
кезінде MCMC Байес талдауының тиімділігін пайдалануға
мүмкіндік береді. Әдепкі бойынша, ол мегаполисті
байланыстыратын MCMC қолданады.
• MrBayes 3.2 2012 жылы шығарылды.Жаңа нұсқа
пайдаланушыларға параллель бірнеше талдау жасауға мүмкіндік
береді. Сондай-ақ, ол ықтималдылықтың жылдам есептеулерін
қамтамасыз етеді және бұл есептеулерді графикалық өңдеу
бірлестіктеріне (GPU) беруге мүмкіндік береді.

Ұқсас жұмыстар

Филогенетикалық систематика, финетика

Систематикадағы гомология

Тірі организмді классификациялау ерекшеліктері

Филогенетика казіргі кезеңі

Көпфакторлы дисперсиялық талдау

Систематиканың негіздері

Электродты потенциал

ГРАВИМЕТРИЯЛЫҚ АНАЛИЗ.ГРАВИМЕТРИЯЛЫҚ АНАЛИЗДІ ЖОСПАРЛАУ,ҰЙЫМДАСТЫРУ. КРИСТАЛДЫҚ,АМОРФТЫ ТҰНБАЛАРДЫ ТҰНДЫРУ

Фармакоэкономикалық анализ

Физикалык - химиялық талдау әдістері

Пәндер