Стереометрия: кеңістіктегі фигуралар, көпжақтар, айналу денелері және есептер



Тақырыбы: Кеңістіктегі фигуралар. Стереометрияның стандарт емес есептері
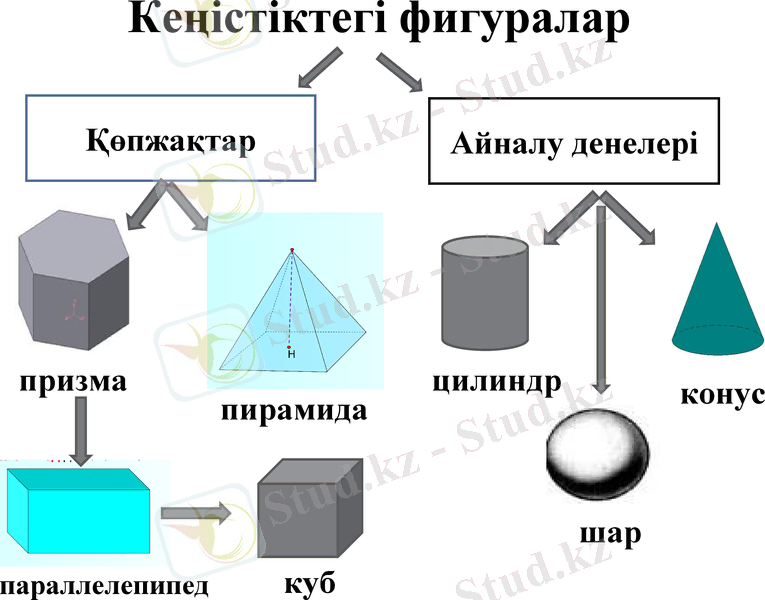
Кеңістіктегі фигуралар
Қөпжақтар
Айналу денелері
призма
параллелепипед
куб
пирамида
цилиндр
конус
шар

Қоршаған ортада

Платон (көне грекше: Πλάτων, б. з. д. 427 - 347) - ежелгі грек философы, математик, Сократтың шәкірті, еуропалық идеализм
философиясының негізін салушы. Платон оның лақап аты болып, жауырыны кең болғандықтан "жалпақ", "кең" деген мағынада Платон деп аталған. Платонның шын есімі - Аристокль.




Егер, дөңес көпжақтың жақтары қабырғаларының саны бірдей дұрыс көпжақтар және көпжақтың әрбір төбесінен шығатын қырларының саны бірдей болса, онда оны дұрыс көпжақ деп атайды.
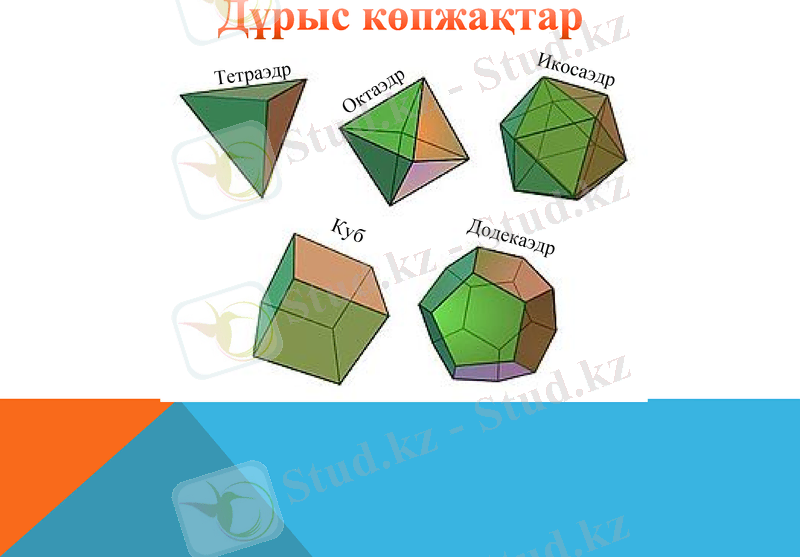
Дұрыс көпжақтар
Тетраэдр
Октаэдр
Куб
Додекаэдр
Икосаэдр
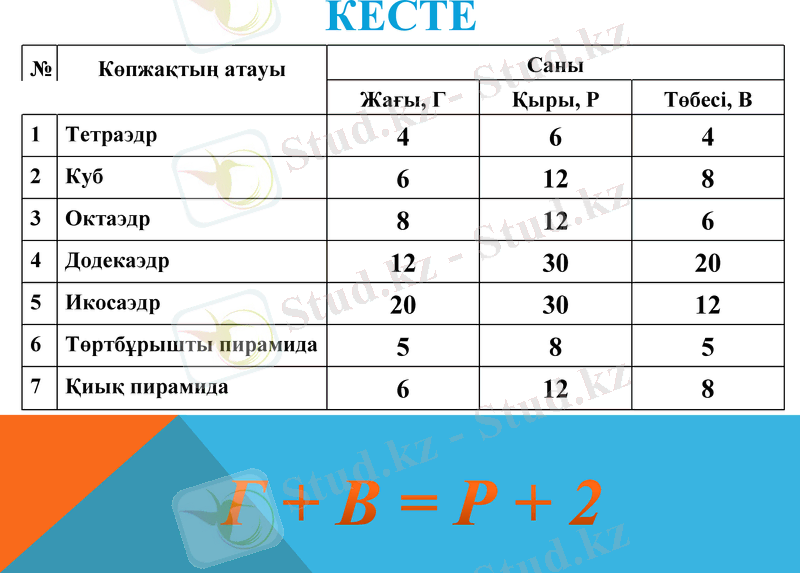
КЕСТЕ
№
Көпжақтың атауы
Саны
Жағы, Г
Қыры, Р
Төбесі, В
1
Тетраэдр
4
6
4
2
Куб
6
12
8
3
Октаэдр
8
12
6
4
Додекаэдр
12
30
20
5
Икосаэдр
20
30
12
6
Төртбұрышты пирамида
5
8
5
7
Қиық пирамида
6
12
8
Г + В = Р + 2

Эйлер теоремасы
Дөңес көпжақтың жақтарының санын Г, қырларының санын Р, төбелерінің санын В деп белгілесек, онда Г + В = Р + 2 болады.
Леонард Эйлер
(1707 - 1783 ж. ж. )

Платон денелері
Тетраэдр
ОТ
Додекаэдр
КҮН
Куб
ЖЕР
Октаэдр
АУА
Икосаэдр
СУ

Формулалар

Есептер шығару:
№2
Тікбұрышты параллелепипедтің табан қабырғалары 7дм, 24дм. Ал биіктігі 8дм. Диагональдық қиманың ауданын тап.

Жауабы:
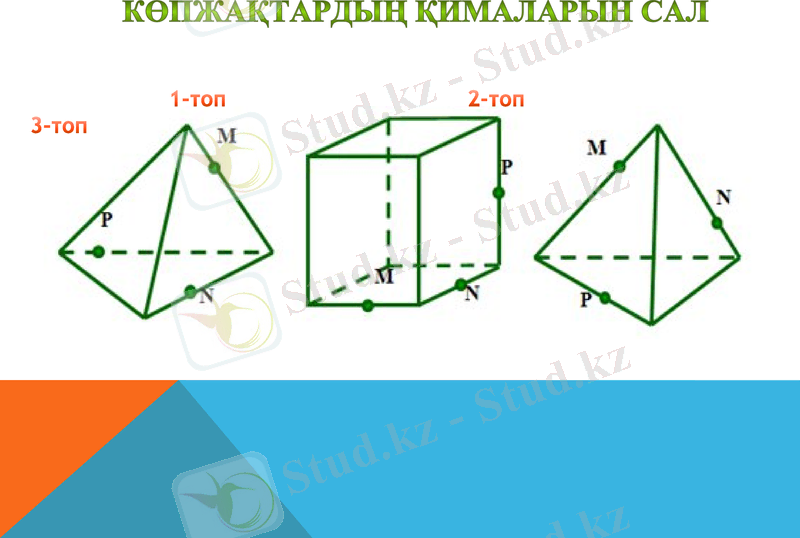
Көпжақтардың қималарын сал
1-топ 2-топ 3-топ
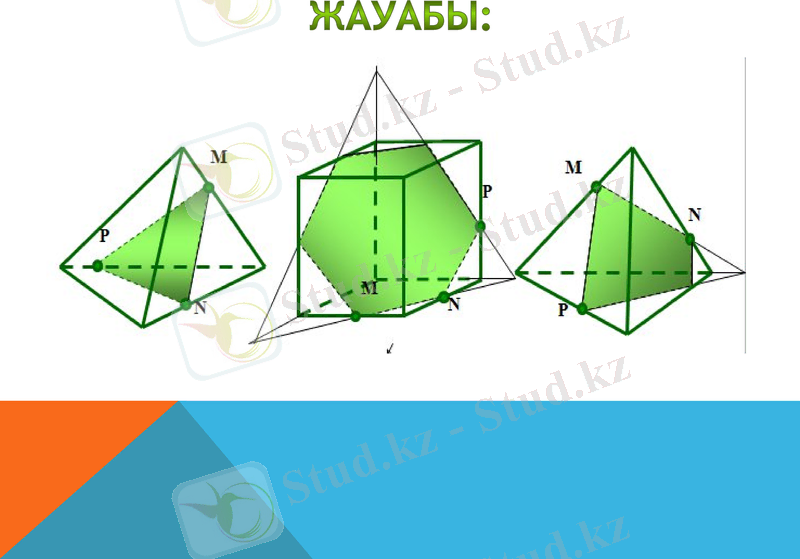
ЖАУАБЫ:

Есеп 1

Есеп 2

Есеп 3
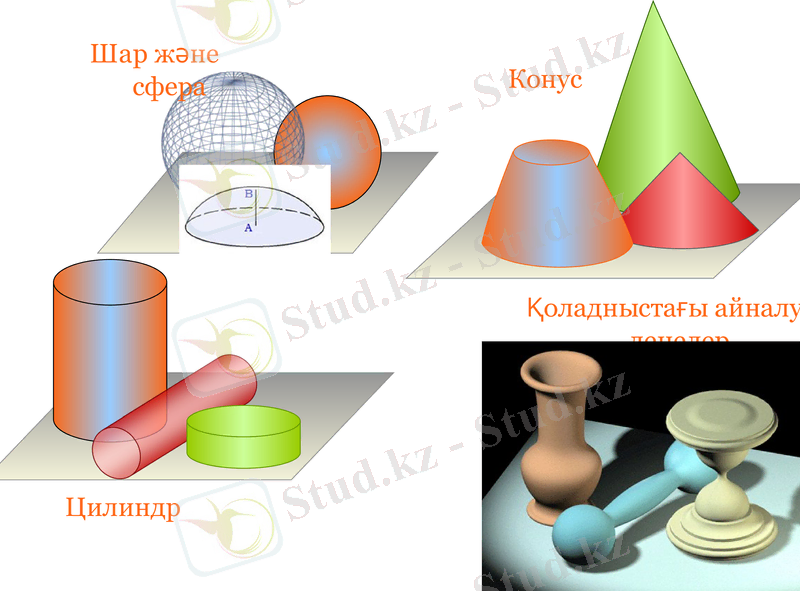
Цилиндр
Конус
Шар және сфера
Қоладныстағы айналу денелер

Айналу денесі - кеңістіктегі геометриялық фигура. Ол жазықтықтағы шектелген бір ауданның, қандай да болсын бір осьі арқылы айналып құрылады
Айналу дене түсінігі

Мысал
1) Өмірдегі, қоладныстағы айналу денелерін есімізге түсірейік:

Цилиндр
Цилиндр - дегеніміз ол тіктөртбұрыштың бір осьнан айналу арқылы пайда болған кеңістіктегі геометриялық фигура.
Үстіңгі және астыңғы шеңберлер табан болып табылады
Екі шеңбер центрінен отетін түзу - цилиндр осі деп аталады.
Табан радиусы - цилиндр радиусы болып табылады.
Цилиндр биіктігі - екі шеңбер арасындағы кашықтык.

Айналу денелерінің ауданы мен көлемін табу формулалары

Есептер
1) Егер екі цилиндрдың осьтық қималары тең болса, биіктіктері тең болама?
жауап: жок
Sқима=2R·h
h
Осы тіктөртбұрыштың төменгі жағында айналғанда алынған дене бетінің ауданын табыңыз. Осы тіктөртбұрыштың төменгі жағында айналғанда алынған дене бетінің ауданын табыңыз.
5 см
R=5 см, h=4см
Sжалпы =2R(h +R) = 2· 5 ·(4 + 5) =90
Жауабы: жалпы ауданы 90 см2
h
2R
2R
S қима=h·2R
4 см
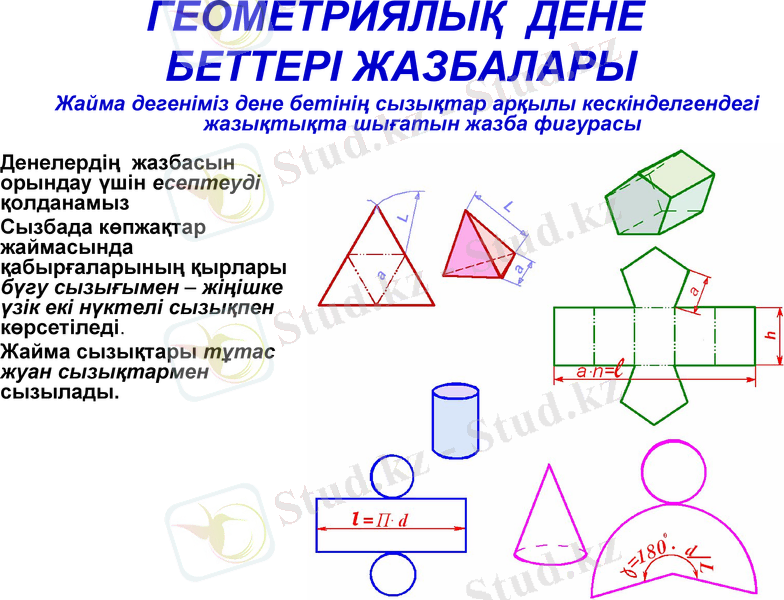
Геометриялық дене беттері жазбалары
Денелердің жазбасын орындау үшін есептеуді қолданамыз
Сызбада көпжақтар жаймасында қабырғаларының қырлары бүгу сызығымен - жіңішке үзік екі нүктелі сызықпен көрсетіледі.
Жайма сызықтары тұтас жуан сызықтармен сызылады.
Жайма дегеніміз дене бетінің сызықтар арқылы кескінделгендегі жазықтықта шығатын жазба фигурасы
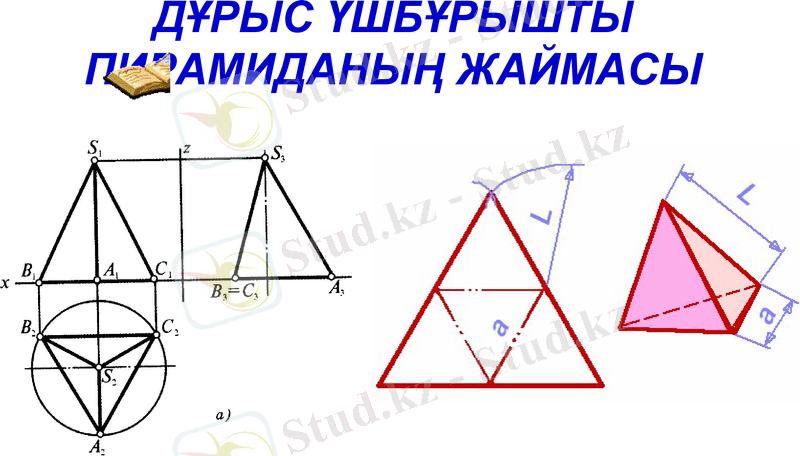
Дұрыс үшбұрышты пирамиданың жаймасы
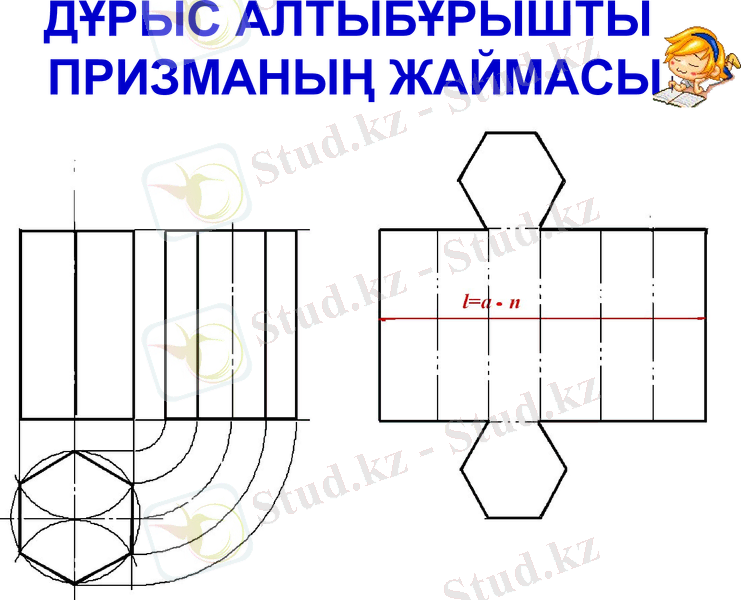
Дұрыс алтыбұрышты призманың жаймасы
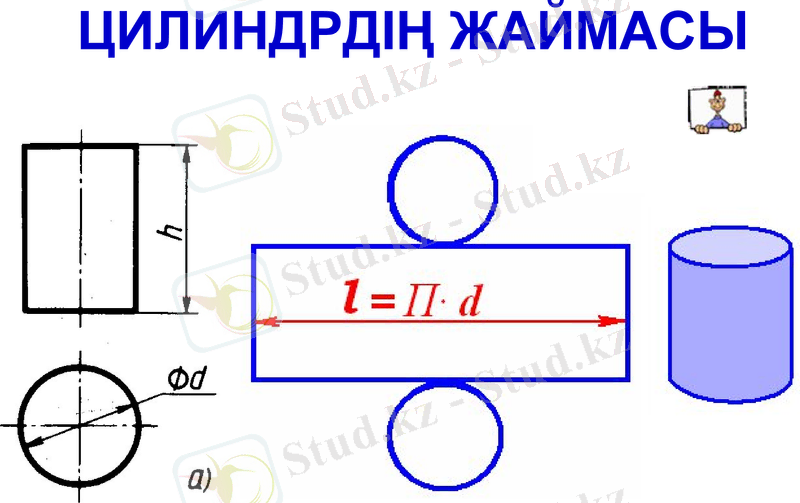
Цилиндрдің жаймасы
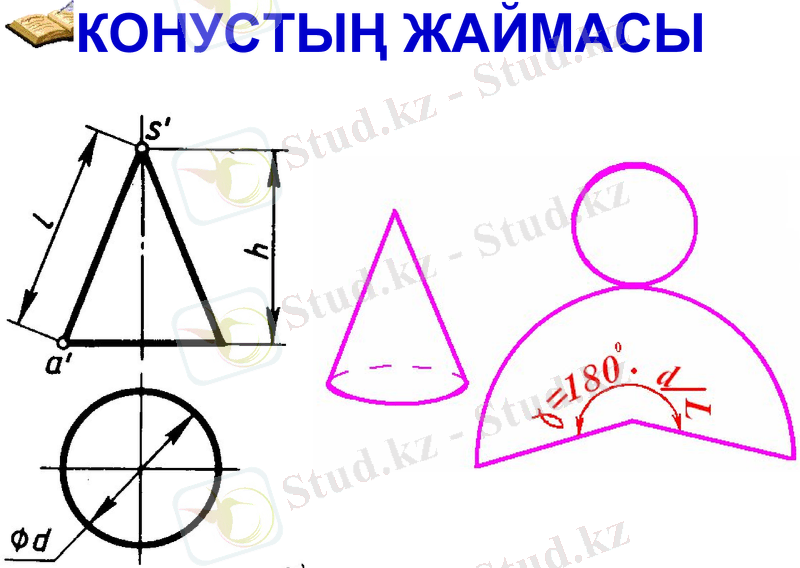
Конустың жаймасы

Тапсырмалар А4 форматтарына геометриялық дененің екі көрінісін және жаймасын сызыңыздар.
Табанына сырттай сызылған шеңбердің диаметрі 35 мм, биіктігі 45 мм болатын дұрыс төртбұрышты пирамиданың жаймасын орында.
2. Табаны фронталь жазықтығында жатқан диаметрі 30 мм, биіктігі 35 мм цилиндрдің екі проекциясын және жаймасын сыз.
3. Табанының диаметрі 30 мм, биіктігі 40 мм конустың сызбасы мен жаймасын орында.

Назарларыңызға рахмет!
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz